7.Похідні за напрямками. Градієнт ф-ї декількох змінних.

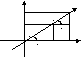
Нехай в обл. Д задано f(х;у) і точку М_о(х_о;у_о).

Проведемо із т. М_о вектор ℓ під кутом a до ОХ.

На ℓ візьмемо т. М(х,у). Тоді / ММ_о/=f(М)-f(М_о)=((х-х_о)²+ (у-у_о)²)^0,5=(∆х²+∆у²).

Припустимо, що ф-я f(х;у) неперервна і має непер. похідні по своїм аргументам. Тоді повний приріст ф-ї можна записати у вигляді:

∆Z=(∂z) ∆х+(∂z )∆у+a₁∆х+a₂∆у

(∂х ) (∂у)

Поділимо ліву і праву частину на ∆ℓ.

Похідною ф-ї Z=(х;у) в напрямком ℓ в т.М₀ наз границя відношення ∆Z до ∆ℓ коли останне прямує до 0.Таким чином похідна за напрямком:

∂Z М₀= ∂Z М₀ соsa+∂Z М₀ sіna

∂ℓ ∂х ∂у

Із всіх напрямків що, виходять з т М₀ , необхідно знайти такий в напрямку якого , похідна aZ/∂ℓ приймає найб значення. Це напрямок градієнта.

Градієнтом ф-ї Z=f(х;у) в т М_о(х_о;у_о) наз вектор з початком в т М_о, який має своїми координатами частинні похідні ф-ї Z.

_{grad Z =(}∂Z/∂х)/ М₀^і_{+ (}∂Z/∂у)/ М₀^j.

Градієнт вказує напрям найб зростання ф-ї в даній точці. Похідна ф-ї в напрямку градієнта має найб значення.

_{grad Z =((}∂Z/∂х)²/ _{+ (}∂Z/∂у)²)^0,5

8. Метод найменших квадратів

В основі застосування методу найменших квадратів покладено умову мінімізації суми квадратів відхилень вибіркових даних від тих, що визначаються оцінкою.

Згідно з умовою мінімізації можна записати

u = £ (x, - її)¹ = min.

Для визначення екстремуму першу похідну функції u слід прирівняти нулю

-^dU- = -l£ (x,-//) = 0, звідки X ^(xi = Х ^x, - ⁿ<" = ⁰ і М= - Z x_t .

^dM ¡=1 i=1 i=1 ⁿ ,=1

Отже, /} _янк = x. 

Таким чином, оцінка за методом найменших квадратів математичного сподівання /й_янк випадкової величини x є вибіркове середнє x

9.Поняття про подвійні інтеграли та методи їх обчислення.

z = f(x,y) визначена в замкненій обмеженій області . Вважатимемо, що межа області D складається із скінченного числа неперервних кривих, кожна з яких визначається функцією виду y = f(x) або .

Розіб'ємо область D на n частин D_i, які не мають спільних внутрішніх точок і площі яких рівні ΔS_i, і=1, 2, ..., n. У кожній області D_i візьмемо довільну точку P_i(ξ_i,η_i) і утворимо суму

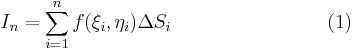
яку назвемо інтегральною сумою для функції z=f(x,y) по області D.

Нехай  - найбільший з діаметрів областей D_i.

Якщо інтегральна сума (1) при  має скінченну границю, яка не залежить ні від способу розбиття областей D_i, ні від вибору точок P_i(ξ_i,η_i), то ця границя називається подвійним інтегралом і позначається  або 

10. Диференціальні рівняння. Основні поняття і означення. Задача Коші.

Звичайним диф. рівнянням наз. р-ня, яке містить незал. змінну х,шукану ф-ю y=y(x) та похідну шуканої ф-ї до деякого порядку включно. Загальний вигляд: F(x,y,y’,y’’….y⁽ⁿ⁾)=0.

Порядком диф. р-ня наз. найвищий порядок похідної,що входить в дане р-ня.

y’+xy=0(диф.р-ня першого порядку); y’’+2y’+4y=sinx(диф.р-ня 2-гопорядку).

Рішенням диф.р-ня наз. всяка ф-я y=j(x),яка при підстановці в дане р-ня перетв.його в тотожність, тобто F(x, j(x), j’(x), j’’(x)… j⁽ⁿ⁾(x))=0.

Загальним розв’язком диф. р-ня n-го порядку наз. р-ня аргумента x і n довільних констант c₁,c₂…..c_n,тобто y=j(x, c₁,c₂…..c_n) при підстановці якої в дане р-ня одержуємо тотожність.

Частинним розв’язком диф. р-ня любого порядку наз.таке рішення р-ня, яке одержано із загального при фіксованих значеннях const, тобто:y= j(x, c₁⁰,c₂⁰,….c_n⁰),де c₁⁰,c₂⁰,….c_n⁰-конкретні числа.y=c₁e^x+c₂xe^x- загальне р-ня. Так, якщо y=c₁e^x+c₂xe^x –заг.розв’язок диф.р-ня,то якщо с₁=0,а с₂=1,то y^--=xe^x частинний розв’язок р-ня. Щоб одержати частинний розв’язок із загального, вводять додаткові умови, які наз. початковими умовами диф. р-ня.

Загальний вигляд початкових умов для:а) диф. р-ня 1-го порядку:y(x₀)=y_0. б) для 2-го порядку: y(x₀)=y_0, y’(x₀)=y’_0. Знаходження частинного розв’язку диф. р-няпо заданим початковим умовам наз. задачею Коші. Теорема про існування і єдність розв’язку задачі Коші завжди мають розв’язок і притому єдиний,зокрема для р-ня 1-го порядку. Якщо права частина р-ня y’=f(x,y) як ф-я двох змінних визначена і неперервна в обл..Д, що містить т.М₀(x₀,y₀) і має неперервні частинні похідні f’_x, f’_y в цій точні, причому f’_y≠0.

11.Диф. р-ня 1-го порядку з відокремленими змінними.

F(x,y,y’)=0 –диф.р-ня 1-го порядку в заг.вигляді. y’=f(x,y). Якщо права частина р-ня y’=f(x,y) може бути представлена у вигляді добутку двох співмножників,один із яких не містить змінної х,а другий не містить змінної у,то f(x,y)= f₁(x)f₂(у),тоді р-ня y’=f(x,y) набуде вигляду: y’= f₁(x)f₂(у), яке наз. диф. р-ням з відокремленими змінними. Метод розв’язанні: відокремлення змінних з наступним інтегруванням. у’=dy/dx,dy/dx= f₁(x)f₂(у) | x dx/ f₂(у). dy/ f₂(у)= f₁(у)dx. ∫ dy/ f₂(у)=∫ f₁(x)dx +c₁-загальний розв’язок р-ня y’= f₁(x)f₂(у).

Заув. Якщо загальний розв’язок одержимо у вигляду наявноє ф-ї, то його наз. загальним інтегралом.

Однорідні диф. р-ня 1-го порядку.

Р-ня 1-го порядку y’=f(x,y) наз. однорідним, якщо f(x,y) є однорідною ф-єю нульового виміру. Ф-я f(x,y) наз. однорідною ф-єю нульового виміру, якщо при множенні змінних х та у на параметр t значення ф-ї не змін, тобто: f(tx,ty)=f(x,y).Однорідна ф-я нульового виміру завжди може бути представлена у вигляді f(x,y)= j(у/х).Таким чином, однор. диф. р-ня можна записати у вигляді: y’= j(у/х).Метод розв’язку: підстановка: z=y/x; z=z(x); Знайдемо, y=xz,y’=z+xz’. Підставимо у і у’ в р-ня y’= j(у/х). Маємо: z+xz’=j(z). xz’=j(z)-z

z’=dz/dx,звідси, xdz/dx==j(z)-z. | * dx/x(j(z)-z). ∫dz/(j(z)-z=∫dx/x=ln|x|+c,c=const.

Якщо в цьому виразі замінити z=y/x, то одержимо загальний інтеграл р-ня y’= j(у/х).

Лінійні диф. р-ня 1-го порядку.

Диф. р-ня 1-го порядку назв. лінійним, якщо воно містить шукану ф-ю у, її похідну y’ і не містить їх добутку уу’. Загальний вигляд р-ня: y’+P(X)y=Q(x),де P(x),Q(X)- неперервні ф-ї від х. або деякі константи.Метод розв’язку: підстановка y=UV,U=U(X),V=V(X),тоді y’=U’V+UV’. Значення у і у’ підставляємо в y’+P(X)y=Q(x). U’V+UV’+P(x)UV=Q(X). Нехай U’V+ P(x)UV=0,тоді UV’= Q(x).Розв’яжемо р-ня U’V+ P(x)UV=0. V(U’+P(X)U)=0. U’= - P(X)U, U’=dU/dx; dU/dx= - p(x)U. ∫dU/U = -∫p(x)dx. ln|U| = -∫p(x)dx. U=e^-∫p(x)dx. Розв’яжемо р-ня UV’= Q(x). V’=Q(X)/U=Q(X)/ e^-∫p(x)dx=Q(X) e^-∫p(x)dx, V’=dV/dx. ∫dV=

∫Q(x) e^-∫p(x)dx .Отже, V=∫Q(x) e^-∫p(x)dx +c. y=UV= e^-∫p(x)dx (∫Q(x) e^-∫p(x)dx +c)-загальний розв’язок диф. р-ня.

Рівняння Бернулі.

Деякі диференціальні рівняння, які не є лінійними можуть бути зведені до лінійних після попередніх перетворень. До таких рівнянь відносять рівняння Бернулі.: у’+р(х)у=Q(х)+уⁿ, де р(х), Q(х)-деякі функції, що залежать від аргумента х, де n не дорівнює 0, n не дорівнює 1.

1. При n=1 одержимо рівняння: у’+р(х)у=Q(х)у; у’= (Q(х)- р(х))у

2. При n=0, у’+р(х)у=Q(х) – лінійне диференціальне рівняння І порядку.

3. n не дорівнює 1, n не дорівнює 0 : у’+р(х)у=Q(х)+уⁿ – рівняння Бернулі.

За допомогою підстановки:

Z=y^1-n дане рівняння зводиться до лінійного і далі розв’язується як лінійне рівняння.

Поділимо рівняння на уⁿ:

у’+р(х)у=Q(х)+уⁿ| : уⁿ; у’/ уⁿ+ р(х)у / уⁿ= Q(х)уⁿ / уⁿ; у’/ уⁿ+ р(х)у^1-n = Q(х) вводимо заміну: Z=y^1-n.

(1-n) у ^–n * у’ = Z’;

(1-n) у’/ уⁿ= Z’; у’/ уⁿ= Z’/(1-n). Тоді рівняння у’/ уⁿ+ р(х)у^1-n = Q(х) можна переписати у вигляді: Z’/(1-n)+ р(х) Z= Q(х). Одержали лінійне диференціальне рівняння І порядку. Зауважимо, що рівняння Бернулі може бути розв’язане як лінійне без попереднього зведення до лінійного.

12. Диференціальні рівняння 2-го порядку. Інтегрування найпростіших типів рівнянь 2-го пор., які допускають пониження порядку у^,,=f(x); у^,,=f(x, y^,); у^,,=f(y, y^,)

Диф.р-ня 2-го пор. має вигляд F(x,y,y^,,y^,,)=0(1). якщо дане рівняння розв’язати відносно похідної 2-го пор., то одержимо р-ня у^,,=f(x,y,y^,,)(2).

Загальним розв. диф. р-ня 2-го пор.(1) або (2) наз.ф-я y=φ(x, C_1,C₂), C_1,C₂-const, яка при любих знач. довільних C_1,C₂ обертає дане р-ня в тотожність.

Частинним розв’язком диф. р-ня 2-го пор. наз. ф-ю ^,=φ(x, C₁⁰_,C₂⁰), де C₁⁰_,C₂⁰- конкретні значення. Частинний розвязок одержують із загального за допомогою початкових умов y(x₀)=y₀, y^,( x₀)=y₀.Початкові умови задовольняють значення C_1,C_2.

Теорема про існування і єдність розвязку. Якщо ф-я f(x, y, y^,) як ф-я трьох незалежних змінний змінних x, y, y^, неперервна в обл., що містить т. М₀(x, y, y^,), то диф р-ня у^,,=f(x ,y, y^,), y =φ(x) має розв. y(x₀)=y₀, y^,( x₀)=y₀^,. І крім того , якщо частинні пох. неперервні, то розв. єдиний.

Р-ня у^,,=f(x)(3) не містить y,y^,.Відомо, що y^,=y_x^,,тоді y^’’=(y^’)^’,y^’’=,^x, ,,, де С-const.,,,,, C_1,C_2.-const.Заг розв. р-ня (3) знаходиться двократним інтегруванням р-ня(3).

у^,,=f(x, y^,)(4)-не містить у.Щоб розв’язати р-ня(4) покладемо ,де z=z(x), тоді y^’’=z^’.z^’=f(x,z)- р-ня 1-го порядку.З цього р-ня знайдемо z=φ(x,C₁), z=y^’.-----загальний розвязок р-ня (4).

у^,,=f(y, y^,)(5)-не містить х.Щоб розв’язати(5) покладемо у^’=z, z=z(y), тоді у^’’=z^’y^’=z^’z,тоді (5) набуде вигляду z^’z=f(y,z)(6). Якщо z=φ(y,C₁)-заг розв р-ня(6), тоz= y^’ ,.------заг розв р-ня(5).