35. Неперервні випадкові величини. Інтегральна та диференціальна функції розподілу неперервної випадкової величини.

Неперервною в.в. назив в.в. , яка приймає всі значення з деякого скінченного або нескінченного інтервалу. До неперервних в.в. можно віднести помилки обчислень , температуру тіла людини та ін.

Н.в.в. можно задати 2-ма способами :

1) функцією розподілу F(x)

2)щільністю розподілу імовірностей f(x)

Неперервну випадкову величину можна задати за допомогою диференціальної функції розподілу.

Диференціальною функцією розподілу (позначається називається перша похідна від інтегральної функції розподілу, тобто

 .

Диференціальна функція визначає щільність розподілу ймовірності для кожної точки x і має перелічені нижче властивості.

Властивості диференціальної функції розподіл

1. Диференціальна функція розподілу невід’ємна.

2. Невластивий інтеграл від диференціальної функції розподілу в межах від –¥ до +¥ дорівнює одиниці, тобто

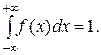
Знаючи вигляд диференціальної функції  , можна знайти інтегральну функцію  за такою формулою:

36. Числові характеристики неперервної випадкової величини

Дуже важливими в теорії імовірностей є окремі числові параметри, що характеризують істотні риси розподілу випадкових величин: математичне сподівання, що є деяким середнім значенням, навколо якого ґрунтуються можливі значення випадкової величини; дисперсія і середнє квадратичне відхилення, які характеризують ступінь розсіювання випадкових величин в околі математичного сподівання.

Математичним сподіванням дискретної випадкової величини називається сума парних добутків всіх можливих значень випадкової величини на відповідні їм імовірності:

=

Дисперсія випадкової величини є математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання.

Середнє квадратичне відхилення  є характеристикою розсіювання (the characteristic scattering) в. в. x; розмірність  збігається з розмірністю в. в.

Модою НВВ Х називають її можливе значення Яке визначається рівністю

37. Приклади законів розподілу неперервних випадкових величин: рівномірний, показниковий,нормальний розподіл.

Рівномірний закон розподілу

Якщо ймовірність потрапляння випадкової величини на інтервал пропорційна до довжини інтервалу і не залежить від розташування інтервалу на осі, то вона має рівномірний закон розподілу. Щільність такого розподілу:

Рівномірний закон розподілу легко моделювати. За допомогою функціональних перетворень із величин, розподілених рівномірно, можна діставати величини з довільним законом розподілу. Числові характеристики розподілу:

Показниковий закон розподілу

Щільність розподілу випадкової величини, розподіленої за показниковим законом, задається формулою:

Випадкові величини з таким законом розподілу широко застосовуються в задачах з теорії надійності та теорії масового обслуговування. Числові характеристики:

Нормальний закон розподілу

Нормальний закон розподілу задається щільністю Параметри, які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини. Нормальний закон розподілу широко застосовується в математичній статистиці. Для обчислення ймовірності потрапляння випадкової величини, розподіленої нормально, на проміжок використовується функція Лапласа:

Часто застосовується також формула: