Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_2

.pdf

Скачиваний:

Добавлен:

19.02.2016

Размер:

9.73 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 256 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

3.4.9.

z = 2x3 + 3y 2 ,

= {(x, y)

1 ≤ x2 + y 2 ≤ 9} .

3.4.10.

z = x2 − 3y2 + 2xy − 4x + 4y,

= {(x, y)

x ≤ 2, y ≤ x + 1, y ≥ 0} .

3.4.11.

z = 2x2 − y2 − 3xy − x + 5y,

= {(x, y)

x ≥ 0, y ≥ 0, x + 2y ≤ 4}.

3.4.12.

z = x3 + y3 − 3xy 2 ,

= {(x, y)

x ≥ 0, y ≥ 0, x + y ≤ 10} .

3.4.13.

z = x2 + 3xy + 2y 2 ,

= {(x, y)

y ≤ 2,

x ≥ 0,

y ≥ x − 2} .

3.4.14.

z = x2 + 2y2 − 3x − 5y + xy,

= {(x, y)

x ≤ 2,

y ≤ 2, x + y ≥ 0}.

3.4.15.

z = x3 + 2y 2 − x ,

= {(x, y)

x2 + y 2 ≤ 16} .

3.4.16.

z = x2 − 2y2 + 4xy − 6x ,

= {(x, y)

y ≥ 0, x ≥ 0, x + y ≤ 3} .

3.4.17.

z = 3x2 + y3 + 4 ,

= {(x, y)

1 ≤ x2 + y 2 ≤ 9} .

3.4.18.

z = x4 − 2x2 y 2 + y3 ,

= {(x, y)

y ≥ x2 , y ≤ 4} .

3.4.19.

z = x3 + 3x2 y + y3 ,

= {(x, y)

− 3 ≤ x ≤ 3, − 5 ≤ y ≤ 5}.

3.4.20.

z = 2x2 − 5xy + y 2 ,

= {(x, y)

y ≥ −3,

x ≥ 0,

x + y ≤ 1} .

3.4.21.

z = 2x2 + y2 + 2xy − 6x − 4y,

= {(x, y)

x ≥ −1, y ≥ 0, x + y ≤ 3} .

3.4.22.z = 6xy − 9x2 − 9y 2 + 4x + 4y , D = {(x, y) 0 ≤ x ≤ 1, 0 ≤ y ≤ 2}.

3.4.23.z = 4x − 2y + x − y + 1, D = {(x, y) 12 ≤ x ≤ 3, 13 ≤ y ≤ 2} .

3.4.24.

z = 4x − 4y − x2 − y 2 ,

= {(x, y)

x + y ≤ 2, y ≥ 0,

x ≥ 0} .

3.4.25.

z = x2

+ xy − 2 ,

= {(x, y)

y ≥ 4x 2 − 4, y ≤ 0} .

3.4.26.

z = 3x2 + 3y 2 − 2x − 2y ,

= {(x, y)

x + y ≤ 1, x ≥ 0, y ≥ 0} .

3.4.27.

z = x2

+ 2xy − 10 ,

= {(x, y)

y ≤ 2,

y ≥ x2 − 2} .

3.4.28.

z = x2

+ 4xy − 2y 2 − 6x ,

{(x, y)

x ≤ 0, y ≥ 0,

y ≤ x + 3} .

3.4.29.z = 5x2 − 3xy + y 2 , D = {(x, y) 0 ≤ x ≤ 2, 0 ≤ y ≤ 2} .

3.4.30.z = x2 + 2xy − 1, D = {(x, y) y ≤ 0, y ≥ x2 − 4} .

3.29.	arctg	1, 03	.	2.3.30. ((1,96)4 − (1,92)4 )2 .
		0, 98

http://vk.com/studentu_tk, http://studentu.tk/

Topic 4. Cоmplex Numbers

Concept of the complex numbers. The algebra of complex numbers. The geometry of addition and multiplication. The following section obtains the equation eiφ = cosφ + isinφ, thus giving a major application of complex numbers in the series and demonstrating the connection between the

exponential and trigonometric functions.

Literature: [2, section 1, р. 18––25], [3, ch. 7, §1], [4, §3], [5, ch. 3, §6], [6, section 7, ch. 7, §1––§8], [8, 1 part, ch. 6].

Т.4 Main concepts

4.1. Definitions

By a complex number, z, we shall mean an expression of the form

z = a + bi

where а and b are real numbers and i is the imaginary unit such that i2 = - 1. The form a + bi is called the rectangle form of the complex number. The number а is called the real part of z and b is called the imaginary part. One writes

a = Re z and b = Im z.

A better name for this set of numbers would have been the complete number system because this is the last extension that needs to be made to contain the roots of all polynomial equations.

If should seem reasonable that any real number is also a complex number. For example, consider the real number 7. If we express this number as 7+0i, we can see that it is qualified as a complex number.

Given a complex number z1 = a1 +b1i , the complex conjugate of z1 is

z 2 = a2 +b2i .

A complex number z = a +bi is equal to zero if and only a =b = 0 .

4.2. The algebra of complex numbers

Equality, addition, and multiplication of complex numbers are defined in a natural way. The multiplication of complex numbers is very much like that of polynomials, with one exception. When the quantity i2 occurs, it can be replaced by -1. Specifically: a+b i = c+di if and only a = c and b = d.

(a+bi) + (c+di) = (a+c) + (b+d); (a+bi)(c+di) = (ac - bd) + (ad+bc)i.

http://vk.com/studentu_tk, http://studentu.tk/

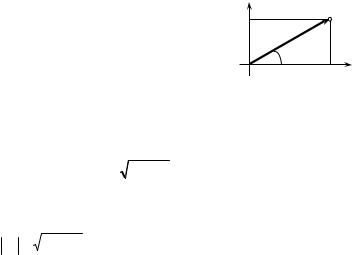
Example. Compute

1+ 4i .

2 + 3i

Solution. To divide, “conjugate denominator”:

1+ 4i

2 − 3i

2 − 3i + 8i + 12

14 + 5i

4 − 9i2

4 + 9

2 + 3i 2 − 3i

4.3. Complex numbers in trigonometric form

A complex number z = a+bi is completely determined by the real numbers a and b, there is a correspondence a+bi ↔ (a, b) between complex numbers and ordered pairs of real numbers. Specifically, for each complex number there corresponds a unique ordered pair of real numbers, and for each ordered pair of

real numbers there corresponds a unique complex	y
number. This suggests that we can represent	y	М
complex numbers geometrically in coordinate plane	b	ρ
as a point or as a radius-vector, called the complex		ρ
plane or the Gaussian plane (after Karl F. Gauss).		φ
The horizontal x-axis is called the real axis, which is		φ
The horizontal x-axis is called the real axis, which is	О	а x
simply the real number line. It is customary orien-	О	а x
tation. The vertical y-axis is called the imaginary		Fig. 1.18
axis. The graph of a complex number z = a+bi is
shown in fig. 1.18.

The absolute value of a complex number, called the modulus or magnitude of z and is defined by the Pythagorean Theorem, as shown in fig. 1.18.

z	= a2 + b2	(1.15)
z	= a2 + b2	(1.15)

Let φ be the angle in standard position whose terminal side is the vector OM representing z. If we let r be the magnitude of the vector OM , then

r = z = a2 + b2 and cos φ =		a	, sin φ =	b	and tan φ =	b	.
				r
		r				a
Therefore, we can substitute a =r cos φ and b = r sin φ in z = a + bi to
obtain
	z = a + bi = r (cos φ + i sin φ).					(1.16)

The form (1.16) is called the trigonometric form of the complex number. Sometimes the abbreviation r (cos φ + i sin φ) = r cis φ is used.

Each complex number z other than the origin can be written in polar coordinates as z = (r, φ), where r is positive and φ is determined up to an integer multiple of 2π.

The angle φ is called the argument of z and is written φ = arg z.

The trigonometric representation is not unique. In fact, there are an infinite number of trigonometric representation for a complex number because if φ is an argument of z, then so is φ + 2πk for any integer k. However, the representation

http://vk.com/studentu_tk, http://studentu.tk/

is unique for all nonzero z if 0 ≤ φ < 2π. Unique value of a complex number is obtained following the usual rules:

			b
			b
arctan				, if a >0,
arctan				, if a >0,

			a
			a

			b
			b	+π, if	a <0 and b > 0,
arctan
arctan
			a
			a

			b
arg z = arctan			b	−π, if	a <0 and b <0,	(1.17)
arg z = arctan				−π, if	a <0 and b <0,	(1.17)
			a
			a


π	, if a = 0 and b >0,
	, if a = 0 and b >0,

2

	π
	π	, if a = 0 and b <0.
−		, if a = 0 and b <0.
	2
	2

4.4. Multiplication and division in trigonometric form

The trigonometric form is quite effective when multiplying or dividing two complex numbers. Consider the product,

z1 z2 (r1 cis φ1)(r2 cis φ2) = r1(cos φ1 + i sin φ1) r2(cos φ2 + i sin φ2) = = r1 r2(cos φ1 cos φ2 –– sin φ1 sin φ2) + i (sin φ1 cos φ2+ sin φ2 cos φ1). Now use the addition identities for sine and cosine:

= r1 r2(cos (φ1 + φ2) + i (sin (φ1 + φ2) )= r1 r2 cis (φ1 + φ2).

Summary. In other words, to multiply two complex numbers in trigonometric form, multiply the moduli and add the arguments. A similar argument, left as an exercise, reveals, that to divide two complex numbers, divide the moduli and subtract the arguments

4.5. Raising a complex number to a power

For every natural n,

(r cis φ)n = rn cis nφ.

In other words
(r(cos φ + i sin φ))n = rn (cos nφ + i sin nφ).	(1.18)

The equation (1.18) is known as DeMoivre’s low.

For any positive integer n, the solutions to the equation (1.16) are given by

	1		n		ϕ + 2πk		ϕ + 2πk
z n		=				+ i sin			(1.19)
				r cos	n		n	.

For k = 0, 1, 2, 3,…, n – 1.

http://vk.com/studentu_tk, http://studentu.tk/

These solutions are called the nth roots of (1.16).

Furthermore, if m and n are positive integers,

	m			1	m
z	n	=		n
z		=	z		.

m

In other words, z n are the nth roots of z raised to the power m.

Let q be the rational number q = m/n or q = - m/n, where m and n are positive integers. If the trigonometric form of a complex number is

z = r(cos φ + i sin φ),

then

zq = rq (cos (q(φ + 2πk)) + i sin (q(φ + 2πk))), k = 1, 2, …, n – 1.

4.6. The relation between the exponential function and the trigonometric functions

With the aid of complex numbers, Euler in 1743 discovered that the trigonometric functions can be expressed in term of the exponential function ez, where z is complex. In particular, it will show that

iφ					eiϕ +e−iϕ					eiϕ −e−iϕ
e	= cos φ + i sin φ,		cos φ =				,	sin φ =			.
e	= cos φ + i sin φ,		cos φ =		2		,	sin φ =		2i	.
The hyperbolic function cosh x and sinh x were defined in terms of the
exponential function by
	cosh x =	ex	+ e− x	, sinh x =		ex		− e− x	.
	cosh x =		2	, sinh x =				2	.
If z = x + yi, the evaluation of ez			2					2
If z = x + yi, the evaluation of ez			can be carried out as follows:
	ez = ex + yi = ex(cos y + i sin y)

Summary. If

φ is a real number, then

z = a +bi = (r,ϕ) = r (cos ϕ +i sin ϕ)=

eiϕ .

The

The polar

The trigonometric

The polar

rectangular

form

Expression

eiφ

is called a power form of the complex number z.

Let z

=| z | eiϕ1 ,

=| z

| eiϕ 2

, then

1)z1 z2 =| z1 | | z2 | ei(ϕ1+ϕ2 ) ;

2)z1 = | z1 | ei(ϕ1−ϕ2 ); z2 | z2 |

3) zn =| z |n einϕ .

http://vk.com/studentu_tk, http://studentu.tk/

Т.4

Typical problems

1. Let

z1 =3+i , z2 = 4−3i . Evaluate:

а)

z +z

;

б) 3z −2z

;

в) z z

;

г)

;

д) (z )3 .

Solution. а) z1 +z2 = (3+i) +(4−3i) = 7−2i ;

б) 3z1 −2z2 =3(3+i)−2(4−3i) = 9 +3i −8+6i =1+9i ;

в) z z

= (3+i)(4−3i) =12 +4i −9i −3i2 =12−5i +3 =15−5i ;

3+i

(3+i)(4 +3i)

12 +4i +9i +3i2

г)

4−3i

(4−3i)(4 +3i)

16−9i2

9 +13i

i ;

д) (z )3 = (3+i)3	= 27 +27i +9i2	+i3 = 27 +27i −9−i =18+26i .
1
2. Determine. i18	+i25 +i36 +i−1 .
Solution. Use the fact that i2 =−1,		i3 =−i, i4 =1, then

i18 +i25 +i36 +i−1 = i16+2 +i24+1 +i36 −i =

=(i4 )4 i2 +(i4 )6 i +(i4 )9 −i = i2 +i +1−i = 0 .

3.Find the real and the imaginary parts of a complex number

z =

(3−2i)2

+(i −1)3 .

2i +1

Solution. Make a transformation

z =

9−12i +4i2

+i3

−3i2 +3i −1=

5−12i

−i +3+3i −1=

2i +1

(5−12i)(2i −1)

+2i +2 =

10i +24−5 +12i

+2i +2 =

12i +9

(2i +1)(2i −1)

−5

Hence,

Re z =−

, Im z =−

4. Find the moduli and the arguments of the following complex numbers. Write in trigonometric form:

a) z1 = 3 ; b) z2 = 2i ;	c) z3 =−1;
d) z4 =1+i ; e) z5 =1−i 3 ;
f) z6 =−2−i .
	56

http://vk.com/studentu_tk, http://studentu.tk/

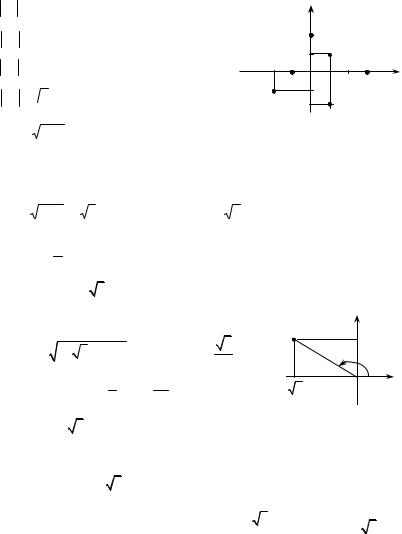
Solution. Fig. 1.19 shows all the complex numbers (See points M1 – M6). By the formulas (1.15) –– (1.17), the solutions are:

a)z1 = 3, φ = 0, z1 = 3(cos 0 + i sin 0);

b)z2 = 2, φ = π2 , z1 = 2(cos π2 +i sin π2 );

c)z3 = 1, φ = π; z1 = cos π + i sin π);

d)z4 = 2 , φ= π4 , z1=2(cos π4 +i sin π4 );

	y	М2
	2	М2	М4
			М4	М1
	М3			М1
–2	О	–1	1	3	х
М6		–1	М5
М6

1+ 3 = 2, φ=arctan( ––3) =

;

Fig. 1.19

=2(cos

;

−

+i sin −

4 + 1 =

5 , φ= arctan

−π , z6 =

5 (cos arctan

− π

isin arctan 12 − π .

5. Compute (− 3 +i)13 .

Express a complex number in trigonometric form (See fig. 1.20):

ρ = (− 3)2 +12 = 2 , cos ϕ =− 23 , sin ϕ = 12 , ϕ = 56π ,

М 1

− 3

5π

Fig. 1.20

z =−

3 +i = 2 cos

+i sin

Applying DeMoivre’s low gives

5π

(− 3 +i)

= 213

cos13

+i sin13

5π

cos 10π +

= 2

= 4096(− 3 +i).

+i sin 10π +

−

Find all solutions to

z4 +16 = 0 .

Solution. First write the equation in the form

z4 =−16 . Express number ––

16 in trigonometric form: −16 =16(cos π +i sin π) . 57

http://vk.com/studentu_tk, http://studentu.tk/

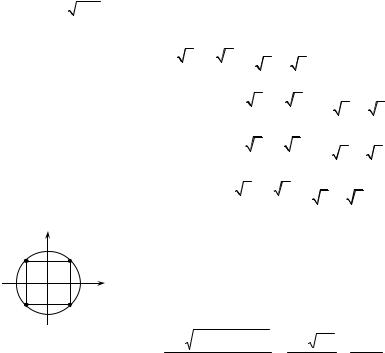
By the formula (1.5), we get

4 −16 =

π +2πk

+i sin

π +2πk

, k = 0, 1, 2, 3 .

2 cos

Then

= 2

cos

+i sin

2 +i

2 ,

π +2π

= 2

+i sin

= 2

−

=− 2

2 ,

cos

π +4π

= 2 cos

+i sin

= 2

−

−i

=− 2

−i

2 ,

π +6π

= 2

cos

+i sin

= 2

−i

2 −i

2 .

y			The graphs of these are shown in fig. 1.21. They are
			equally spaced along a circle of	radius 2. The angle
z2	z1
			successive root is 360° = 90°.

О	2	x	4	x2 −4x +5 = 0 .
			7. Solve the quadratic equation
z3	z4		Solution. By the quadratic formula, the solutions are

Fig. 1.21

x = 4 ± (−

1 5 = 4

± − 4 = 4 ± 2i = 2 ± i.

− 4

1,2

The solutions are 2 + i and 2 – i.

8. Let z = 2ei

=5ei

б) (z )6 .

6 , z

. Find: а)

z z

;

Solution.

а)

z1z2 = z1 =

= 6e

= 6 cos

+i sin

= 6i

;

iπ

б) (z )

= 64e

=−64 .

Exercises for class and homework

Т.4

Compute the given quantities:

2. (1−i)2 .

1. (2 +5i) +(2−2i) .

(3−4i)(3+4i) .

i +i11 +i21 +i31 +i41 .

5. (2−3i)(4−i) .

i i2 i3 i4 .

http://vk.com/studentu_tk, http://studentu.tk/

7.		1		+	1		.				8.		1 +i		.				9.	2 − 3i				.
		i3			i5									i						4 +5i
10.				2 + 3i					.		11.			(1−2i)(2 +i)				.	12.	3 − i			.
			(4 +i)(2−2i)												3 − 2i					3 + i
13.						3			3		14.	1					1		15.		1−i	3
13.	(1−i)						− (1	+i)		.	14.					+		.	15.			.
													1+2i				2−i
													1+2i				2−i			1+i

16.i5 +2 2 .i19 +1

In Problems 17 through 20, find the modules and arguments, graph in the complex plane, and express the complex numbers in trigonometric form.

17. z =−i . 18. z =1−i 3 . 19. z =− 3 +i . 20. z =−4 +4i .

Perform the indicated operations in Problems 21 through 23. Express answers in rectangular form.

21. (1+i)20 . 22. ( 3 + i)10 . 23. (5 2 (cos 6° +i sin 6°) )30 . Find all roots in Problems 26 through 30. Write answers in rectangular form.

24.	3 1 . 25. 4 −1 .	26. 3 i . 27. 4 cos 120°+i sin 120° .
Find all solutions to the equations in Problems 31 through 34.
28.	z3 +27 = 0 .	29. z4 −81= 0 .
30.	z6 +64 = 0 .	31. z4 +9z2 +20 = 0 .

Answers

	1.			4 +3i . 2. −2i .												3. 25.						4. i .		5. 5−14i . 6. ––1. 7. 0. 8. 1−i .															9. −	7	−	22	i .
	1.			4 +3i . 2. −2i .												3. 25.						4. i .		5. 5−14i . 6. ––1. 7. 0. 8. 1−i .															9. −		−	41	i .
																																							41			41
10.		1		+			21		i .		11.		18			−	1			i .		12.		0,5−0,5i						3 .	13. −4i .				14.		0, 6 −0, 2i .				15. i .
10.		68		+			68		i .		11.			13		−				i .		12.		0,5−0,5i						3 .	13. −4i .				14.		0, 6 −0, 2i .				15. i .
		68					68							13		13							5π					5π														π
																							5π					5π									π					π
16. −2 +1,5i .																		17. cos																					+ i sin
16. −2 +1,5i .																		17. cos							+i sin														+ i sin

																												6
																							6					6									3					3
					5π							5π											3π				3π
					5π							5π											3π				3π
19.	2 cos							+isin							. 20.				4(cos					+isin					) . 21. ––1024. 22.							512(1−i 3) .23. –64.
19.	2 cos							+isin							. 20.				4(cos					+isin					) . 21. ––1024. 22.							512(1−i 3) .23. –64.
						6																	4				4
						6						6											4				4
24. 1;								−		1	±i		3			.						25. ±			2	(1±i) .					26.		1	(	3 +i),			1	(− 3 +i), −i .
										2			2												2							2					2
			3												1																3
			3						1						1				3												3								29. ±3; ±3i .
27.																									28. –3,							(1±i			3) .
	±					+i					± −					+i
	±					+i				,	± −					+i					.
			2					2							2	2
			2					2							2	2															2
																															2
30. ±2i;						±(					3 +i);					±(				3 −i). 31. ±3i;										±i	5 .
																									59

http://vk.com/studentu_tk, http://studentu.tk/

1.1.2. z = 32i+−1i +(2i −1)3 .

Т.4	Individual tasks

1.1. Find the moduli and arguments of the following complex numbers.

1.1.1. z = i2+−2i +(i −1)4 .

1.1.3. z =

(2−i)3

+2i +3 .

1.1.4. z =

1−i5

(i +2)2

+1)5

1−i

2−3i

1.1.5. z =

−

1.1.6. z =

i +1 1−2i

1−i

1.1.7. z =

(1−i)(2 +3i)

+i12 .

1.1.8. z =

(2 +i)4

2i +1

(2i −1)(i +2)

1.1.9. z =

(4−i)(2i +1)

+i21 .

1.1.10. z =

(2−i)4

(2i −3)(i +4)

1.1.11. z =

(2 +i)(4 +5i)

+i32

. 1.1.12. z =

2−i

−

3−4i

2i −1

i +2 2−3i

(1−i)

2 +i

1.1.13. z =

1.1.14. z =

(3i −1)(i +3)

2−i

1.1.15. z =

4 +i

+(i −2)3 .

1.1.16. z =

(1−i3 )(2 +i)

4i −1

(i +2)4

1.1.17. z =

(1−i9 )(3+i)

1.1.18. z =

(4−i)(2 +5i)

+i51 .

(i −3)3

3i +1

1.1.19. z =

1+2i

2−i

1.1.20. z =

(1−2i)4

i +2

1−

(i +3)(3i +1)

(1+2i)

1.1.21. z =

3−i

−

1.1.22. z =

(i +4)(4i +1)

3+i

1.1.23. z =

(1+3i)(5−2i)

−i46

. 1.1.24. z =

3−2i

4−3i

2i +3

4i −1

2−i

(i −1)(2i +5)

1.1.25. z =

1.1.26. z =

1+2i

(3−i)

1−2i

1.1.27. z =

−2 +i +(3i −1)3 .

1.1.28. z =

(1+i11 )(2 +3i)

i −3

(2i −1)2

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 56 / 256 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.08.2019637.53 Кб4Gulenko.docx
#
12.11.2018765.44 Кб6Hagakure_-_Sokrytoe_v_listve.doc
#
19.02.20166.95 Mб201Higher Mathematics. Part 3.pdf
#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx