Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_2

.pdf

Скачиваний:

Добавлен:

19.02.2016

Размер:

9.73 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2516 17 18 19 20 21 22 23 24 25 > Следующая >>>

π 2

= t,

x = 2 arctg t,

∫0

2dt

cos x =

1− t2

2 + cos x

dx =

1+ t2

2dt

= ∫

1− t

0 (1+ t 2 )

1+ t

2∫

arctg

0 3

+ t

3 3 3

ln 5

e x

xe x − 1 dx.

10. ∫

+ 3

Solution. Let e x − 1 = t , the limits of integration with respect to t are: when

x = 0 we have α =

e0 − 1 = 0 and when x = ln5 t = β =

eln 5 − 1 = 2 .

Evaluate

2tdt

e x

= t 2 + 1 , e x dx = 2tdt ,

dx =

Then

t 2 + 1

ln 5

2 + 1) t

2tdt

t 2

t 2 +

− 4

∫

e x xe x −1dx = ∫

= 2∫

dt = 2∫

dt =

+ 4

+ 3

+ 4 t

+ 1

+ 4

2 = 4 − π .

= 2∫ (1−

)dt = 2(t − 2 arctg

)

+ 4

In Problems 11 to 13 apply integration by parts.

11. Evaluate I = ∫4 ln x dx.

Solution. We try

u = ln x and dv = dx . Then du =

and

−

v = ∫ x

2 dx = 2x 2 . Thus I = 2

x ln x

− ∫2

x = 4 ln 4 − 4

x 1 =

=4ln4 −8 + 4 = 4(ln4 − 1).

12. ∫2 x 2 sin xdx .

151

http://vk.com/studentu_tk, http://studentu.tk/

Solution. Apply integration by parts twice:

∫2

x 2 sin xdx =

u = x 2 ,

dv = sin xdx,

du = 2xdx,

= − cos x

u = x, dv = cos xdx,

= − x 2 cos x

+ 2

∫ x cos xdx = 2∫ x cos xdx =

du = dx, v = sin x

= 2x sin x

− 2

∫sin xdx = π + 2 cos x

= π − 2 .

13. ∫2 sin n xdx ( n is a natural number).

0
Solution.	π
	π
J n =	2 sin n	xdx =	u = sinn−1 x,	dv	= sin xdx,	=
	∫		du = (n − 1)sinn−2 xcos xdx,	v	= − cos x
	0
	0

= − cos x sin n−1 x

+ (n − 1)∫ cos2 x sin n−2 xdx =

= (n − 1)∫2

(1− sin 2 x) sin n−2 xdx = (n − 1)∫2 sin n−2 xdx − (n − 1)∫2 sin n xdx .

Thereby 0

J n = (n − 1)J n−2 − (n − 1)J n .

Thereafter

n − 1

J n =

J n−2 .

If n = 2k − 1 is an odd number, we get a recursion formula. Recall that

				π
			2					π
		J1 = ∫sin xdx = − cos x							= 1 .
		J1 = ∫sin xdx = − cos x						2	= 1 .
Then			0				0
Then		(2k − 2)!!				(2k − 2)(2k − 4)… 4 2				( k N ).
J 2k −1	=	(2k − 2)!!	=			(2k − 2)(2k − 4)… 4 2
J 2k −1	=	(2k − 1)!!	=			(2k − 1)(2k − 3)… 5 3
		(2k − 1)!!				(2k − 1)(2k − 3)… 5 3
					152

http://vk.com/studentu_tk, http://studentu.tk/

∫

If n = 2k

is an even number and recalling that

J 0 =

dx =

, we get a

recursion formula

J 2k

(2k − 1)!!

(2k − 1)(2k − 3)… 3 1

( k N ) .

(2k)!!

(2k)(2k − 2)… 4 2

Т.6 Exercises for class and homework

Evaluate the given definite integrals.

	16		x − 4 dx .
1.	∫		x − 4 dx .
	1		x + 2
	π 2					dx
4.	∫					dx				.
4.	∫		2 cos x + 3							.
	0
	4			x
7.	∫			x			dx .
	1		x +			1
	ln14			e	x		e	x	− 5
10.		∫		e			e		− 5		dx .
10.		∫				e	x	+ 1			dx .
	ln 5					e		+ 1
	ln 5

	a
13.	∫	a 2 − x 2 dx .
	0
	3	dx
16.	∫	dx	.
16.	∫	x x 2 + 5x + 1	.
	1	x x 2 + 5x + 1

e−2

19. ∫ ln(x + 2)dx .

2	2
2.	∫				x			x 2 + 1dx .
	0
	2		sin				1
	π						1
	π
5.	∫					x			dx .
5.	∫				x	2			dx .
	1				x
	π
	1
8.	∫ 1+xx dx .
	0
		− ln 2
11.					∫			1− e2x dx .
				0
	2								dx
14.			∫						dx			.
14.			∫									.
				2 x5						x 2 − 1
	1
17. ∫ xe− x dx .
	0
		π
20.		∫3			xdx						.
20.		∫3			2						.
		π sin								x
		4

	e	dx
3.	∫	dx	.
3.	∫		.
	1	x 1− ln 2 x
	2	dx
6.	∫	dx	.
6.	∫	x(x + 1)	.
	1	x(x + 1)
	1
	14	x
9.	∫	x	dx .
	2	2 + x

12. ∫ x 2 1− x 2 dx .

15. ∫ dx .

1 x + x3

18. ∫4 x cos 2xdx .

21. ∫ ln 2 xdx ;

153

http://vk.com/studentu_tk, http://studentu.tk/

Answers

1. 12.		2. 26 .		3.			π		. 4.		2 arctg		1	.		5. 1.			6. ln				4	. 7. 3.						8.	2 −	π	.	9.	88 .
		3					2				5	πa 2	5										3									2			3
11.	3	+ ln(2 −		3) .					12.	π	. 13.	πa 2	.	14.		1	(π +	7 3		− 8) .				15.			1	ln	8	.	16. ln			7 + 2 7		.
11.	2	+ ln(2 −		3) .					12.	16	. 13.	4	.	14.		32	(π +	2		− 8) .				15.			2	ln	5	.	16. ln			9		.
	2									16		4				32		2									2		5					9
17.1− 2/ e . 18.				π	−	1		. 19. 2 − 2ln 2 . 20.							π	(9 −4		3)+			1	ln			3	. 21. e − 2 .
						1
				8		4									36						2				2

			Т.6		Individual test problems

Use the substitution to evaluate the integrals.

293 (x − 2)2

1.∫3 3 + 3 (x − 2)2 dx .

8		x + 1 + 1 dx .
4. ∫
3		x + 1 − 1
ln 5		e x	xe x − 1 dx .
7. ∫
0		e	+ 3

4			dx
10. ∫						.

0	1 +		2x + 1
0.5ln 2			e x dx
13.		∫
								.
			x			− x
		0	e	+ e

2				dx
16. ∫						.

0		x +1 +				(x +1)3
5			x2 dx
19. ∫						.
2		(x − 1)			x − 1
ln 2			dx
22. ∫						.

0		e x	1 + e−2x
e3		ln xdx
25. ∫							.
					2
e	2 x(1 − ln					x)

13		(3x + 1)dx .
28. ∫
0		2x + 1

ln 2

∫

+ e

− x

)

∫

2x +

3x + 1

ln 2

∫

e x

− 1dx .

7 / 3

xdx .

11.

∫

2 / 3

3x + 2

14. ∫

x + 1

−11

xdx .

17. ∫

3x +

π / 2

cos xdx .

20.

∫

4 +

sin x

23. ∫

1 x

1 + ln x

x3dx

26.

∫

(1 + x

)

2 / 3

ln12

29.

∫

4 + e x

ln 5

154

8	xdx .
3. ∫	xdx .
3	x + 1

	2 ln 2				dx
6.		∫						.
6.		∫		e	x	−		.
	ln 2			e		−	1
	ln 2
	5		xdx .
9. ∫			xdx .
	0		x + 4
	ln 3				dx
12.	∫				dx				.
12.	∫		e	x	− e		− x		.
	ln 2		e		− e
	ln 2
	1		x2 dx
15. ∫			x2 dx				.
15. ∫			4				.
	0	(1 + x)
	0

∫x2 dx

18..7 3

0 9 + x

	0	x
21.	∫	1 − e	dx .
21.	∫	x	dx .
	ln 3	1 + e
	ln 3
	ln 3	dx
24.	∫	dx		.
24.	∫	1 + e x		.
	ln 2	1 + e x
	9	xdx .
27. ∫		xdx .
	4	x − 1
	1	xdx .
30. ∫		xdx .
	−1	5 − 4x

http://vk.com/studentu_tk, http://studentu.tk/

Topic 7. Improper integrals

Improper integrals: integral of integration unbounded and integrand unbounded. Definitions and evaluation. Convergent and divergent improper integrals.

Literature: [1, section 8], [3, term 7, § 2], [6, section 9, п. 9.4], [7, section 11, § 7], [9, § 40].

Т.7	Main concepts

7.1. Improper integrals: integral of integration unbounded

There is the first type of improper integral. Suppose f(x) is continuous and nonnegative for a ≤ x <∞ (see fig. 2.2).

We know that integral ∫b				f (x)dx is the area of		у
the region between			a		and the
the region between		the curve y = f(x)			and the		у=f(x)
x-axis from x = a to x = b. As b → ∞, we may							у=f(x)
x-axis from x = a to x = b. As b → ∞, we may
think of blim→∞ ∫b	f (x)dx	as the area of the unbounded

						О	а	b х
a	shaded		in fig. 2.2. This		limit is	О	а	b х
region that is	shaded		in fig. 2.2. This		limit is		Fig. 2.2
abbreviated by							Fig. 2.2
abbreviated by
	∞		(x)dx ,
	∫ f		(x)dx ,
		a
							∞
called the first type of improper integral. If this limit exists,							∫ f (x)dx	is said to

be convergent or to converge to that limit. In this case the unbounded region is

∞

considered to have a finite area, and this area is represented by ∫ f (x)dx . If the

limit does not exist, the improper integral is said to be divergent and the region does not have a finite area.

We can remove the restriction that f(x) ≥ 0. In general, the improper integral

∞

∫ f (x)dx is defined by

∞	A
∫	f (x)dx = Alim→ ∞ ∫ f (x)dx .
a	a
	155

http://vk.com/studentu_tk, http://studentu.tk/

b	∞
Other forms of improper integrals are ∫ f (x)dx and	∫ f (x)dx . In each of
−∞	−∞

three forms of improper integrals, the interval over which the integral is evaluated has infinite length.

The improper integral		∫b		f (x)dx is defined by
		−∞
			b	f (x)dx		= lim b		f (x)dx .
			∫				B →− ∞ ∫
			−∞				B
If this limit exists,		∫b	f (x)dx			is	said to	be convergent. Otherwise, it is
divergent.		−∞
divergent.
		∞			(x)dx is defined in erms:
The improper integral		∫ f			(x)dx is defined in erms:
		−∞
∞						c		A
∫	f (x)dx =				lim		f (x)dx + lim		f (x)dx ,
∫					B→−∞ ∫			A→∞ ∫
−∞						B		c

where c is the real number.

∞

If both integrals on the right side are convergent, then ∫ f (x)dx is said to be

−∞

convergent. Otherwise, it is divergent.

7.2. Improper integrals: integrand unbounded

There is a second type of improper integral, in which the function is unbounded in the interval [a, b] If the function f(x) becomes arbitrarily large in the interval [a, b], then it is possible to have arbitrarily large approximating sums

∑ f (ξi ) xi no matter how fine the partition may be by choosing a ζ1 that

i=1

makes f(ζ1) large.

Let f(x) be continuous at every number in [a, b] except a, and become

arbitrarily large for values in (a, b). If lim ∫ f (x)dx exists, the function f(x) is

ε→0 a+ε

said to have a convergent improper integral from a to b. The value of the limit is

b		b
denoted ∫ f (x)dx . If	ε→lim0	∫ f (x)dx does not exist, the function f(x) is said to
a		a+ε

have a divergent improper integral from a to b; in brief ∫b f (x)dx is not defined.

156

http://vk.com/studentu_tk, http://studentu.tk/

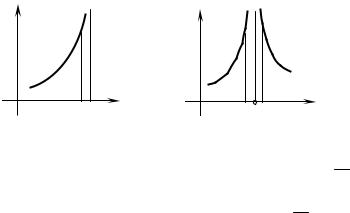
In a similar	manner, if f(x) is unbounded only near b (fig. 2.3), define
b	b − ε
∫ f (x)dx as limε→0	∫ f (x)dx .
a	a
It may happen that a function behaves well everywhere in the interval [a, b]

except at the number c, distinct from a to b (fig. 2.4), where it may be infinite. In

that case ∫b		f (x)dx makes		no sense. In		such a		case consider ∫c	f (x)dx and
	a							a
∫b	f (x)dx . If both exist, then the integral					∫b	f (x)dx	is said to be convergent and
c						a
have the value ∫c			f (x)dx +	∫b	f (x)dx . More generally, if a function f(x) has an
		a		c

infinite range of values as well as a point where it becomes infinite, break the entire integral into the sum of the integrals each of which has only one of the two basic “troubles”, either an infinite range or an endpoint where the function is

							∞
infinite. For		instance,		the	improper integral ∫			1	dx is troublesome for four
								x4
		1				1	−∞
reasons: lim			= ∞ ,	lim			= ∞ , and the range extends infinitely to the left
						x4
x→ 0	− 0 x4			x→ 0	+ 0

and also to the right. To treat the integral, write it as the sum of four improper integrals of the two basic types:

∞	−1	0	1	∞
∫ dxx4 =	∫ dxx4 + ∫ dxx4 + ∫ dxx4 + ∫ dxx4 .
− ∞	− ∞	−1	0	1
у			у
			у
у=f(x)			у=f(x)

О а	b–ε b х			b х

		О а c–ε c c+δ
	Fig. 2.3		Fig. 2.4

∞ dx

All four of the integrals on the right have to be convergent for −∫∞ x4 to be

∞ dx

convergent. As a matter of fact, only the first and last are. So −∫∞ x4 is divergent.

157

http://vk.com/studentu_tk, http://studentu.tk/

Just as substitution in a definite integral is valid as long as the same substitution is applied to the limits of integration, substitution in improper integrals is also permissible.

Т.7 Typical problems

In exercises 1 and 2 determine whether the improper integrals are convergent or divergent. Evaluate the convergent ones.

∞

1. ∫

1 + x

Solution. By definition

∞

∫

= lim

∫

lim arctg x

1 + x

1+ x

A→∞

= lim (arctg A − arctg1) =

−

∞

A→∞

Therefore, ∫

converges to

and the area in question is

1+ x2

∞

2. ∫

∞

Solution.

∫

= lim

∫

= lim ln

lim ln

=∞ .

1 x

A→∞

1 x

A→∞

Therefore, the given integral is divergent.

∞

3. Examine the improper integral ∫

for all p .

Solution. By example 2 if

p = 1 the integral is divergent. If p ≠ 1 , then

∞

− p+1

∫

= lim

∫

= lim

− p + 1

p − 1

A→∞

A→∞ − p + 1

p > 1,

p − 1

∞,

p < 1.

In exercises 4—5 determine whether the improper integrals are convergent or divergent. Evaluate the convergent ones.

158

http://vk.com/studentu_tk, http://studentu.tk/

∞

∫

− 6x

+ 10

−∞ x

Solution. The substitution x – 3 = t transforms the integral to

∞

−∫∞

By definition

t2 + 1

∞

∫

+ ∫

lim

∫

+ lim ∫

−∞ t

a t

+ 1

A→−∞ A t

+ 1

B→∞ a t

+ 1

where a is any number.

Thus:

arctg t

= arctg a −

arctg A = arctg a +

lim

∫

= lim

lim

;

A→−∞ A

A→−∞

Next consider

lim ∫

= lim arctg t

−arctg a .

Hence

B→∞ a t

B→∞

∞

∫

= π , namely

∫

is convergent and equals π.

−∞ t

+ 1

−∞ x

− 6x +

∞

5. ∫

ln x

dx .

∞ ln x dx

A ln xd (ln x) =

Solution.

= lim

lim

ln 2 x

= ∞ .

∫

A→∞

∫

A→∞

Therefore, the given integral is divergent.

In Exercises 6 to 8 examine the improper integral.

∞

6. ∫

cos x

dx .

cos x

Solution. The integrand

is the alternative function if x ≥ 1.

cos x

generally known

cos x

≤1 ,

then

≤

. By Exercise 3 the

∞

integral

∫

is convergent ( p = 3 > 1 ), so is the given integral.

159

http://vk.com/studentu_tk, http://studentu.tk/

∞	(ln(1+ x2 ) − 2 ln x)dx .
7. ∫	(ln(1+ x2 ) − 2 ln x)dx .
1
Solution. Write the integral in the form
	∞	1	+ x 2		∞		1
	∫ ln	1	+ x 2		∞		1
					dx = ∫ ln 1	+			dx .
			x	2	dx = ∫ ln 1	+	x	2	dx .
	1		x		1		x

∞

By Exercise 3 the integral

∫

is convergent ( p = 2 > 1). Recall also that

ln 1+

lim

= 1 , so is the given integral.

x→∞

∫

+ 2x − 3

Solution. At x = 1 the integrand is undefined, and near x = 1 it is unbounded.

It is necessary to examine the improper integral

d(x + 1)

∫

= lim

∫

= lim

∫

+ 2x − 3

2x − 3

− 4

ε→0

1+ε

ε→0

1+ε (x + 1)

= lim

x − 1

lim(ln

−ln

) =∞.

x + 3

+ε

ε→0

1+ε

ε→0

Therefore, the given integral is divergent.

9. Examine the improper integral ∫

for all λ .

Solution. At x = 0 the integrand is undefined, and near x = 0 it is unbounded.

It is necessary to examine the two improper integrals. If λ ≠ 1 , then

1 dx

x1−λ

ε1−λ

∫

= lim

−

ε →0 ∫

ε →0

1− λ

− λ 1− λ

ε→0 1

1−λ

, if

< 1,

− lim

= 1

− λ

ε →o

∞, if λ >

Next consider for λ = 1

dx = lim ln

∫

= lim

∫

= +∞ .

ε→0

160

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2516 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.08.2019637.53 Кб4Gulenko.docx
#
12.11.2018765.44 Кб6Hagakure_-_Sokrytoe_v_listve.doc
#
19.02.20166.95 Mб201Higher Mathematics. Part 3.pdf
#
19.02.20169 Mб95Higher_Mathematics_Part_1.pdf
#
19.02.20166.63 Mб1052Higher_Mathematics_Part_1.pdf
#
19.02.20169.73 Mб45Higher_Mathematics_Part_2.pdf
#
19.02.20167.48 Mб408Higher_Mathematics_Part_2.pdf
#
19.02.20167.31 Mб123Higher_Mathematics_Part_2.pdf
#
19.02.20169.11 Mб304Higher_Mathematics_Part_3.pdf
#
19.02.2016694.82 Кб11HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192.23 Кб1hjuj;f.docx