Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный авиационный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Higher_Mathematics_Part_2

.pdf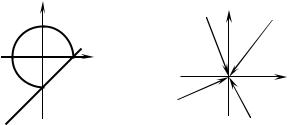

Скачиваний:

Добавлен:

19.02.2016

Размер:

10 Мб

Скачать

☆

<<< < Предыдущая 12 / 252 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

			lim (x2 + y2 ) arctg		x	= 0 .
			lim (x2 + y2 ) arctg		y	= 0 .
			x→0,		y
			y→0
4. Does lim		2xy		exist ?
4. Does lim	x2	+ xy + y 2		exist ?
x→0,	x2	+ xy + y 2
y→0

Solution. Let the point (x, y) approach (0; 0) along the line y = kx (fig. 1.7). Then

lim

2xy

lim

2x2 k

= lim

x→0, x2

+ xy + y 2

x→0 x2 + x2 k + x2 k2

x→0 1+ k + k2

+ k + k2

y→0

The values of an expression

are if change the slope k change.

1 + k + k 2

Hence, there are infinitely many diverse straight lines along which the point

(x, y) approaches (0; 0). Thus the limit does not exist.

y=k2x

y=k1x

2 х

–2

Рис. 1.7

Рис. 1.6

5. Calculate

lim

e x4

− e y4

x 2

− y 2

x→0,

y→0

Solution. Here

lim

e x4 − e y4

= lim

e y4 (e x4 − y4

− 1)

lim

e x4 − y4

−

x2 − y 2

− y 2

x→0,

→0,

x→0,

→0

y→0

x 4 − y 4 → 0

= lim

− y 4

= lim (x2 + y 2 ) = 0 .

e x4 − y4 − 1 ≈ x 4 − y 4

− y 2

x→0,

x + y

y→0

→0

6. Let f(x, y) =

, if

x − y ≠ 0, is f continuous at (0, 0) ?

x − y

x − y = 0.

http://vk.com/studentu_tk, http://studentu.tk/

Solution. Let’s consider			limit of f	along the y-axis. Since x = 0 and
lim	x + y	= −1 the limit at (0, 0) is not equal to the value of function at (0, 0):
lim	x − y
y→0	x − y
x=0,
–1 ≠ 0. Thus the limit is not continuous at (0, 0).
	7. Investigate for continuity.
			sin(x2 + y2 )
		f(x, y) =	x2 + y2	, if x2 + y2 ≠ 0,
		1,	if x = y = 0.

Solution. The given function is determined at all points of the xy-plane. Another,

lim

sin(x2 + y2 )

sin(x2

+ y2 ) ~ x2 + y2

= lim

x2 + y2

= 1 ,

x2 + y2

x→0,

y→0

→0

sin(x2

+ y2 )

sin(x2

+ y2 )

+ y2 ≠ 0 .

lim

for

x→ x0 , x2 + y2

x02 + y02

y→ y0

As (1.1) shows, function f (x, y) is continuity at any point of xy-plane.

Т.1 Self-test and class assignments

Find and graph the domain on the xy-plane of the following functions.

1.	z = ln(y − x2	+ 3x − 2) .	2.	z =	(x − 1)( y − x2 ) .
3.	z = arcsin(x2	+ 4y 2 ) .	4.	z = tg		πx	ctg πy .
3.	z = arcsin(x2	+ 4y 2 ) .	4.	z = tg	2		ctg πy .
					2
5.	z = (ln(5 − x2	− y 2 ))−1/ 2 .	6.	z =	x2 + y 2 − 1 +			1	.
								x2 − y 2

Find and graph the domain in the xyz-space of the following functions.

7.	u =	4 − x2 − y2 − z2 + x .
8.	u = 4 (x2 + y 2 − 1)(z 2 − 1) .

9.u = ln(1− x2 ) + ln(4 − y2 ) + ln(9 − z2 ) .

10.u = arccos x + arccos 2 y + arccos z 2 . Do the following limits exist? If so, evaluate them.

http://vk.com/studentu_tk, http://studentu.tk/

11.

lim

x + 2 y

12.

lim

4 + y

y→0 x + 6y

y→0

+ y

x→0,

14.

lim

arctg(xy)

. 15.

lim

tg(xy)

x2 + y 2

x→∞,

x→0,

xy2

y→∞

y→2

lim xe−(x2 + y2 ) .

17.

lim e

x2 + y2

18.

x→∞,

y→1

y→∞

Investigate for continuity.


13.	lim	sin(x + y)		.

	x→0,		x2 + y 2
	y→0
16.	lim		sin(x + 2y)		.

	x→∞,		2xy − 3
	y→1

19.	f (x, y) =	x2	+ y2	.	20. f (x, y) =		x2 + y 2	.
		x − y				x2	− xy + 2y 2

sin x +sin y

, if x + y ≠ 0,

x + y

21. f(x, y)=

1, if x + y = 0.

x y

, if

+ y

≠ 0,

+ y

22. f(x, y) = x

0, if x = x = 0.

Find the points or lines where z is not continuous.

23. z =	x + y	.	24. z =	x − y	.
				x3 + y3
	x2 + y2

25. z = sin(x + y) . sin( y − x)

Answers


1. Fig. 1.8.		2. Fig. 1.9. 3. Fig. 1.10. 11. Does not exist. 12. 0. 13. ∞ .				14. 0.
15.	1/ 2 .	16. 0. 17. 1. 18. 0. 19. Continuous at		all points, except	points	on line
у =	х. 20. Continuous at all points, except (0; 0). 21. Continuous				at all	points.
22.	Continuous		at all points. 23. (0; 0) is not continuous. 24. On line у = –х is not
continuous. 25.			There are the plural of straight lines	y = x + πn,n Z	where z is not

continuous.

http://vk.com/studentu_tk, http://studentu.tk/

у=х2–3х+2

у=х

1/2

х2+ 4у2=1

1 х

х=1

Fig. 1.8

Fig. 1.10

Fig. 1.9

Т.1	Individual test problems

1.1. Find and graph the domain on the x,y-plane of the following functions.

1.1.1. z = ln(x − y) arccos(x2 + y2 ) . 1.1.2. z = x2 − y 2 ln x .

1.1.3. z =	4−x2 − y2 ln(x − y) .
1.1.5. z =	x −	y +	1 − x2 − y 2 .
1.1.7. z = arccos		1	+ (4 − x 2 − y 2 )−1/ 2 .
1.1.7. z = arccos		xy	+ (4 − x 2 − y 2 )−1/ 2 .
		xy

1.1.9. z = ln(9−x2 − y2 ) ln(x2 −1) .

1.1.11. z = ln sin x + ln cos y .

1.1.13. z = arcsin	y	ln(2 −	x	) .

	x2

1.1.15. z = y − − x + ln(4− y2 ) .

1.1.17. z = 9 − x2 − y 2 arccos y .

1.1.19.	z = arcsin	x2	+ y 2	− yx .
1.1.19.	z = arcsin		4	− yx .
			4
1.1.21.	z = arccos	x2	+ y 2	+ arcsin ln x .
1.1.21.	z = arccos		e2	+ arcsin ln x .
			e2


1.1.4. z = arcsin			x	2 + y 2			.
1.1.4. z = arcsin				2x			.
				2x
1.1.6. z = arcsin				x
					.
			x − y		.
1.1.8. z =	9x 2	+		4 y 2 −		36		.
1.1.8. z =	36 − 4x 2 − 9 y 2							.
	36 − 4x 2 − 9 y 2

y−x2

1.1.10.z = ln(x + y −1) .

1.1.12.z = ln(sin x sin y) .

1.1.14.. z = 4 x2 + y2 −1 . 16−x2 − y2

1.1.16.

z = ln

+ y 2

+ 2y

1.1.18. z =

4−

ln sin πx .

1.1.20.

z =

ln(1−

)

arcsin x

1.1.22.

z = ln( y(9−x2 )) .

http://vk.com/studentu_tk, http://studentu.tk/

1.1.23. z = ln((x + y) ln( y − x)) .			1.1.24. z =	y −ln x	.

				x − y
1.1.25. z = tg πx ln(9−x2	− y2 ) .		1.1.26. z = ln(1 − xy) ln(x + y) .
2	x2 + y2
1.1.27. z = ctg πx +arccos		.	1.1.28. z = ln(x(1−x2 − y2 )) .
	2

1.1.29. z = ((x 2 + y 2 − 1)(x + y))1/ 2 .			1.1.30. z = (−ln(x2 + y2 ))1/ 2 .

Topic 2. Partial derivatives and differentials of a function of several variables

The partial and total changes and the partial derivatives of a function of two variables. The differential of a function of several variables. Applications of the differentials. The partial derivatives and the differentials of a function of more than two variables.

Literature: [2, section 1, § 1.2], [3, ch . 6, § 2], [4, section 6, § 16], [6, section 6, ch. 6.1], [7, section 8, §§5––12], [9, § 44].

Т.1	Main concepts

2.1. The partial and total changes of a function of several variables

Let z = f(x, y) by a function and M (x, y) D by a point on the region D.

The problem is to estimate the difference between f(x + x, y + y) and f(x, y), the lengths of the vertical segments shown in fig. 1.2. (For convenience, assume

that both function values are positive.) Denote the difference by f or z and is called the total change:

f = z = f(x + x, y + y) – f(x, y).

If only the x coordinate changes from x to x+ x and y is constant the difference of f, namely x, changes and is denoted by xf or xz:

x z = f (x + x, y) − f (x, y) . Likewise, if only the y coordinate changes:

y z = f (x, y + y) − f (x, y) .

http://vk.com/studentu_tk, http://studentu.tk/

The total change	z is a function of two variables x	and y , x z is a
function of one variable	x ; y z is a function of one variable	y . Therefore,
	z ≠ x z + y z .

2.2. Partial derivatives

Let f be a function of x and y. The graph of z = f(x, y) is a surface. Consider a point (x0, y0) in the xy plane. The graph of z = f(x, y) for (x, y) near (x0, y0) may look like the surface in fig 1.11. Let (x0, y0, f(x0, y0)) be a point on the surface directly above (x0, y0). The plane P through (x0, y0) perpendicular to the y axis meets the surface in a curve z = f(x, y0).

Tangent line

z = f(x, y0)

(x, y0, f(x, y0))

(x0, y, f(x0, y))

(x0, y0, f(x0, y0))

Fig. 1.11

To find the slope of the tangent line to this curve in the plane P at the point

(x0, y0, f(x0,

y0)), consider, as of function of one variable in [1]. This slope is

called the partial derivative of f with respect to x at (x0, y0) and is denoted

′

zx ,

′

, fx(x, y),

∂z

∂f

. In terms of limits,

f x

∂x

x z

f (x0 + x, y0 ) − f (x0 , y0 )

= lim

lim

x→0

Likewise

y z

f (x , y

+ y) − f (x , y )

z′

lim

= lim

0 0

y→0

is the partial derivative of f with respect to y at (x0, y0).

A quantity may depend on more than two variables. For instence, the volume of a box dependens on three variables: the length s, width n, and heigth h, V = snh.

http://vk.com/studentu_tk, http://studentu.tk/

Procedure to Find ∂∂xz and ∂∂yz

To find ∂∂xz , treat y as a constant and differentiate f with respect to x in the usual way.

To find ∂∂yz , treat x as a constant and differentiate f with respect to y in the usual way

The notions and notations of partial derivatives carry over to functions of more than two variables. If u = f (x1 , x2 ,…, xm ) , there are m first order partial

∂u

, …,

∂u

derivatives:

∂x

To find

∂u

, treat xi (i≠ k) as a constant and differentiate f with respect to xk

∂xk

in the usual way.

the

partial

derivatives

the

composite

function

To find

u = f (x1 , x2 ,…, xm ) ,

where

= xi (t1 , t2 ,…, tk ) ,

i =1, 2, …, m

use the

following formulas.

∂x1

∂x2

∂xm

∂u

+ …+

∂u

∂t

∂x

∂t

∂x

∂t

∂x

∂t

……… ……… ……… ……… ……… ……

∂u

∂x1

∂u

∂x2 + …+

∂u

∂xm

∂t

∂x

∂t

∂x

∂t

∂x

∂t

Likewise, if

z = f (u, v) , where u = u(x, y) , v = v(x, y) , then

∂z

∂z ∂u ∂z

∂v ∂z

∂z ∂u ∂z ∂v

(1.2)

∂x +

∂x ,

∂y +

∂y .

∂x

∂u

∂v

∂y

∂u

∂v

For a function z = f (u, v) , where

u = u(x) and

v = v(x) , there is only one

partial derivative with respect to

and is called the total derivative:

∂z

∂v dx

∂u dx

Whether function u(x1, x2 ,…, xm )

is given in the intermediate form:

F(x1 , x2 ,…, xm , u(x1 , x2 ,…, xm )) = 0 ,

http://vk.com/studentu_tk, http://studentu.tk/

moreover

∂F ≠ 0

the

partial

derivative is

found

according

the

following

formula:

∂u

∂F

∂u

= −

∂xi

, i = 1, 2, …, m .

∂F

∂xi

∂u

For instance, if F(x, y, z(x, y)) = 0 , hence

∂z

∂F

∂z

∂F

∂x

∂y

= −

≠ 0 .

(1.3)

∂x

∂y

∂F

∂z

Let z = f(x, y) have continuous partial derivatives

z′

and

Theorem

z′

for all points within some disk with center at the point

(x, y). Then z, which is the change f(x +

x, y +

y) - f(x, y), can be written

′

y + ε1

x + ε2

(1.4)

z = zx

x + zy

where ε1 and ε2 approach 0 as

x and y approach 0. (Both ε1 and ε2 are

functions of the four variables x, y,

x and

y.)

2.3. The differential

When

x and y are small, the quantities ε1

x and ε2

y, being the products

of small quantities, are usually negligible when compared with

z′

x and

z′

(if z′

x and z′

y are not 0). For this reason,

z′

x +

z′

y is often a good

estimate of

z when

x and

y are small. The similarity with the case of a

function of one variable suggests the following definition.

If z is a function of two variables, and x, y,

x and y are numbers, then the

function of the four variables x, y,

x and

y, given by

z′

x + z′

is called the differential of z at x, y,

x and y. It is denoted dz or df.

Thus

dz =

∂f

dx +

∂f

(1.5)

∂x

∂y

Though the differential dz is a function of the four variables x, y,

x and

it is usually applied only when

x and

y are small.

http://vk.com/studentu_tk, http://studentu.tk/

In the case of a function of one variable the differential dy represents the change in y along a tangent line to the graph of the function. In the case of a function of two variables it turns out that the differential dz represents the change in z along a “tangent plane” to the graph of a function.

By the formula (1.4):

z = dz + ε1 x + ε2 y.

Hence

z ≈ dz

f (x + x, y +

y) ≈ f (x, y) +

∂f (x, y)

x +

∂f (x, y)

y .

(1.6)

∂y

∂x

Let u = f (x1 , x2 ,…, xm ) is a

function

of m variables. The

differential is

given by

du =

∂u

dx1 +

∂u

dx2

+ …+

∂u

dxm .

∂x

The chain rules. The theorem in Sec. 2.2 is the basis for the chain rules for differentiating composite functions of more than one variable. Theorem 1 of this section concerns the case in which z is a function of x and y, and x and y are functions of one variable. Theorem 2 concerns the case in which z is a function of x and y, and x and y are, in turn, functions of two variables.

Chain rule. Let z = f(x, y) have continuous partial

Theorem 1

derivatives z

′

and

z′

and let x = x(t) and y = y(t) be

differentiable functions of t. Then z is a differentiable function of t and

dz =

∂z dx

∂z

dy .

∂x dt

∂y dt

Chain rule. Let z = f(x, y) have continuous partial

Theorem 2

derivatives z′

and z

′ and let x = x(u, v) and y = h(u, v) be

differentiable functions of t and u. Then z is indirectly a

function of t and u, and

∂z

∂x

∂z

∂y

and

∂z

∂x +

∂z

∂y .

∂y ∂u

∂v

∂u

∂x ∂u

∂x ∂v

∂y ∂v

The differential

of z = f (x, y) ,

where

x = x(u, v) and y = y(u, v) can be

thought of as

dz =

∂f

dx +

∂f

dy ,

(1.7)

∂y

∂x

where dx =

∂x

du + dx dv , dy =

∂y

du +

dv .

∂u

∂v

∂u

∂v

http://vk.com/studentu_tk, http://studentu.tk/

2.4. Higher partials and differentials

If z = f(x, y), then not only is z a function of x and y, but also

z′

and z′

are

z′ and

each functions of x and y. Hence we may differentiate

z′

to obtain

second-order partial derivative of z. Symbolically,

′′

means

′ ′

′′

means

′ ′

zxx

(zx ) x ,

zxy

(zx ) y ,

′′

means

′ ′x

′′

means

′ ′ y

zyx

(zy )

zyy

(zy )

In terms of ∂ –– notation,

∂ 2 z

∂

∂z

∂ 2 z

∂

∂z

means

∂x2

∂x

∂x∂y

∂y

∂x

∂ 2 z

∂

∂z

∂ 2 z

∂

∂z

means

∂y∂x

∂x

∂y

They are also denoted

′′

∂ 2 f

and so on.

∂x 2

Note that to find

z′′

, and

∂ 2 z

first differentiate z with respect to x.

∂x∂y

For most functions met in practice the two “mixed partials” z′′

and

z′′

are

equal. In view of the importance of this remark it is stated as a theorem.

Mixed

partial. If z = f(x, y) has continuous partial

Theorem

derivatives

z′ ,

z′

, z′′

and

z′′

, then

z′′

= z′′ .

For a function

u = f (x1 , x2 ,…, xm )

exist

m2 second-order

partial

∂ 2u

∂

∂z

derivatives:

i, k = 1, 2, …, m .

∂xk ∂xi

∂xk

∂xi

We can extend our notation beyond second-order partial derivatives.

′′′

∂ 3 z

(or

∂x2∂y ) is a third-order partial derivative of z. It is the

For example, zxxy

′′

∂ 2 z

partial derivative of

(or ∂x2

zxx

Second-order differential d 2 z

of a function

z = f (x, y) at point

M (x, y) is

called the differential of the first-order differential dz , thus d 2 z = d (dz) .

http://vk.com/studentu_tk, http://studentu.tk/

<<< < Предыдущая 12 / 252 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.20252 Мб0Hidr_lab_Engl.DOC
#
19.02.20167 Мб208Higher Mathematics. Part 3.pdf
#
19.02.20167 Мб1118Higher_Mathematics_Part_1.pdf
#
19.02.20169 Мб100Higher_Mathematics_Part_1.pdf
#
19.02.20167 Мб417Higher_Mathematics_Part_2.pdf
#
19.02.201610 Мб48Higher_Mathematics_Part_2.pdf
#
19.02.20167 Мб128Higher_Mathematics_Part_2.pdf
#
19.02.20169 Мб308Higher_Mathematics_Part_3.pdf
#
19.02.2016695 Кб15HiraganaKatakanaWorkSheet (1).pdf
#
11.09.2019192 Кб1hjuj;f.docx
#
27.11.2019386 Кб10How Airplanes Work.doc