
Higher_Mathematics_Part_2
.pdf
5.7. Three trigonometric substitutions |
|
|||
Integrals in the form |
∫ R(x, |
ax 2 + bx + c )dx can be found by using a |
||
trigonometric substitution, if the integrand is a rational function of x and: |
||||
1. |
a − x2 |
let |
x = |
a sin t. |
2. |
a + x2 |
let |
x = |
a tg t. |
3. |
x2 − a let |
x = |
a sect. |
|
The motivation behind this general procedure is quite simple.
1. If you replace x in a − x2 by |
x = a sin t you obtain: |
a − x2 = a − ( a sin t)2 |
= a − a sin2 t = a 1− sin2 t = |
=  a
a  cos2 t =
cos2 t =  a cost.
a cost.
The important thing is that the square root sign disappears.
2. |
a + x2 = |
a + a tg2 t = |
a |
1+ |
sin2 t |
|
= |
|
|||
cos2 t |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
= |
a |
cos2 t + sin2 t |
= |
a |
= a sec t. |
||||
|
|
|
cos2 t |
cost |
|||||||
|
|
|
|
|
|
|
|
||||
3. |
x2 − a = |
a |
− a = |
a |
1− cos2 t |
= a tg t. |
|||||
|
|
cos2 t |
|
|
|
cos2 t |
|
|
|
|
|
|
Т.5 |
|
|
Typical problems |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Find the integrals |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1. ∫ |
|
|
|
dx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − x − 2x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Solution. Complete the square: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
2 |
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
1 |
|
2 |
|
1 |
|
|
1 |
|
|
|
|
9 |
|
|
|
1 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1−x − |
2x |
|
=−2 x |
|
+ |
|
|
− |
|
|
= −2 |
|
x + |
|
|
|
− |
|
|
|
− |
|
|
|
= |
2 |
|
− |
|
x + |
|
|
|
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
4 |
|
|
16 2 |
|
16 |
|
|
|
4 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Then |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
∫ |
|
|
|
dx |
|
= ∫ |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
= 1 |
|
∫ |
|
|
|
d(x + 1/ 4) |
2 |
= |
|
|
|
||||||||||||
|
|
1 − x − 2x2 |
|
|
|
|
|
|
9 |
− (x + |
1 |
) |
2 |
] |
|
2 |
|
|
|
3 |
2 |
|
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2[ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− x |
+ |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
16 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
arcsin x + 1/ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
= |
1 |
= |
|
|
1 |
|
arcsin 4x + 1 |
+ C . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 / 4 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
131 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
http://vk.com/studentu_tk, http://studentu.tk/
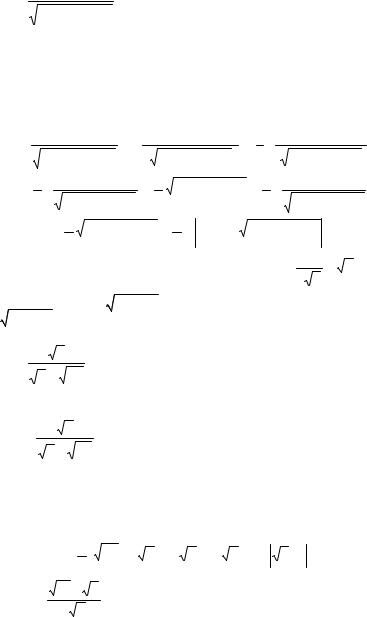
|
2. ∫ |
(x − 2)dx |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
4x |
2 + 4x + 17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
derivative (4x 2 + 4x + 17)′ = 8x + 4 , |
|
|
|
|
|
|
||||||||||||||||||||||
|
Solution. |
|
Given the |
|
the |
numerator |
|||||||||||||||||||||||||
transforms to the form: |
|
|
|
|
|
|
1 |
|
|
|
5 |
|
|
1 |
|
|
|
|
|
|
|
5 |
|
|
|||||||
|
x − 2 = |
1 |
(8x + 4) − |
4 |
− 2 = |
(8x +4)− |
= |
|
(4x2 +4x +17)′− |
. |
|
||||||||||||||||||||
|
|
8 |
|
|
8 |
|
|
|
|||||||||||||||||||||||
|
Then |
|
8 |
|
|
|
|
|
|
8 |
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(8x + 4) − |
5 |
)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∫ |
(x − 2)dx |
|
= ∫ ( |
|
|
|
1 |
|
∫ d(4x 2 + 4x + 17) − |
|
||||||||||||||||||||
|
|
8 |
2 |
= |
|
|
|||||||||||||||||||||||||
|
|
4x 2 + 4x + 17 |
|
|
|
|
4x 2 + 4x + 17 |
|
8 |
|
|
|
4x 2 + 4x + 17 |
|
|||||||||||||||||
|
− |
5 ∫ |
|
|
|
|
dx |
|
= |
1 |
|
4x 2 + 4x + 17 − 5 |
∫ |
d(2x + 1) |
= |
|
|
||||||||||||||
|
|
2 |
|
4x |
2 |
+ 4x + 17 |
4 |
|
|
|
|
|
|
4 |
|
(2x + 1) |
2 |
+ 16 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
= 1 |
|
4x 2 + 4x + 17 − |
5 ln 2x + 1+ 4x 2 |
+ 4x + 17 + C. |
|
|
|
|
||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
∫ 2 u |
|
|
|
|
|
|
||
|
We |
used |
|
the |
|
given |
|
|
table |
integrals: |
|
|
|
u |
+ C |
and |
|||||||||||||||
|
|
|
|
|
|
|
du = |
||||||||||||||||||||||||
|
du |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∫ |
|
= ln |
u + u2 ±a2 |
+C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
u2 ±a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3. ∫ |
3 |
x |
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x + 3 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Solution. The smallest multiple of 2 and 3 is 6. This suggests the substitution x = t 6 , dx = 6t 5 dt . Then
∫ |
3 x |
dx = ∫ |
|
|
t 2 |
|
|
|
|
5 |
|
|
|
6∫ |
t 4 |
|
|
6∫ |
(t 4 |
− 1) + 1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
6t |
|
dt = |
|
|
dt = |
|
|
|
|
|
dt |
= |
||||||||||||
|
|
|
t |
3 |
+ t |
4 |
|
t + |
|
|
t + 1 |
|||||||||||||||||||||
|
x + 3 x 2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||
|
6∫ |
|
(t 2 + 1)(t − 1)(t + 1) + 1 |
|
= 6∫(t 2 + 1)(t − |
|
|
6∫ |
|
|
dt |
|
|
|
|
|
||||||||||||||||
= |
|
|
|
|
|
|
|
|
dt |
1)dt + |
|
|
|
= |
|
|||||||||||||||||
|
|
t + 1 |
|
|
|
|
|
t + 1 |
|
|||||||||||||||||||||||
= 6∫ (t 3 − t 2 + t − 1)dt + 6∫ |
|
dt |
|
= |
|
3 |
t 4 |
− 2t 3 |
+ 3t 2 |
− 6t + 6 ln |
|
t + 1 |
|
+ C = |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
t + 1 |
2 |
|||||||||||||||||||||||||||||||
|
|
|
|
3 3 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
− 2 x + 3 3 |
x − 6 6 x + 6 ln 6 x + 1 + C . |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. I = ∫ |
x34− 3 x dx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
6 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
132 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
http://vk.com/studentu_tk, http://studentu.tk/

Solution. |
I = |
|
|
x = t12 ; |
|
|
|
|
|
|
|
|
= ∫ |
|
(t18 − t4 )12t11dt |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
dx = 12t11dt; |
|
|
|
|
|
|
6t3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
27 |
|
|
|
|
t |
13 |
|
|
|
|
||||
|
|
= 2 |
∫ |
(t18 |
|
− t4 )t8dt = 2 |
∫ |
(t26 |
− t |
12 )dt = 2 |
|
|
|
|
|
− |
|
|
+ C = |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
13 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
= 2x2 12 x3 |
− |
2x12 x |
+ C = |
|
2x2 4 x |
− |
2x12 x |
+ C. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|||||||||||
5. I = ∫ |
33 x − 1 + xdx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
3x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3x − 1 = t6 |
|
|
|
|
|
|
t3 + |
t6 |
+ |
|
1 |
2t5dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Solution. |
I = |
|
x = |
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
+ |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
3 |
|
3 |
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dx = 2t5dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
∫ |
(3t6 |
+ t9 + t3 )dt = |
|
2 |
|
|
3t |
7 |
|
|
|
|
|
|
t |
10 |
|
|
|
|
|
t |
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
+ |
|
|
+ |
|
|
+ C = |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
7 |
|
|
|
|
|
10 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
= |
2 |
(3x −1) 6 3x −1 + |
1 |
(3x −1) 3 |
|
(3x −1)2 |
+ |
1 |
3 (3x −1)2 + C. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
15 |
|
6 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. ∫ |
x 24+ 1+ x dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Solution. Let1+ x = t 4 , then |
|
|
x = t 4 − 1 , |
dx = 4t 3 dt . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Consequently, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∫ x 24+ 1+ x dx = ∫ |
(t 4 − 1)2 + t 2 |
4t 3dt = 4∫ ((t 4 − 1)2 + t 2 )t 2 dt = |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1+ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
4 |
|
|
|
|
8 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
||||||||||||||
|
= 4∫ (t |
10 |
|
|
2t |
6 |
|
+ t |
2 |
+ t |
4 |
)dt |
|
|
|
t |
11 |
|
t |
7 |
|
|
|
t |
3 |
|
|
|
t |
5 |
+ C = |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
= |
|
|
|
− |
|
|
|
+ |
|
|
|
+ |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
7 |
|
|
3 |
|
|
5 |
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
= 4 4 |
(1 |
+ x)11 |
|
− |
8 4 |
(1+ x) |
7 + |
|
|
4 4 (1+ x)3 + 4 4 |
(1+ x)5 + C . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
7. ∫ |
|
|
dx |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 (x −1)3 (x + 2)5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Solution. |
|
In |
this |
|
|
|
case |
|
|
4 (x − 1)3 (x + 2)5 |
|
|
|
= (x − 1)(x + 2) 4 |
x + 2 |
and an |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 1 |
|
integrand is a rational function of |
|
x and 4 |
x + 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
133 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
http://vk.com/studentu_tk, http://studentu.tk/
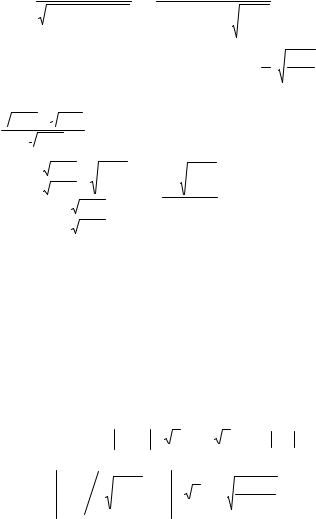
The substitution |
x + 2 |
= t 4 is appropriate: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
x − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x = |
t 4 |
|
+ 2 |
, |
|
|
x − 1 = |
|
3 |
|
|
, |
x + 2 = |
|
3t 4 |
|
|
dx = − |
|
12t 3dt |
|
. |
|
|
||||||||||||||||
|
|
|
|
|
t 4 |
− 1 |
|
|
|
|
|
|
|
t4 |
− 1 |
|
|
|
|
|
t 4 |
− 1 |
|
|
(t 4 |
− 1)2 |
|
|
|
|
||||||||||||
Then |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
= |
∫ |
|
|
|
|
|
|
dx |
|
|
|
|
|
= |
|
|
|
|
|
||||
|
|
|
|
|
4 (x −1)3 (x + 2)5 |
|
|
|
|
|
|
|
|
|
|
4 |
x + 2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
(x − 1)(x + 2) |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x − 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= ∫ |
t 4 |
− 1 |
|
t 4 |
|
− 1 |
|
1 |
|
− 12t 3 |
|
dt = |
− |
4 |
∫ |
dt |
= |
4 |
|
+ C = |
4 |
4 |
x − 1 |
+ C . |
||||||||||||||||||
|
3 |
|
3t |
4 |
|
t |
|
(t |
4 |
− 1) |
2 |
3 |
t |
2 |
|
|
3t |
|
3 |
x |
+ |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
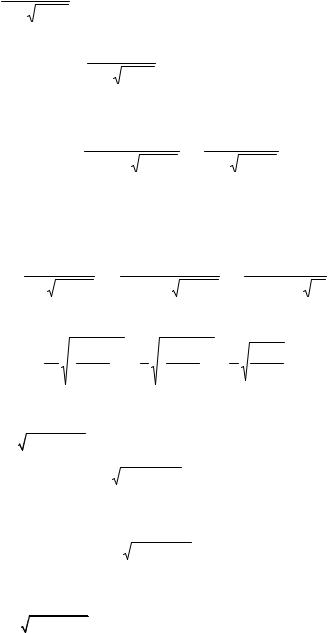
8.I = ∫  x − 2 −
x − 2 −  x + 1dx.
x + 1dx.
x x − 2
x − 2
|
|
|
|
|
|
|
|
|
|
x − 2 |
|
− |
|
x + 1 |
|
|
1 |
− |
|
x +1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x − 2 |
|
x − 2 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 2 |
|
|
|
|
|||||||||||||||
Solution. I = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = ∫ |
|
x |
dx = |
|
||||||||||||||
|
|
|
x |
|
|
|
x − |
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x + 1 |
= t2 |
x + 1 = xt2 − 2t2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
x − 2 |
|
|
|
|
|
(1− t) t (t2 −1)dt |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= |
xt |
2 |
− x |
= 2t |
2 |
+ 1 |
x = |
2t2 + 1 |
|
= −6∫ |
= |
|||||||||||||||||||||
|
|
|
|
t2 −1 |
|
(2t2 + 1)(t2 −1)2 |
|||||||||||||||||||||||||||
|
|
|
dx = − |
|
6tdt |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
(t2 −1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
= 6∫ |
|
|
|
|
|
(t −1) tdt |
|
= 6∫ |
|
|
tdt |
|
||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
||||||||||||||||||||||||
|
|
|
|
|
(2t2 + 1)(t −1)(t + 1) |
(2t2 + 1)(t + 1) |
|
||||||||||||||||||||||||||
|
∫ |
|
2t + 1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
= 2 |
|
|
|
|
− |
|
|
|
|
dt = |
|
ln 2t |
|
|
+ 1 + |
|
2 arctg( |
|
2t) − 2 ln t + 1 + C = |
||||||||||||||
2t2 + 1 |
t + 1 |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3x |
|
x + 1 |
|
= ln |
|
|||
|
|
|||
|
x − 2 |
|
x − 2 |
|
|
|
2 |
+ |
2arctg 2(x + 1) + C. |
+ 1 |
||
|
|
x − 2 |
|
|
134
http://vk.com/studentu_tk, http://studentu.tk/

Integration of the binomial differentials
9. ∫  x (3 − 3 x )2 dx .
x (3 − 3 x )2 dx .
Solution. Multiplying the integrand we get
1 1 2 1 5 7
∫  x (3 − 3 x )2 dx = ∫ x 2 (9 − 6x 3 + x 3 )dx = ∫ (9x 2 − 6x 6 + x 6 )dx =
x (3 − 3 x )2 dx = ∫ x 2 (9 − 6x 3 + x 3 )dx = ∫ (9x 2 − 6x 6 + x 6 )dx =
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
36 |
|
|
11 |
|
|
|
|
6 |
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 6x |
2 |
− |
|
x |
6 |
+ |
|
x |
6 |
|
|
+ C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
11 |
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
10. I = ∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
x (3 x + 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Solution. This p is an integer number and is equal to |
|
|
−2. Thus: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
I = ∫ x |
− |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
−2 |
|
|
|
|
|
|
|
|
|
|
x = t |
6 |
; |
|
|
|
= 6∫ |
|
|
|
t |
2 |
dt |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
+ |
1 dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
dt; |
|
(1+ t |
2 |
|
2 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = 6t |
|
|
|
|
|
|
|
) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
− |
|
|
3t |
|
|
|
+ 3arctgt + C = − 36 x |
|
+ 3arctg 6 |
x + C. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1+ t2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ 3 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
11. I = ∫ |
|
|
|
5 |
|
xdx |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
3 − 25 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Solution. Multiplying the integrand we get |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
xdx |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I = ∫ |
|
|
|
= |
∫ x5 (3 − 2x5 )2 dx. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 − 25 x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Here m = |
|
1 |
; n = |
3 |
|
and |
|
m + 1 |
= 2 |
|
– an integer number. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 − t2 |
5 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
− |
1 |
|
|
|
|
|
|
3 − |
2x5 = t |
|
|
x = |
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Thus I = |
x5 |
|
− 2 |
x |
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
= |
|||||||||||||||||||||||||
|
|
3 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
3 − t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = − |
|
|
t |
|
|
|
|
|
|
|
|
dt; |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
3 − t2 |
|
|
|
|
|
−1 5 |
|
|
3 |
− t2 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt = − |
|
|
|
∫(3 − t )dt = |
|||||||||||||||||||||||||||
|
|
|
|
= ∫ |
|
|
2 |
|
|
|
|
|
|
|
|
|
t |
2 |
|
|
|
|
6 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
= − |
5 |
t + |
|
5 |
|
t3 |
|
+ C = |
|
5 |
|
|
|
(3 − 25 x3 )3 − |
5 |
|
|
|
3 − 25 x3 + C. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
18 |
|
18 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
135 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
http://vk.com/studentu_tk, http://studentu.tk/





 x
x 
 Answers
Answers