
- •Основы системного анализа Раздел 1. Введение
- •Раздел 2. Имитационное моделирование как метод исследования систем большой сложности
- •Раздел 3. Основы теории систем массового обслуживания
- •Введение
- •1. Системность как всеобщее свойство матери
- •1.1. Определение системы
- •1.2.Сложная и большая система
- •1.3. Классификация систем по их основным свойствам
- •1.4. Искусственная система как средство достижения цели
- •1.5. Системность как всеобщее свойство материи
- •1.6. Системность познавательных процессов
- •1.7. Методология системного подхода
- •1.8. Развитие системных представлений в науке и практике
- •1.9. Контрольные вопросы и упражнения к разделу 1.1.
- •Раздел 2. Имитационное моделирование как метод исследования систем большой сложности
- •2.1. Введение
- •2.2. Основные понятия
- •2.3. Принципы и методы построения имитационных моделей
- •2.4. Вопросы для самопроверки
- •2.5. Упражнения
- •2.6. Случайные события и их имитация
- •2.7. Имитация случайного события
- •2.8. Имитация сложного события
- •2.9. Имитация сложного события, состоящего из зависимых событий
- •2.10. Имитация событий, составляющих полную группу
- •2.11. Вопросы для самопроверки
- •2.12. Упражнения
- •2.13. Имитация непрерывных случайных величин
- •2.14. Метод обратной функции
- •2.15. Метод Неймана (режекции)
- •2.5, Где
- •2.16. Алгоритм получения значения нормально распределенной случайной величины
- •2.17. Алгоритм получения случайной величины, распределенной по Пуассону
- •2.18. Упражнения
- •2.19. Алгоритмы получения значений систем случайных величин (случайных векторов)
- •2.20. Метод аналитических преобразований
- •2.21. Метод разложения по координатным случайным величинам
- •2.22. Алгоритм получения значений системы дискретных случайных величин
- •2.23. Упражнения
- •2.24. Имитация случайных процессов
- •2.25. Имитация нестационарных случайных процессов
- •2.26. Имитация стационарных сп
- •2.27. Имитация стационарных нормальных сп
- •2.28. Обработка результатов моделирования
- •Раздел 3. Основы теории систем массового обслуживания
- •3.1. Введение
- •3.1.1. Историческая справка
- •3.1.2. Примеры систем массового обслуживания. Анализ задач тсмо
- •3.1.3. Понятия, определения, терминология
- •3.1.4. Классификация смо
- •3.1.5.Основная задача тсмо
- •3.2. Математические модели потоков событий
- •3.2.1. Регулярный и случайный потоки
- •3.2.2. Простейший пуассоновский поток
- •3.2.3. Свойства простейшего пуассоновского потока
- •3.2.4. Простейший поток и решение практических задач
- •3.2.5. Нестационарные пуассоновские потоки
- •3.2.6. Потоки с ограниченным последствием (потоки Пальма)
- •3.2.7. Потоки восстановления
- •Термины и определения
- •Литература
2.13. Имитация непрерывных случайных величин
Имитационное моделирование явлений и объектов, формальное описание которых возможно с помощью представления их в виде случайных величин (СВ) с заданным законом распределения, основываются на использовании СЧ с равномерным законом распределения и их преобразований. Такие преобразования могут быть осуществлены на основе: метода обратной функции; предельных теорем теории вероятности, приближенных методов и т.п. Для более подробного ознакомления с этими методами можно воспользоваться [20, 25].
2.14. Метод обратной функции
Пусть непрерывная случайная величина
(СВН)
![]() задана своим законом распределения:
задана своим законом распределения:

где
![]() –
плотность распределения вероятностей,
а
–
плотность распределения вероятностей,
а![]() -
функция распределения вероятностей.
Доказано, что случайная величина
-
функция распределения вероятностей.
Доказано, что случайная величина

распределена равномерно на интервале (0,1).
Отсюда следует, что искомое значение
![]() может быть определено из уравнения:
может быть определено из уравнения:
 (5)
(5)
которое эквивалентно уравнению:
![]()
где y – значение случайной величины![]() .Решение уравнения (6) можно записать в
общем виде через обратную функцию
.Решение уравнения (6) можно записать в
общем виде через обратную функцию![]()
![]()
Основной недостаток метода заключается в том, что интеграл (5) не всегда является берущимся, а уравнение (6) не всегда решается аналитическими методами.
Пример 1.
Получить в соответствии с методом
обратной функции преобразование,
позволяющее вычислить значения СВ![]() ,распределенной по показательному
закону.
,распределенной по показательному
закону.
Решение. Показательный закон характеризуется функцией плотности:
![]()
Воспользуемся методом обратной функции, вычислим интеграл (5) и получим уравнение вида (6)
 или
или![]() Тогда:
Тогда:![]() ,
прологарифмировав и разрешив уравнение
через y, будем иметь:
,
прологарифмировав и разрешив уравнение
через y, будем иметь:
![]() (7)
(7)
Получая значение х с помощью датчика равномерно распределеных случайных чисел на интервале (0,1), можно получить значения yв соответствии с выражением (7). Заметим, что показательный закон распределения особенно часто используется для исследования систем массового обслуживания и определения показателей надежности систем.
Пример 2.
Получить преобразование в соответствии
с методом обратной функции СВ![]() ,
позволяющее вычислить значение СВ
,
позволяющее вычислить значение СВ![]() , распределенной по закону Вейбулла.
, распределенной по закону Вейбулла.
Решение. Плотность распределения такой СВ имеет вид:
![]()
![]() -
параметры закона распределения, введем
обозначение
-
параметры закона распределения, введем
обозначение![]() .
Нетрудно вывести уравнение вида (6). Для
данного распределения оно имеет вид:
.
Нетрудно вывести уравнение вида (6). Для
данного распределения оно имеет вид:
![]()
Логарифмируя левую и правую его части и выражая yчерезх, получим:
![]()
Распределение Вейбулла имеет место при
исследовании отказов элементов
оборудования, возникающих в результате
износа и старения. Параметр![]() носит название и имеет смысл интенсивности
отказов. При a =1 закон Вейбулла совпадает
с показательным, при a <1 интенсивность
отказов является монотонно убывающей,
а при a >1 – монотонно возрастающей
функцией.
носит название и имеет смысл интенсивности
отказов. При a =1 закон Вейбулла совпадает
с показательным, при a <1 интенсивность
отказов является монотонно убывающей,
а при a >1 – монотонно возрастающей
функцией.
2.15. Метод Неймана (режекции)
Метод Неймана, так же как метод обратной функции, является методом, позволяющим получить значения СВ в соответствии с заданным законом распределения. Этот метод является достаточно универсальным он применим для моделирования всех СВ, значения которых не выходят за пределы ограниченного интервала (a,b), а также для СВ, законы распределения которых можно аппроксимировать усеченными.
Метод Неймана состоит в следующем:
С помощью датчика случайных чисел получают пару чисел, распределенных равномерно на (0,1).x1 и x2.
Путем преобразований (по методу обратной функции получают два числа
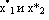 ,
равномерно распределенных соответственно
на интервалах (a,b) и (o,w), то есть
,
равномерно распределенных соответственно
на интервалах (a,b) и (o,w), то есть
