2.6. Случайные события и их имитация

Б. Циглер в своей книге “Теория моделирования и имитации”, сравнивает роли арифметики и имитационного моделирования. Он пишет: “Никто не знает вопросов о роли арифметики в науке, инженерной деятельности или управлении. Арифметика применяется повсюду, однако она – математическая дисциплина, имеющая свои собственные аксиомы и свою логическую структуру… Ее содержание применимо ко всем дисциплинам. Практика моделирования и имитации также используется повсюду. Аналогично арифметике, она имеет собственные понятия: “модельное описание”, “упрощение”, … “имитация”, “квантование” и т.д.”. Изложению ее, специфических понятий, приемов и методов имитационного моделирования посвящены параграфы 2-5 данного раздела. Материал этих параграфов имеет справочный характер, ориентирован на описание алгоритмов и их практическое применение и не содержит доказательств, которые можно найти, например, в [1,4].

2.7. Имитация случайного события

Пусть некоторое событие А происходит с вероятностью . Требуется воспроизвести факт наступления события А. Поставим в соответствие событию А событие В, состоящее в том, что х меньше либо равно, где х здесь и в дальнейшем – случайное число (СЧ) с равномерным на интервале (0,1) законом распределения. Вычислим вероятность события В:

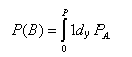
Таким образом, события А и В являются равновероятными. Отсюда следует процедура имитации факта появления события А. Она сводится к проверке неравенства х_{Аменьше, либо равно}Р, а алгоритм заключается в следующем:

1. С помощью датчика случайных чисел (СЧ) получают СЧ х;

2. Проверяют выполнение неравенства х меньше, либо равно ;

3. Если оно выпоняется, то событие А – произошло, если нет – то произошло

2.8. Имитация сложного события

Имитация сложного события, состоящего, например, из двух независимых элементарных событий А и В, заключается в проверке неравенств:

,

где и– вероятности событий А и В, а х₁ и х₂– СЧ с равномерным законом распределения.

В зависимости от исхода проверки неравенств (аналогично алгоритму 2.1.) делается вывод какой из вариантов:

имеет место.

2.9. Имитация сложного события, состоящего из зависимых событий

В случае, когда сложное событие состоит из элементарных зависимых событий А и В имитация сложного события производится с помощью проверки следующих неравенств:

В зависимости от того, какая из этих четырех систем неравенств выполняется, делается вывод о том, какой из этих четырех возможных исходов имеет место.

В качестве исходных данных задаются _,и условная вероятность, вероятность может быть вычислена. По формуле полной вероятности:

2.10. Имитация событий, составляющих полную группу

Пусть событие А_i(i=1,n) составляют полную группу, тогда их вероятности Р_i, таковы что:

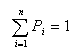
Имитация факта появления одного из событий А_i(i=1,n) сводится к проверке следующих неравенств:

Выполнение К-го неравенства эквивалентно выполнению события А_К. Описанный алгоритм называют иногда алгоритмом “розыгрыша по жребию”. Его можно интерпретировать как установление номера К-го отрезка длинной Р_К, на который пало СЧ х, при условии разбиения отрезка единичной длины на отрезки с длинами P1,P2,...Pn (рис 3.3.)

Рис. 3.3.

2.11. Вопросы для самопроверки

1. Как Вы понимаете смысл слов “имитация факта наступления события” и “имитация события”? В данном тексте это одно и тоже?

2. Докажите, что алгоритмы имитации сложных событий (параграфы 2.8. и 2.9.) могут быть сведены к имитации полной группы событий, сравните их. Какие алгоритмы предпочтительнее?

3. Докажите справедливость алгоритмов, описанных в параграфе 2.8.