23. Неявные функции.

Опр 1. Отображение Fназывается непрерывно дифференцируемым на множестве X,если все его коорди­натные функции непрерывно дифференцируемы на X,т.е. все его частные производные непрерывны на X.

Теорема 12. Пусть выполняются условия:

1) Отображение F(x,y) непрерывно дифференцируемо в некоторой окрестности точки (a,b)€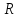^n+m

2)F(a,b)= 0.

3)detF"_y(a,b)≠0.

Тогда существуют окрестности V(a)€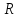ⁿU(b)€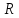^т, что для любогоx€ V(a) существует и притом единственное значение y€U(b), что F(x,y)= 0. Если y= f(x) указанное решение, то отображение f непрерывно дифференцируемо на множестве V(a), причем b= f(a).

24. Обратное отображение.

Теорема 13. Пусть f : X →Rⁿ, X СRⁿ, причем:

1. отображение f непрерывно дифференцируемо в некоторой окрестности точки a € X;

2. f (a)= b;

3. det f'(a)≠0.

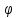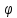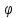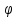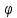Тогда существуют окрестности V(a) С Rⁿ, U(b) С Rⁿ и существует обратное отображение =f^-1такое, что :U(b)→V(a), - единственно, (b) = a и отображение непрерывно дифференцируемо наU(b).

Доказательство. Рассмотрим функцию F(x,y)=f(x)—y.Тогда отображение y=f(x)запишется в виде F(x,y)=0.Из условий теоремы 12 следует, что F(x,y)непрерывно дифференцируема в некоторой окрестности точки (a,b)и F(a,b)=0,detF_x^'( a, b) = detf^'(a)≠0.Таким образом, выполняются все условия теоремы о неявной функции, откуда и следует утверждение данной теоремы.

25. Необходимые условия зависимости функций.

Пусть на открытом множестве G€Rⁿ задано mнепрерывно дифференцируемых функцийy_i=f_i(x),x € G, i = 1,m.(1)

Если существует открытое множество D С R^m-1и непрерывно дифференцируемая на Dфункция F :D→R такая,что F(f₁(x),...,f_m-1(x))=fm(x),x € G, (2) то будем говорить, что функция f_mзависит от функций f₁(x),...,f_m-1 (x)на множестве G. Если среди функций (1) есть функция, зависимая от остальных на множестве G, то система функций (1) называется зависимой на множестве G. Если ни одна из функций (1) не зависит от остальных на множестве G, то система функций (1) называется независимой на множестве G. В вопросах зависимости функций (1) важную роль играет матрица Якоби. 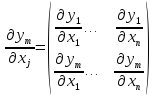(3)

Теорема 14.Пусть m<= n и система функций (1) является зависимой на открытом множестве G, тогда ранг матрицы Якоби меньше m в любой точке множества G.

Доказательство. Не нарушая общности рассуждений, будем считать, что f_mзависит от функций f₁, . . . , f_m-1на G, т.е. имеет место (2). Тогда из (2)

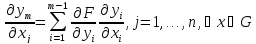
Отсюда следует, что m-ая строка матрицы (3) является линейной комбинацией остальных строк, следовательно ранг матрицы (3) меньше m, что и требовалось доказать. □

Следствие 1. Если m = n и система функций (1) зависимая на открытом множестве G, то

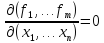
в каждой точке множества G.

Следствие 2 (достаточное условие независимости функций). Если m≤n ив какой-либо одной точке открытого множества G ранг матрицы (3) равен m, то система функций (1) является независимой на множестве G.

Доказательство. Пусть система функций (1) зависима на G, тогда в любой точке этого множества ранг меньше m. Пришли к противоречию. □

Поскольку элементы строк матрицы (3) являются координатами векторов gradfi(x),i = 1,…m, то теорему 14 можно сформулировать следующим образом:

Если m<=n и система функций (1) является зависимой на открытом множестве G, то векторы gradfi(x),i = 1,m линейно зависимы в каждой точке множества G.