50. Интеграл Дирихле.

Пусть ф-ция 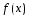абсолютно интегрируема на отр-ке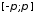. Подставив в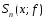выражения для коэффициентов Фурье получим:

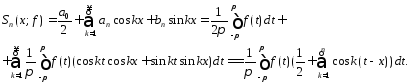Положим 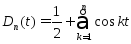, тогда: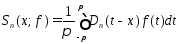

Ф-ция 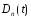наз. ядром Дирихле, а интеграл, стоящий в правой части этого рав-ва – интегралом Дирихле.

Лемма: Ядро Дирихле:

1. Четная, непрерывная, 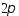- периодическая ф-ция, причём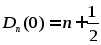

2. удовлетворяет условию

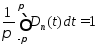
3. при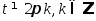имеет место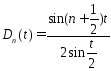

51. Сходимость рядов Фурье в точке(лемма 1)

Опр.: Функция 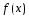непрерывна в точкеx справа(слева), если

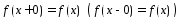
Опр.: Непрерывная справа(слева) функция 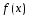имеет в точке х правую(левую) производную, если существует конечный предел

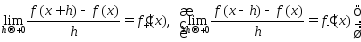
Если ф-ция непрерывна как справа, так и слева и 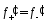в точке х, то функция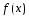имеет в точке х конечную производную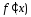, причем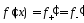

Опр.: Точка 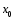называется регулярной точкой функци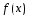и, если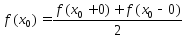

Составим вспомогательную ф-цию 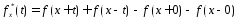. Если ф-ция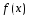регулярна в точке х, то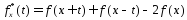

Лемма: Пусть -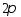периодическая, абсолютно интегрируемая ф-ция на отрезке длины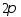. Тогда интегралы

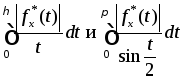, где 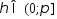сходятся и расходятся одновременно.

Доказательство: В силу аддитивности

Интеграл 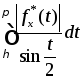является сходящимся, т.к. ф-цияявл. абсолютно интегрируемой ф-цией как сумма абсолютно интегрируемых функций, а функция 1/(sin(t/2)) является непрерывной на отрезке [].

Поскольку 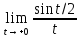=1/2, то на основе предельного признака сравнения несобственных интегралов заключаем, что интегралы 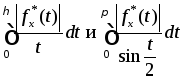сходятся и расходятся одновременно, так как функция fx *(t) абсолютно интегрируема, значит имеет только конечное число особых точек. Последнее позволяет выбрать ῆ так, что у функции

fx *(t)/t и fx *(t)/sin t/2 есть одна особенность t=0ю Полученное доказывает лемму

52. Признак Дини и следствия из него

Теорема4: Пусть выполняются условия:

1. Ф-ция 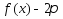-периодическая;

2. Ф-ция 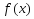абсолютно интегрируема на отрезке длины

3. x – точка непрерывности или точка разрыва 1-го рода на отрезке длины ;

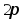4. интеграл 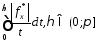абсолютно сходится.

Тогда ряд Фурье функции 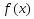сходится в точке х к значению.

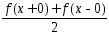Следствие 1. Если условия теоремы 4 выполнены, то в любой регулярной точке функции f (вчастности, во всех ее точках непрерывности) ряд Фурье этой функции сходится к ее значению в рассматриваемой точке. Следствие 1 непосредственно следует из теоремы в силу определения регулярной точки функции.

Следствие 2. Если f — 2п-периодическая функция, абсолютно интегрируемая на отрезке длины 2п, и в точке x существуют f(x+0), f (x—0), f+ ¹(x) и f— ¹(x), то ряд Фурье функции f сходится в этой точке к значению

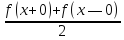
Следствие 3. Ряд Фурье кусочно дифференцируемой на отрезке [—п;п] функции f сходится в каждой точке интер-

вала (—п, п) к значе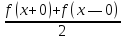ниюа в точкаx= —п и x= п к значению .

53. Суммирование рядов Фурье методом средних арифметических.

Пусть функция fабсолютно интегрируема на отрезке [ -п;п , ] и удовлетворяет условию f( -п ) = f(п ) , а следовательно, 2п-периодически продолжаема на всю действительную ось. Пусть S_n(x) -ее суммы Фурье, а D_n(x) - ядра Дирихле, n= 0,1, 2,...

Рассмотрим средние арифметические:

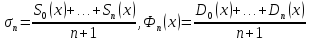
Сумма 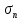называется суммой Фейераn-го порядка функции f, а Ф_n(x) — ядром Фейера n-го порядка.

Из формулы S_n(x) = 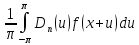получаем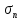=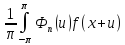du.

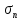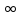Будем исследовать поведение сумм приn→,т.е. рассмотрим суммирование ряда Фурье методом средних арифметических.

Лемма 1. Ядра Фейера имеют следующие свойства:

1) Они являются непрерывными, четными, 2п-периодическим функциями и Ф_n(0)= ;

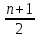2)

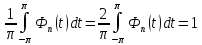
3) При t≠ 2пm, m€Z справедлива формула

Ф_n(t) =

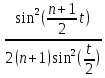
Доказ-во:Свойство 1) следует из соотв.свойств ядер Дирихле, например:

.

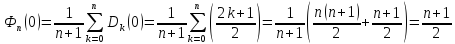Свойство 2) также следует из соответв. Свой-ва ядра Дирихле. .

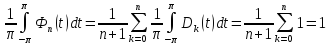Второе рав-во свойства 2) сразу следует из четности ядер Фейера. Докажем сво-во 3). Пусть t≠2пm, m€Z, тогда

.
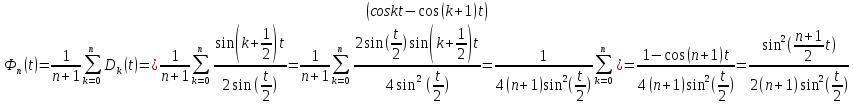