9. Последовательности точек пространства .

Определение 1. Последовательностью точек пространства Rⁿ называется функция f : N → Rⁿ , которая каждому натуральному числу k ставит в соответствие точку x^(k) =(x₁^(к), . . . , x_n)ϵ Rn .

Теорема1. Последовательность =()Rⁿ, к=1,2,… сходится к точке а=(а₁,…, а_n)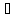Rⁿ тогда, и только тогда, когда 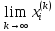=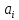, i=1,n.(2)

Доказательство : Согласно |x_i— y_i|≤p(x,y)≤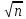max_1≤k≤n|x_k— y_k|, i = 1,…,n можем записать

|x_i^(k)-a_i| ≤p(x^(k),a) ≤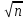max_1≤k≤n|x^(k)_j— a_j|, i=1,n (1)

Необходимость. Если 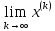=a, то для любого ε>0, ᴲNϵN→ p(x^(k),a)<ε,

а значит, согласно (1) выполняются неравенства |x_i^(k)-a_i|<ε, i=1,n. Откуда следует справедливость(2)

Достаточность Если имеет место (2), то для

Аε<0, E NϵN : A k>N→|x_i^(k)-a_i|<ε/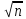, i=1,n

и, следовательно, max_1≤k≤n|x^(k)_j— a_j|<ε/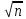

Тогда в силу (1) p(x(k),a) <ε, а это означает, =a.

Теорема 2. Из любой ограниченной последовательности {x^(k)} точек пространства Rⁿ можно выделить сходящуюся подпоследовательность.

10. Предел отображения.

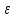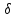Определение 1. Точка b€R^mназывается пределом отображения fв точке a, если для любого > 0 существует > 0 такое, что для любого x€X и 0 <p_n(x,a)<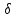следует, что p_m (f(x),b)<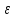.При этом пишут lim f(x) = b.(x→a).

Определение 2.Точка bϵR^mназывается пределом отображения fв точке a, если для любой окрестности U(b) существует V(a)такая, что если x€V(a)∩X, то f(x)€U(b).

Определение 3.Точка bϵR^mназывается пределом отображения fв точке a, если для любой последовательности x^(k)€X\{a},k = 1, 2,...сходящейся к точке a, последовательность {f (x^(k))}сходится к точке b.

Теорема 3. Точка b = (b₁,...,b_m) является пределом отображения f : X — R^m, X €Rⁿпри x→a тогда и только тогда, когда lim f_i(x)=b_i, i=1,m.(x—>a)

Доказательство. Справедливость теоремы непосредственно следует

|f_i(x)-b_i| ≤p(f(x), b) ≤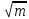max_1≤k≤m |f(x)_j— b_j|, i=1,m

и определения предела отображения.

Теорема 4.Отображение f : X →R^m, XСRⁿимеет предел в точке a тогда и только тогда, когда

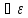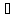>0V(a) : 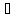х', x" €V(a)→ p_m(f(x¹), f (x"))<.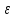

Теорема 5. Если отображение f :X — R^m, где X€Rⁿимеет предел в точке a, то:

1. предел единственный;

2. отображение fограниченно в некоторой проколотой окрестности V(a) точки aв множестве X.

Теорема 6.Пусть f : X →R^m, g : X →R^m, где X€Rⁿ, и существуют пределы limf (x) = b(x→a), limg(x) = c(x→a). Тогдасуществуют пределы:

1) lim (f (x) ± g(x))= b ± c;(x→a)

2) lim f(x) . g(x) = b . c,(x→a)

где f± g, b± c— есть сумма и разность векторов; f • g, b • c— скалярное произведение векторов.

Теорема 7. Пусть f:X— R, g:X— R, X€Rⁿ, и существуют пределы limf(x) = A(x→a), limg(x) = B.(x→a)Тогдасуществуют пределы:

1) lim(f(x) ± g(x))= A ± B,

x— a

2) limf(x)g(x) = A • B,

x— a

3) если g(x) ≠0,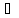x€V(a) иB≠0, то .

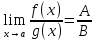Замечание 1 . Заметим, что вначале мы говорим, что существуют пределы отображений fи g, а только после этого можем говорить о существовании предела f ± gи f • g.

Замечание 2. Для пределов функций многих переменных справедливы и другие свойства аналогичные свойствам функ­ций одной переменной, при этом формулировки теорем и их доказательства по существу остаются теме же самыми.