
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
20.Формула Тейлора для функций многих переменных.
Теорема
9. Пусть функция f:
V(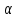 ,
,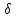 )→R,
V(
)→R,
V(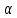 ,
,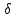 )
) Rn
определена и непрерывна вместе со всеми
частными производными до порядка m+1
включительно в
Rn
определена и непрерывна вместе со всеми
частными производными до порядка m+1
включительно в
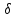 -окрестности
точки а, и х=a+h
ϵ V(
-окрестности
точки а, и х=a+h
ϵ V(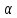 ,
,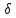 ).
Тогда справедлива формула
).
Тогда справедлива формула
f(x)=f(a)+ (h1
(h1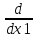 +…+
hn
+…+
hn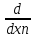 )kf(a)+rm(a,h),
(1)
)kf(a)+rm(a,h),
(1)
где
rm(a,h)=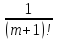 (h1
(h1 +…+
hn
+…+
hn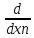 )m+1f(a
)m+1f(a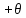 h),
0<
h),
0<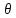 <1.(2)
<1.(2)
Доказательство.
Рассмотрим
функцию
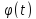 =
f(a+ht),
=
f(a+ht),
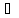 tϵ[0;1].
Эта функция, согласно условию, имеет
непрерывные производные до порядка m+1
включительно. По формуле Тейлора для
функции одной переменной имеем
tϵ[0;1].
Эта функция, согласно условию, имеет
непрерывные производные до порядка m+1
включительно. По формуле Тейлора для
функции одной переменной имеем
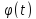 =
=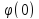 +
+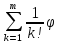 (k)(0)tk+rm(t),
(k)(0)tk+rm(t),
gde
rm(t)=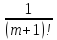
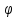 (m+1)(
(m+1)(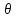 )tm+1,
)tm+1,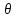 ϵ(0;1).Поскольку
ϵ(0;1).Поскольку
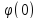 =f(a),
=f(a),
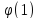 =f(a+h),
и
=f(a+h),
и
 =
=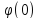 +
+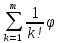 (к)(0)
+rm(1),
(3)
(к)(0)
+rm(1),
(3)
где
rm=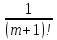
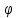 (m+1)(
(m+1)(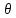 ),
),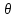 ϵ(0;1),
то из (3)
и
ϵ(0;1),
то из (3)
и
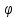 (к)(t)=
(h1
(к)(t)=
(h1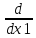 +…+
hn
+…+
hn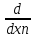 )kf(x
)kf(x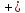 ht)
следует (1)
с остаточным членом, определенным
формулой (2).
ht)
следует (1)
с остаточным членом, определенным
формулой (2).
21. Необходимые условия экстремума.
Определение 1. Пусть функция f(x)определена на множестве XСRn. Точка a€ Xназывается точкой локального максимума (минимума) функции f, если существует окрестность V(a)такая, что для всех x€ V(a)выполняется неравенство f(x)≤f(a) (f(x)≥ f(a)).
Если для x€V(a)имеет место неравенство f(x)<f(a) (f(x)>f(a)), то точка a называется точкой строгого локального максимума (минимума) функции f.
Определение 2. Точки локального максимума и минимума функции fназываются точками локального экстремума функции f,а значения функции в этих точках называются локальными экстремума функции.
Теорема
10. Пусть
функция f
определена в окрестности V(a)С
Rnточки
a,
имеет в точке a
частные производные по каждой из
переменных x1,
. . . , xn.
Тогда для того, чтобы функция f
имела в точке a
локальный экстремум, необходимо, чтобы
в этой точке были выполнены равенства
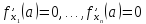 .(1)
.(1)
Док-во:
Рассм. ф-цию
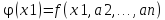 одной
переменной, опред., в силу условий
теоремы, в некоторой окрестности точки
a1
вещественной оси. В точке a1
ф-ция φ(x1)
имеет локальный экстремум, и поскольку
одной
переменной, опред., в силу условий
теоремы, в некоторой окрестности точки
a1
вещественной оси. В точке a1
ф-ция φ(x1)
имеет локальный экстремум, и поскольку
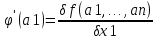 ,
то
,
то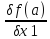 =0.
Аналогично док-тся и остальные равенства
системы(1).
=0.
Аналогично док-тся и остальные равенства
системы(1).
Точки, в которых выполнены условия (1), называются стационарными точками функции f.
Следовательно, если функция fимеет в точке aлокальный экстремум, то точка aявляется стационарной точкой функции fили функция fв этой точке не дифференцируема.
22. Достаточные условия локального экстремума.
Пусть функция f : V(a)→R имеет все непрерывные частные производные до второго порядка включительно в окрестности V(a)ʗRn точки а, а – стационарная точка функ. f.
Если
квадратичная форма
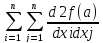 hihj
(1)
hihj
(1)
1) положительно (отрицательно) определена, то а явл.точкой строго лок.мин(макс) функции f;
2) неопределенна, то в точке а функция не имеет лок.экстр.
Док-во. Пусть h≠0, a+hϵV(a). Поскольку а стц.точка функции, то разложение f по формуле Тейлора при m=2
f(a+h)-f(a)=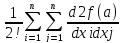 hihj+o(
hihj+o(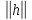 2)=
2)=
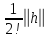 2(
2(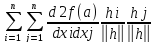 +o(1))(2)
+o(1))(2)
где
o(1)
– бесконечно малая при h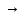 0
0
Из (2) видно, что знак разности f(a+h)-f(a) полностью определяется знаком величины, стоящей в правой части.
Вектор
е=(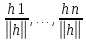 )
имеет единичную норму. Квадр.форма (1)
непрер.как функцияh
в Rn,
поэтому ее ограничение на единичную
сферу S(0;1)={xϵRn
|
)
имеет единичную норму. Квадр.форма (1)
непрер.как функцияh
в Rn,
поэтому ее ограничение на единичную
сферу S(0;1)={xϵRn
|
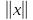 =1}
также непрерывно наS(0;1).
Но сфера S
есть замкнутое огран.подмножество в
Rn,
т.е. компакт. Следовательно, форма (1)
имеет на S
как тчоку минимума, так и точку максимума,
в которых она принимает соответственно
значения m
и M.
=1}
также непрерывно наS(0;1).
Но сфера S
есть замкнутое огран.подмножество в
Rn,
т.е. компакт. Следовательно, форма (1)
имеет на S
как тчоку минимума, так и точку максимума,
в которых она принимает соответственно
значения m
и M.
Если форма (1)
пол.опр., то 0<m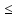 M
и, поэтому найдется число
M
и, поэтому найдется число
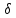 >0
такое, что при
>0
такое, что при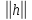 <
< будет
будет <m.
Тогда при
<m.
Тогда при
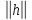 <
<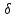 выражение в правой части равенства
(2)окажется положительным иf(a+h)-f(a)
>0 при 0<
выражение в правой части равенства
(2)окажется положительным иf(a+h)-f(a)
>0 при 0<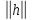 <
<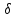 .
Т.о. точка а – точка строгого лок.мин.
рассматриваемой функции.
Аналогично
проверяется, что в случае отр.опр формы
(1) функция имеет в а строгий локальный
максимум.
.
Т.о. точка а – точка строгого лок.мин.
рассматриваемой функции.
Аналогично
проверяется, что в случае отр.опр формы
(1) функция имеет в а строгий локальный
максимум.
Если квадратичная форма (1) на единичной сфере или, что равносильно, в Rn принимает значения разных знаков. То в любой окрестности точки а найдутся как точки, в которых значение функции больше f(a), так и точки, в которых она меньше f(a). Следовательно, в этом случае а не явл.точкой локального экстремума рассматриваемой функции.
