14. Линейные отображения.

Определение 1. Отображение f :Rⁿ— R^mназывается линейным, если для любых двух векторов х', х'' € Rⁿ и любых двух чисел λ, μ € R выполняется равенство

f(λ х' +μ х") =λf(х') + μ,f(x").

Пусть {e₁,...,e_n}и {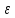₁,...,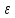_m}— фиксированные базисы пространств Rⁿ и R^m соответственно. При отображении fобраз вектора e_j,j=1,пявляется вектором в пространстве R^m и раскладывается по координатным векторам 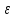_i, i = 1,m:

В силу линейности отображения fможно найти разложение по фиксированному базису {e_i,...,e_m}образ f(x) любого вектора x = x_ie_i+ - - - + x_ne_n€Rⁿ. А именно

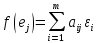
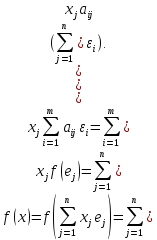
или в координатной записи f(x)=(fi(x),...,fm(x)),

где fi(x)=a₁₁x₁+…+a_1nX_n, … , fm(x)=a_m1x₁+…+a_mnX_n

Таким образом, отображение f :Rⁿ — R^mможно рассматривать как набор f = (f₁,...,f_m) из mкоординатных функций f₁: Rⁿ — R, i = 1,m.И заключаем, что отображение fл инейно тогда и только тогда, когда каждая координатная функция f_i : Rⁿ — R, i = 1,mлинейна.

15. Дифференцируемые отображения.

Дифференцируемость отображения в точке.

Определение 2.Отображение f:X →R^m, X СRⁿ, определенное на множестве X, называется дифференцируемым в точке x € X, предельной для множества X, если f(x+ h)—f(x)= L(x)h+ α(x;h), (1)

где L(x):Rⁿ→R^m— линейное относительно h отображение, а α(x;h)= o(h)при h—0, x+ h€X.

Теорема 1. Отображение f : X — R^m, X€Rⁿдифференцируемо в точке x € X, предельной для множества X, тогда и только тогда, когда в этой точке дифференцируемы функции f_i :X →R, i = 1,m, задающие координатное представление данного отображения.

Док-во. Если векторы f(x+h), f(x), L(x)h, α(a;h) из R^m записать в координатах, то равенство (1) окажется равносильным m равенствам

f_i(x+ h)—f_i(x)= L_i(x)h+ α_i(x;h), i=1,m

между действительными функциями, в которых L_i(x): Rⁿ→R – линейные функции, а α_i(x;h)=о(h) при h→0, x+hϵX, i=1,m

a_i(x) = 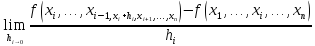(1.6)

Определение 3.Предел (1.6) называется частной производной функции f(x)в точке x=(x₁,...,X_n)по переменной x_i. Его обозначают одним из следующих символов

Утверждение 1. Если функция f:X→R, X СRⁿдифференцируема во внутренней точке x €X этого множества, то в этой точке функция имеет частные производные по каждой переменной и дифференциал функции однозначно определяется этими частными производными в виде

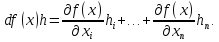
16.Свойства дифференцируемых отображений.

Теорема 2.Если отображения f : X →R^m, g : X →R^m, X С Rⁿдифференцируемы в точке x € X, то их линейная комбинация (λf+μg) : X →R^m также является дифференцируемым в этой точке отображением, причем имеет место равенство

(λf+μg)'(x)=(λf' + μg')(x).

Доказательство.(λf+μg)(x+h)—(λf+μg)(x)=(λf(x+h)+μg(x + h)) — (λf(x) + μg(x)) = λ(f(x+h)—f(x))+ μ(g(x + h)—g(x))=λ(f'(x)h + o(h)) + μ(g'(x)h + o(h) = (λf'(x)+μg'(x))h+o(h).□

Теорема 3. Если функции f:X→R, g:X→R, X С Rⁿдифференцируемы в точке x € X, то:1)их произведение дифференцируемо в точке x, причем (fg)'(x)= f'(x)g(x)+ f(x)g'(x); 2) их частное дифференцируемо в точке x, если g(x)≠ 0, причем

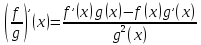
Доказательство теоремы аналогично случаю функции одной переменной. Теорема 4. Если отображение f:X →Y, X С Rⁿ, Y С R^m дифференцируемо в точке x € X, а отображение g:Y→R^s дифференцируемо в точке y= f(x), то их композиция 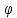= g о f:X →R^s дифференцируема в точке x и имеет место равенство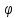'(x)= g'(y)f'(x).