
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
46.Почленное дифференцирование и интегрирование степенных рядов.
Теорема: Радиусы сходимости степенных рядов
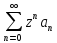 (1),
(1),
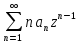 (2),
(2),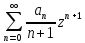 (3)
равны.
(3)
равны.
Доказательство:
Пусть R1,
R2,
R3–радиусы
сходимости рядов 1-3 соответственно.
Поскольку
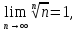 то формуле Коши-Адамара найдем
то формуле Коши-Адамара найдем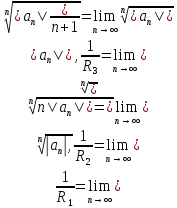 .
ОткудаR1=R2=R3.
В дальнейшем будем рассматривать
степенной ряд
.
ОткудаR1=R2=R3.
В дальнейшем будем рассматривать
степенной ряд
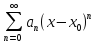 ,(4)где
числаan,
n=1,2,…,
x0.
И переменная x
принадлежат R.Пусть
R
– радиус сходимости степенного ряда
(4), тогда (x0-R;x0+R)–его
интервал сходимости.
,(4)где
числаan,
n=1,2,…,
x0.
И переменная x
принадлежат R.Пусть
R
– радиус сходимости степенного ряда
(4), тогда (x0-R;x0+R)–его
интервал сходимости.
Теорема 15. Если R>0 радиус сходимости степенного ряда (4), то внутри интервала сходимости ( xo- R; xo+R) этот ряд можно почленно дифференцировать и почленно интегрировать. При этом полученные ряды имеют тот же радиус сходимости, что и сам ряд (4), и:
 ,
где х€(
xo-
R;
xo+R).
,
где х€(
xo-
R;
xo+R).
47. Аналитические функции. Ряд Тейлора.
Если
ф-ия f(x)
аналит в т. x0€R
то в некот окрестн этой точки на действ
оси ф-ия f(x)
представима в виде степенного ряд.
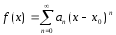 (1)
с действ.коэфan
(an€R)
(1)
с действ.коэфan
(an€R)
ОпределениеПусть
ф-я
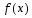 определена и имеет производные всех
пор-ков на интервале
определена и имеет производные всех
пор-ков на интервале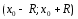 ,
тогда степенной ряд вида
,
тогда степенной ряд вида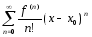 ,
наз. рядом Тейлора ф-ции
,
наз. рядом Тейлора ф-ции
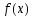 в точке
в точке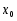
Формула
Тейлора для ф-ции f(x)
в т.
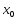


УтверждениеФ-я
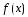 равна
сумме своего ряда Тейлора на рассматр.
инт-ле тогда и только тогда, когда в
каждой точке указанного интервала
равна
сумме своего ряда Тейлора на рассматр.
инт-ле тогда и только тогда, когда в
каждой точке указанного интервала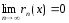
ТеоремаПусть
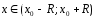 выполняются
нерав-ва
выполняются
нерав-ва
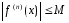 ,
гдеM>0.
Тогда имеет место
,
гдеM>0.
Тогда имеет место
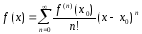 (1)
(1)
Доказательство. Согласно представлению остаточного члена формулы Тейлора в форме Лагранжа, имеем
 ,
,
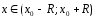
где
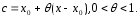
Числ.
ряд
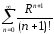 сходится по призн. Даламбера. Тогда на
основании необх. условия сходимости
ряда
сходится по призн. Даламбера. Тогда на
основании необх. условия сходимости
ряда ,
и следовательно
,
и следовательно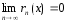 ,
,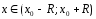 .
Поэтому,
согласно утверждению 1 имеет место (1)
.
Поэтому,
согласно утверждению 1 имеет место (1)
48. Ряды Тейлора основных элементарных функций.
Разложение в ряд функций f(x)=ex, f(x)=sin(x), f(x)=cos(x), f(x)=ln(1+x), f(x)=(1+x)α
1. Разложим в ряд функцию f (x)=ex:
Поскольку f
f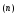 (x)=ex,
(x)=ex,
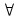 n
n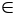 N,
то для любого фиксированого a>0,
N,
то для любого фиксированого a>0,
 x
x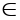 (-a;a)
выполним неравенство 0<f
(-a;a)
выполним неравенство 0<f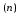 (x)<e
(x)<e .
.
Функция
e раскл. В ряд Тейлора на любом конечном
интервале, т.е. на числовой оси, а
т.к.f
раскл. В ряд Тейлора на любом конечном
интервале, т.е. на числовой оси, а
т.к.f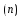 (0)=1,
то получим разложение: e
(0)=1,
то получим разложение: e =
=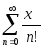 (1)
(1)
Т.к.
R=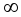 ,
то ряд абсолютно сходится на всей
числовой оси.
,
то ряд абсолютно сходится на всей
числовой оси.
2. Разложим в ряд функции f(x)=sinx и f(x)=cosx:
f(x)=sinx:
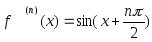 , поэтому :
, поэтому :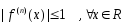 следовательно функцияsinx
раскладывается в степенной ряд на всей
числовой оси
следовательно функцияsinx
раскладывается в степенной ряд на всей
числовой оси
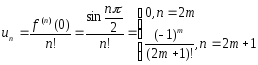
Тогда
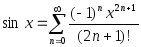 ,
,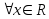 .
.
Аналогично
получаем, что
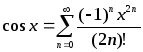 ,
,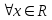 .
.
3.
Разложим в ряд
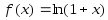 :
:
На основании теоремы о поименном интеграле степенного ряда с учётом выражения для суммы бесконечно убывающей геометрической прогрессии имеем:
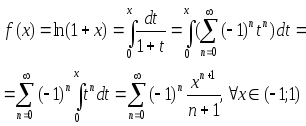
Указанный
ряд сходится попризнаке Лейбница и при
x=1.
Следовательно разложение справедливо
при x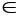 (-1;1]
(-1;1]
4.
Разложим в степенной ряд в степени
бинома
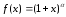 .
.
Поскольку
формула Тейлора для функции
 имеем вид:
имеем вид:
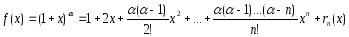
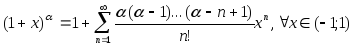
Формула Стирлинга (формула описывает асимптотическое поведение факториала n! при n→∞)
n! приn→∞
согласно опред.асимптот.равенства для
последовательностей, это означает, что
приn→∞
согласно опред.асимптот.равенства для
последовательностей, это означает, что
 =1
=1
Формулы
Эйлера определение
функций
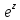 ,sin
z,
cos
z
для комплексного аргумента z
,sin
z,
cos
z
для комплексного аргумента z
cos
z =
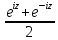 ,
sin z=
,
sin z=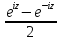 ,
,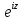 =cos
z +i sin z
=cos
z +i sin z
49.Ряды Фурье по ортонормированной системе функций.
Опр.:
Ряд вида
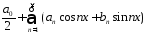 наз. тригонометрическим рядом.
наз. тригонометрическим рядом.
Теорема1:
Пусть
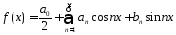 (1)
и ряд, стоящий в правой части этого
рав-ва сходится равномерно на отр-ке
(1)
и ряд, стоящий в правой части этого
рав-ва сходится равномерно на отр-ке
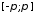 .
Тогда
.
Тогда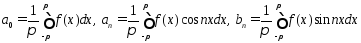 (2)
(2)
Доказательство:
Поскольку ряд, стоящий в правой части
рав-ва (1) сходится раномерно на отр-ке,
а все его члены явл. непрерывными на
этом отрезке функциями, то его сумма
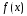 непр. на отр-ке
непр. на отр-ке ,
а сам ряд можно почленно интегрировать
от
,
а сам ряд можно почленно интегрировать
от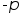 до
до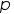 ,
т.е.
,
т.е.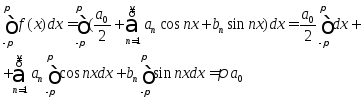
,
откуда
следует (2).
Если ряд (1) почленно умножить на
 и
и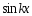 ,
то полученные ряды будут также равномерно
сходиться на отрезке
,
то полученные ряды будут также равномерно
сходиться на отрезке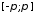 .
Интегрируя почленно эти ряды и используя
св-во ортогональности тригонометрической
системы и равенство
.
Интегрируя почленно эти ряды и используя
св-во ортогональности тригонометрической
системы и равенство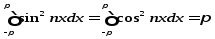 ,
получим:
,
получим: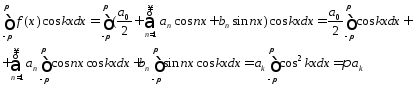
Аналогично
получим
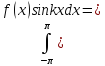 ak
ak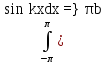 k
Из
полученных соотношений вытекают формулы
(2)
k
Из
полученных соотношений вытекают формулы
(2)
Опр.4.
Тригоном.ряд коэфф которого выражаются
по формулам (2) наз рядом Фурье, или
тригоном рядом Фурье функ f(x)
где считается, что f(x)
абсолютно интегрируема на отрезке [-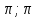 ]f(x)
]f(x)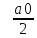 +
+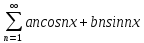
Теорема (Римана)Если функция f (x) абсолютно интегрируема на промежутке (а; b) конечном или бесконечном, то
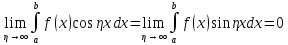
Теорема
3. Коэффициенты
Фурье абсолютно интегрируемой функции
стремятся к нулю при n
—>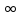 .
.
