1. Под множеством понимают совокупность определенных, вполне различных объектов, рассматриваемых как единое целое. Объекты из которых состоит множество называются элементами.

Из определения следует, что элементы множества обладают двумя свойствами: 1) вполне различимы; 2) все имеют общее свойство

Множество обозначаем :A, B, …,X, Y, Z, их элементы: a, b, …, x, y, z.

–отношение принадлежности элемента a к мн-вуA.

aA - отношение непринадлежности элемента a к мн-вуA.

Множество B называется подмножествомA , если каждый элемент множества B принадлежит множеству A (B≤A)

Множества A и Bназываются равными если они состоят из одних и тех же символов (A=B), если B≤A, B≠A, то BA, в этом случае B-собственное подмножество мн-ваA.

Не всякая совокупность объектов является множеством.

Мн-во не содержащее ни одного элемента наз. пустым (ø).ø≤A, А

Множество состоящее из конечного числа элементов ,, …,называетсяконечным. В противном случае бесконечным.

Количество элементов конечного множества называется мощностью этого множества (n=|A|) A={,, …,}

Мн-ва, равномощные мн-ву натуральных чисел наз. счетными (Ν)

Равномощные мн-ва действительных чисел континуальные (R)

Все рассматриваемые мн-ваA,B,C,…,N,RU и наз. универсальными.

Имеют место два принципа, которые играют роль аксиом: 1) принцип объемности: множества A и B наз. равными если они состоят из одних и тех же элементов.

Формой от x будем называть конечную последовательность состоящую из слов и символа x такую что если каждое вхождение x в эту последовательность заменить одним и тем же именем , то в результате получим истинное (ложное) высказывание.

2) принцип абстракции. Любая форма P(x) определяет некоторое множество A, а именно только тех элементов множества А для которых aϵA, P(a) – истинное высказывание.

В этом случае мн-во А можно задавать в виде A={x|P(x)}; A={x:P(x)}

P(x) наз. также характерным св-вом или распознающей процедурой.

Способы задания множеств: 1) перечисление A={ , , …,}; |A|=3; 2) описание характеристических свойств B={x|x=2n, nϵN}; 3) при помощи порождающей процедуры (т.е. алгоритма). Позволяет получать элементы мн-ва из уже имеющихся элементов, либо других объектов, в этом случае мн-во C содержит все объекты, которые можно получить при помощи этой процедуры

Основные операции над множествами:1. Объединением (AB) множеств A и B наз. множество AB, состоящее из всех элементов, которые принадлежат хотя бы одному из множеств A или B. AB= {x| xϵA или xϵB }. 2. Пересечение. Пересечением множеств AB называют множества A и B состоящее из тех и только тех элементов, которые принадлежат и множеству A и множеству B. AB= {x| xϵA и xϵB}; AB…C; TM…N. 3 Разностью мн-в A и B наз. мн-во A\Bсостоящее из всех элементов мн-ваAмн-вуB. A\B={x| xϵA и x неϵB }; A\BB\A. Операция всегда двуместная и некоммутативная. 4) Дополнение до универсального мн-ва U.(Ā) которое состоит из всех элементов мн-ва U не содержащихся в A. Ā=U\A=={x| xϵU и xнеϵA }. Операции объединения, пресечения и дополнения называют булевы операции над множествами.

Свойства операций:1 Коммутативность :

2 Ассоциативность :

3 Идемпотентность:

4 Дистрибутивность:

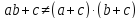
5 Законы де Моргана (отрицание).

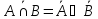
6 Инволюция (правило двойного отрицания):

2.Высказывания.Операции над высказываниями.

Высказывание-утверждение, о котором можно сказать истинно оно или ложно. Обозначается малыми (прост выск.)или большими(сложные выск.)буквами латинского алфавита.

Отрицанием высказ. а наз. высказывание ,которое принимает значение «истиности», если а-«ложно»,и принимает значение 0,если а-1,т.е. задается след табл истинности: а-0-1, а-1-0,-«отрицание а,не а,не верно, что а»

Дизъюнкцией двух высказываний называется такое новое высказывание, которое истинно тогда и только тогда, когда истинно ХОТЯ БЫ ОДНО из этих высказываний.

Конъюнкцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда истинны оба высказывания А и В.

Импликацией А => В называется высказывание, которое ложно тогда и только тогда, когда А истинно и В ложно.

Эквиваленцией двух высказываний А и В называется такое высказывание, которое истинно тогда и только тогда, когда оба эти высказывания А и В истинны или оба ложны.

3. Тождественно истинные и тождественно ложные высказывания. Равносильные высказывания.

Высказывание А(а1,..аn) наз. тождественно истинное, если оно принимает значение 1 при любых наборах истинностных значений, входящих в него прост высказывание а1,..аn. Высказывание А(а1,..аn) наз. тождественно ложное, если оно принимает значение 0 при любых наборах истинностных значений, входящих в него прост высказывание а1,..аn.

Высказывание А(а1,..аn)и В(а1,..аn)наз. равносильными, если истинностные значение этих высказываний на одинаковых наборах истинностных значений, входящих в них простейших высказываний а1,..аn совпадают.А(а1,..аn)≡В(а1,..аn).

Прим. А(а,b)=и В(а,b)=

4.Суперпозиция функций. Бинарные отношения. Свойства бинарных отношений

Суперпозицией ф-ции наз. ф-цию, полученную из системы ф-цийf, g₁,…,g_k некоторой подстановкой во внешнюю ф-цию f ф-ций g₁,…,g_k на месте её переменных и переименованиями переменных.

Например: f(x,y,z)=3x+5y²-z;

g1(x,y)=X-Y;

g1(x)=lnx;

h₁(x,z)=3(x-z)+5(x-z)²-lnz;

h₂(x,z)= 3(x-z)+5ln²(x-z)-lnz;

h₃(x,y,z,s)= 3(x-y)+5ln (y-s)²-ln(z-s);

Бинарные отношения. Свойства бинарных отношений.

Пусть задано не пустое множество 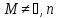– арным (n – местным) отношением на мн-ве М наз. подмн-во которое обозначатсяR(m1,m2,…,m_n), при этом говорят, что элементы (m1,m2,…,m_n) (весть спектр) находится в отношении R.

Число n наз. арностью (или местностью) отношения.

Если n=1, то говорят, что задана одноместное (унарное) отношение, а одноместное наз. св-вом или признаком мн-вом М к св-вом можно отнести эти 2 случая.

В случае n=2, отношение наз. бинарным.

Бинарное отношение - мн-во всех пар которое в общем случае.

Отношение R чаще записывают в виде aRb элементы a и b находятся в отношении R (но не на оборот).

Отношение принадлежности элементы 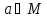также можно рассматривать как бинарное отношение между объектамиa и M, причём R(a,M), если и не принадлежностиR, если .

Бинарное отношение на конечных множествах можно представить кв. матрицей, строки и столбцы которой- элементы данного мн-ва, а элемент матрицы находящийся на пересечении строки X и столбца Y равен 1, если X и Y находятся в отношении R(XRY), и равен 0 если не находятся в отношении R. ((X,Y)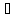R)

Запись ARB рассматривается, как совокупность всех высказываний элемента aЄA находится в отношении RaЄARbЄB.

Отрицания отношения. Пусть aRb, отношение R , бинарным отношением на мн-ве М наз. бинарное отношение в котором находятся все пары элементов мн-ва М кроме элементов находящихся в отношенииR (противоположным).

Какие бывают отношения:

1. Рефлексивным (антирефлексивным) наз. бинарное отнош. обладающим св-вом aRa

2. Симметричным наз. бинарное отнош. обладающим св-вом

3. антисимметричным наз. бинарное отнош. для которого ,

4. транзитивным наз. Бинарное отнош. R облад. св-вом

Транзитивным замкнутым бинарное отнош. Rназ.такое бинарное отношие, что, если сущ. цепочкаc₁,…c_n для которой имеет место след.нер-во aRc₁,c₁Rc₂,…,c_nRb