
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
7. Метрическое пространство . Некоторые топологические понятия
Лемма
1: Для любых действительных чисел аiи
bii=1,…,n
выполняется неравенство:
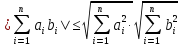
Следствие
1:
 .
.
Метрическое
пространство
 .
.
Обозначим через Rn множество всех упорядоченных наборов (x1, Х2,...,xn),xk€ R, k = 1,…, п. Каждый такой набор будем обозначать одной буквой x=(x1, Х2,...,xn) и называть точкой множества Rn. Число xk,k=1,…,пназывается k-той координатой точки x=(x1, Х2,...,xn).
Определение 1.Множество X называется метрическим пространством, если существует функция р : X ×X →R, удовлетворяющая следующим условиям:
1) p(x,y)>= 0, причем p(x,y)=0↔x=y;
2) p(x,y)=p(y,x);
3) p(x,z)<=p(x,y)+p(y,z)(неравенство треугольникa), где x,y,zпроизвольные элементы множества X.
Число
p(x,y)называется
расстоянием между точками xи
yили
метрикой пространства X.На
множестве Rn
определим расстояние между его двумя
точками x=(x1,
Х2,...,xn)и
y=(y1,
y2,...,yn)по
формуле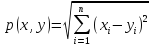 .(1)
.(1)
Функция
p:Rn×Rn→R,
определяемая формулой (1), очевидно
удовлетворяет условиям 1) и 2) определения
1. Покажем, что она удовлетворяет и
условию 3). Действительно, полагая в
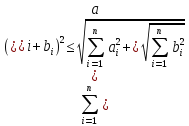 ai
= xi—
yi,
bi
= yi—
zi,
получим
условие 3) определения 1.
ai
= xi—
yi,
bi
= yi—
zi,
получим
условие 3) определения 1.
Таким образом, если на множестве Rn ввести расстояние по формуле (1), то оно превратится в метрическое пространство Rn.
Непосредственно из (1 ) следуют двойные неравенства
|xi—
yi|<=p(x,y)<=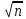 max|xk—
yk|,
i
= 1,…,n.(1<=k<=n).
max|xk—
yk|,
i
= 1,…,n.(1<=k<=n).
Определение 2. Пусть a ∈ Rn , r > 0. Множество B(a, r) = {x ∈ Rn | ρ(a, x) < r} называется открытым шаром
с центром в точке a радиуса r. Множество V (a, δ) = B(a, δ) называется δ-окрестностью точки a в множестве Rn .
Множество S = {x ∈ Rn | ρ(a, x) = r} называется сферой с центром в точке a радиуса r.
Определение 3. Пусть X ⊂ Rn . Точка a ∈ X называется внутренней точкой множества X, если существует окрестность
V (a, δ) точки a, такая, что V (a, δ) ⊂ X.
Определение
4.
Точка a ∈
Rn называется внешней точкой множества
X ⊂
Rn , если существует окрестность V (a,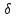 )
)
точки a, не содержащая ни одной точки из множества X.
Определение 5. Точка a ∈ Rn называется граничной точкой множества X ⊂ Rn , если любая окрестность V (a,δ) точкиa содержит как точки из множества X, так и точки не принадлежащие ему.
Определение 6. Множество X ⊂ Rn называется открытым в Rn , если каждая точка множества X является его внутренней точкой.
8.Евклидово пространство .
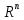 как векторное
пространство.
как векторное
пространство.
Если в Rn ввести операции сложения двух элементов x=(x1,x2, ...,xn), y=(y1,y2, ...,yn) и умножения элемента x=(x1,x2, ...,xn)на действительное число Aсоответственно по формулам:
x+y=(x1+y1,X2+y2,...,xn+ yn),
Ax=(Ax1,Ax2, ...,Axn),
то Rn станет векторным (линейным) пространством над полем действительных чисел.
Векторы ek=(0,...,0,1,0,...,0),k=1,n(1 стоит только на k-том месте) образуют линейно независимую систему векторов в пространстве Rn. Любой вектор x€ Rn можно разложить по базисным векторам ek, k=1,nв виде
x=x1e1+x2e2+...+enxn.
Норма
в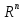 .
.
Опр1: Пусть Определение 1. Пусть X — векторное пространство. Функция || • ||: X →R, удовлетворяющая условиям
\\x\\>0,причем \\x\\=0↔x=0,
\\Ax\\= \A\.\\x\\,
\\x+y\\<=\\x\\+\\y\\(неравенство треугольника),
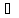 x,y€X,
x,y€X, A€R,
называется нормой в X.
Число \\x\\—
норма вектора x.Векторное
пространство Xс
введенной в нем нормой называется
векторным нормированным пространством.
В векторном пространстве Rn
определим норму по формуле ||x||=
A€R,
называется нормой в X.
Число \\x\\—
норма вектора x.Векторное
пространство Xс
введенной в нем нормой называется
векторным нормированным пространством.
В векторном пространстве Rn
определим норму по формуле ||x||= ,
гдеx=(x1,
x2,...,xn)€
,
гдеx=(x1,
x2,...,xn)€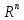 .||x-y||=p(x,y),
||x||=p(x,
0), где p(x,y)
расстояние между векторами x,y,
которые рассматриваются как точки
метрического пространства
.||x-y||=p(x,y),
||x||=p(x,
0), где p(x,y)
расстояние между векторами x,y,
которые рассматриваются как точки
метрического пространства
 .
.
Евклидова
структура в
 .Определение
2. Скалярным
произведением в действительном векторном
пространстве X
называется
функция φ:X×
X→R,
φ(x,y)=(x,y),x,y€Xи
удовлетворяющая условиям:
.Определение
2. Скалярным
произведением в действительном векторном
пространстве X
называется
функция φ:X×
X→R,
φ(x,y)=(x,y),x,y€Xи
удовлетворяющая условиям:
(x,x)>=0,(x,x)=0↔x=0,
(x,y)=(y,x),
(ax,y)=a(x,y),
(x+y,z)=(x,z)+(y,z),
 x,
y,z€X,
x,
y,z€X, a€
R.
a€
R.
В векторном пространстве Rn скалярное произведение векторов x=(x1,x2, ...,xn), y=(y1,y2, ...,yn)находится по формуле
(x,y)=x1y1+...+xnyn..
Векторное пространство Rn с определенным в нем скалярным произведением называется Евклидовым пространством.
Число
 =
= называется
длинной (модулем) вектораx=(x1,x2,
...,xn)€Rnи
обозначается |x|:|x|
=
называется
длинной (модулем) вектораx=(x1,x2,
...,xn)€Rnи
обозначается |x|:|x|
=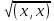 Из
вышесказанногоимеем,
что |x|=
||x||.
Иследует,
чтоp(x,y)=||x–y||
= |x–y|.
Из
вышесказанногоимеем,
что |x|=
||x||.
Иследует,
чтоp(x,y)=||x–y||
= |x–y|.
В дальнейшем, на Rn будем смотреть с одной стороны как на точечное метрическое пространство, а с другой стороны как на векторное евклидово пространство, где при этом имеет место p(x,y)=||x–y|| = |x–y|.
