
- •1.Несобственные интегралы и их свойства.
- •3. Абсолютная сходимость несобственных интегралов. Признак сравнения сходимости ни.
- •4.Предельный признак сравнения
- •6.Признак Абеля
- •7. Метрическое пространство . Некоторые топологические понятия
- •8.Евклидово пространство .
- •9. Последовательности точек пространства .
- •10. Предел отображения.
- •11. Предел по направлению. Повторные пределы.
- •12.Локальные свойства непрерывных отображений.
- •13.Глобальные свойства непрерывных отображений.
- •14. Линейные отображения.
- •15. Дифференцируемые отображения.
- •16.Свойства дифференцируемых отображений.
- •17. Достаточное условие дифференцируемости функций многих переменных.
- •18.Производная по направлению. Градиент.
- •19. Частные производные высших порядков.
- •20.Формула Тейлора для функций многих переменных.
- •21. Необходимые условия экстремума.
- •22. Достаточные условия локального экстремума.
- •23. Неявные функции.
- •24. Обратное отображение.
- •25. Необходимые условия зависимости функций.
- •26. Достаточные условия зависимости функций.
- •27. Понятие условного экстремума.
- •28. Метод множителей Лагранжа.
- •29. Числовые ряды. Критерий Коши
- •30.Признаки сравнения сходимости числовых рядов.
- •31. Признаки Даламбера и Коши сходимости рядов.
- •32. Интегральный признак сходимости ряда.
- •33. Знакочередующиеся ряды.
- •34.Признак Абеля и Дирихле.
- •35. Абсолютно и условно сходящиеся числовые ряды
- •36. Перемножение абсолютно сходящихся числовых рядов.
- •37. Бесконечные произведения.
- •38. Равномерная сходимость функциональных рядов и последовательностей.
- •39.Признаки равномерной сходимости функц. Рядов.
- •41. Непрерывность суммы ряда.
- •42.Интегрирование равномерно сходящихся рядов и последовательностей
- •43. Дифференцирование равномерно сходящихся рядов.
- •44. Степенной ряд, радиус сходимости.
- •45. Формула Коши-Адамара
- •46.Почленное дифференцирование и интегрирование степенных рядов.
- •47. Аналитические функции. Ряд Тейлора.
- •48. Ряды Тейлора основных элементарных функций.
- •49.Ряды Фурье по ортонормированной системе функций.
- •50. Интеграл Дирихле.
- •51. Сходимость рядов Фурье в точке(лемма 1)
- •52. Признак Дини и следствия из него
- •53. Суммирование рядов Фурье методом средних арифметических.
- •54. Теорема Фейера.
- •55. Теорема Вейерштрасса.
- •56. Неравенство Бесселя. Равенство Парсеваля.
- •57.Диф. Тригонометрических рядов Фурье.
- •58. Интегрирование рядов Фурье
- •59.Комплексная форма ряда Фурье.
38. Равномерная сходимость функциональных рядов и последовательностей.
Теорема
1(Критерий Коши):
Функциональная последовательность
 равномерно сходится на Е тогда и только
тогда, когда
равномерно сходится на Е тогда и только
тогда, когда
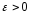 ∃
∃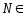 ℕ:n>N,
ℕ:n>N,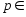 ℕ
ℕ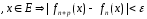 .(1)
.(1)
Док-во.
Необходимость. Пусть
 на Е. Тогда
на Е. Тогда
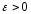 ∃
∃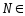 ℕ:n>N,
ℕ:n>N,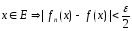
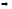
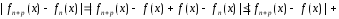
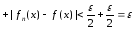 ,n>N,
,n>N, ℕ,
ℕ,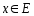
Достаточность.
Пусть имеет
место (1). Тогда при любом фиксир.
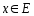 последовательность{
последовательность{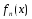 }
является числовой последовательностью,
удовлетворяющей критерию Коши, и потому
она сходится.
}
является числовой последовательностью,
удовлетворяющей критерию Коши, и потому
она сходится.
Пусть
 на Е. Покажем, что посл. {
на Е. Покажем, что посл. {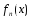 }
сходится равном.к ф-ции
}
сходится равном.к ф-ции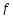 на мн-ве Е. Действительно, переходя в
(1) к пределу при
на мн-ве Е. Действительно, переходя в
(1) к пределу при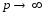 получим
получим
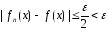 .
.
Это
и означает равномерную сходимость
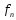 .
.
Теорема2.(Кр.Коши
равном.сход.функ.ряда) Функ ряд
 (2) равномерно
сходится на множестве Е тогда и только
тогда, когда
(2) равномерно
сходится на множестве Е тогда и только
тогда, когда 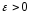 ∃
∃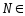 ℕ:n>N,
ℕ:n>N, ℕ,
ℕ,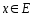 →
→
|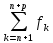 (x)|<ε
Справедливость утверждения теоремы
следует из равенства
(x)|<ε
Справедливость утверждения теоремы
следует из равенства
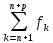 (х)=Sn+p(x)
– Sn(x)
и теоремы 1.
(х)=Sn+p(x)
– Sn(x)
и теоремы 1.
39.Признаки равномерной сходимости функц. Рядов.
Теорема
(Признак Вейерштрасса).Если
числовой ряд
 сходится и
сходится и имеет
место неравенство
имеет
место неравенство
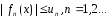 ,
то функц. ряд
,
то функц. ряд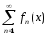 равном.сх.
на Е.
равном.сх.
на Е.
Док-во. Согл. нерав-ву, и крит. Коши сходимости числ рядов:
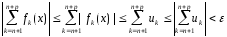
след-но , по критерию Коши равномерной сходимости функ рядов ,этот ряд сходится равномерно на Е.
Рассмотрим
функц. ряд
 (1)
(1)
Теорема(Признак
Абеля). Если
функц. ряд
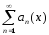 равном.
сход. на Е, а посл-ть {
равном.
сход. на Е, а посл-ть {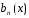 }
монотонна при каждом
}
монотонна при каждом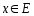 и ограничена на Е, то ряд (1) равном сход.на
Е.
и ограничена на Е, то ряд (1) равном сход.на
Е.
Теорема(Признак Дирихле). Если посл-ть част. Сумм
{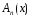 }
ряда
}
ряда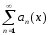 огр.
на Е, а посл.
{
огр.
на Е, а посл.
{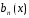 }
монотонна при каждом
}
монотонна при каждом
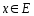 и равном. стремится к нулю на Е, то функц.
ряд (1) равном сх. на Е.
и равном. стремится к нулю на Е, то функц.
ряд (1) равном сх. на Е.
Эти призн доказ. аналогично соотв. призн. сходим.для рядов
40.
Почленный переход к пределу
Теорема6.
Если ф. ряд
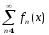 равном. сх. к суммеS(x)
на мн-ве Е, и сущ. пределы
равном. сх. к суммеS(x)
на мн-ве Е, и сущ. пределы
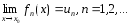 ,
то ф-цияS(x)
имеет предел в точке
,
то ф-цияS(x)
имеет предел в точке
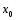 ,
причем
,
причем
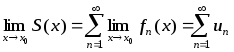 (1)
(1)
Док-во.
Согласно крит. Коши для ряда
 ,
имеем
,
имеем
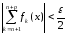 (2)
(2)
Переходя
к пределу при
 ,
получим
,
получим .
След.ряд
.
След.ряд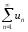 удовл. критерию Коши, а значит сх.
удовл. критерию Коши, а значит сх.
Рассм.
разность S(x)-
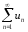 .
Т.к.S(x)=
.
Т.к.S(x)= ,
то
,
то
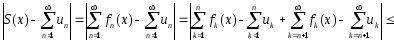
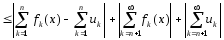 .
.
Из
равном.сходим. ряда
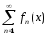 на
Е и сходим. ряда
на
Е и сходим. ряда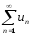 ,
заключаем, что
,
заключаем, что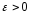 ∃
∃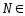 ℕ,
что
ℕ,
что
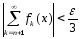 ,
и
,
и
 .
Так как предел суммы равен сумме пределов,
то для указанных
.
Так как предел суммы равен сумме пределов,
то для указанных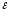 иnсущ.
иnсущ.
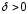 ,
что для
,
что для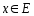 ,таких,
что
,таких,
что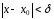 ,
выполн. нерав-во
,
выполн. нерав-во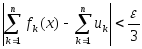
Из
сказанного имеем, что
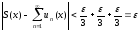 для
для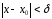 ,
а это значитS(x)
имеет предел в точке
,
а это значитS(x)
имеет предел в точке
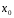 и справедливо (1).
и справедливо (1).
41. Непрерывность суммы ряда.
Теорема7.Если функции fn(x), n = 1, 2, . . . непрерывны в точке xo€ E и функциональный ряд (1.2) равномерно сходится к S(x) на E, то его сумма S(x) непрерывна в точке xo.Утверждение теоремы следует из теоремы 6, если положить, что un = fn(xo), n = 1, 2,...
Заметим, что каждой функциональной последовательности соответствует некоторый функциональный ряд, для которого она является последовательностью частичных сумм, поэтому в терминах функциональных последовательностей теоремы 6 и 7 формулируются:
Теорема
6'. Если
функциональная последовательность
{fn(x)}
равномерно
стремится к fна
Eи
для любого
n€Nсуществует
limfn(x)
= un,(x→x0)
то
предельная функция fимеет
предел в точке xo,
причем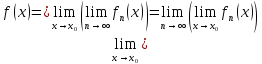
Теорема
7'. Если
функции fn(x),
n
= 1, 2,... непрерывны
в точке xo€Eи
fn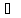 4
fна
E,
то предельная функция fнепрерывна
в точке xo.
4
fна
E,
то предельная функция fнепрерывна
в точке xo.
