
- •Міністерство освіти і науки україни
- •Частина і. Термодинаміка
- •1.1 Основи термодинаміки
- •1.1.1 Основні поняття технічної термодинаміки. Основні термодинамічні параметри. Рівняння стану.
- •1.1.2 Газові суміші
- •1.1.3 Калоричні параметри стану
- •1.1.4 Ентропія
- •1.1.4.1 Робота зміни об’єму
- •1.1.5 Робота і теплота
- •1.1.6 Перший закон термодинаміки
- •1.1.7 Теплоємність
- •1.1.8 Теплоємність металів і металовмісних сполук
- •1.1.9 Термодинамічні процеси ідеальних газів у закритих системах
- •Політропний процес
- •1.1.10 Другий закон термодинаміки
- •Цикл Карно
- •1.1.11 Формулювання другого закону термодинаміки
- •1.2 Основи хімічної кінетики
- •1.2.1 Швидкість хімічних реакцій
- •1.2.2 Вплив температури на швидкість хімічних реакцій
- •1.2.3 Хімічна рівновага
- •1.2.4 Константа рівноваги хімічної реакції залежить від температури.
- •1.3 Основи хімічної термодинаміки, поняття хімічної термодинаміки
- •1.3.1 Основи хімічної термодинаміки
- •1.3.2 Закон Гесса і його наслідки
- •1.3.3 Залежність теплового ефекту хімічної реакції від температури. Закон Кірхгофа
- •1.4 Деякі явища в рідних середовищах і на поверхні розподілу фаз
- •1.4.1 Розчинність газів
- •1.4.2 Розподіл компонента між двома рідинами
- •1.4.3 Поверхневий натяг
- •1.4.4 Адсорбція
- •1.4.5 Умова змочування і незмочування рідин
- •1.4.6 Дисоціація окисів
- •2 Теплообмін при зварюванні
- •2.1 Теплопровідність
- •2.1.1 Теплопровідність під час стаціонарного режиму і граничних умов 1 роду
- •2.1.2 Частинні випадки рівняння теплопровідності
- •Крайові умови
- •2.1.3 Теплопровідність за наявності внутрішніх джерел теплоти
- •Необмежена пластина
- •Циліндричний стержень
- •2.1.4 Необмежена плоска стінка
- •2.1.5 Циліндрична стінка
- •2.1.6 Теплопровідність під час стаціонарного режиму і граничних умовах III роду (теплопередача)
- •2.1.7 Теплопередача через плоску стінку
- •Розв'язання
- •2.2 Конвективний теплообмін
- •2.2.1 Основні поняття та визначення конвективного теплообміну
- •2.2.2 Узагальнюючі залежності (рівняння подібності) конвективного теплообміну
- •2.3 Теплообмін випроміненням
- •2.3.1 Основні поняття і визначення
- •2.3.3 Випромінення сірих тіл
- •2.3.4 Теплообмін випроміненням між твердими тілами
- •2.3.5 Теплові екрани
- •2.3.6 Випромінення газів
- •Перелік використаних і рекомендованих джерел
1.1.10 Другий закон термодинаміки
Перший закон термодинаміки не дає відповіді на питання, в якому напрямі і до якого часу проходитиме той чи інший термодинамічний процес. Інформація про напрям термодинамічного процесу випливає із другого закону термодинаміки. Для розуміння суті цього закону ми почнемо з аналізу термодинамічних циклів.
Залежно від призначення цикли бувають прямими або зворотними. Прямими називаються цикли, які використовуються для одержання роботи завдяки теплоті. Зворотні цикли призначені для перенесення теплоти від більш холодних до більш гарячих тіл. За такими циклами працюють усі холодильні машини і теплові насоси.
Процес розширення газу в циклі здійснюють вздовж шляху, який відрізняється від шляху стиснення. Процес розширення повинен відбуватися за більш високих тисків, ніж процес стиснення.
Цикли
в координатах
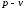 і
і зображують
замкненими кривими.
зображують
замкненими кривими.

Рисунок 1.5 – Графічне зображення циклу
Процес
підведення теплоти супроводжується
зростанням ентропії (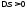 ).
Щоб повернути систему в початковий
стан, потрібно відвести деяку кількість
теплоти
).
Щоб повернути систему в початковий
стан, потрібно відвести деяку кількість
теплоти ,
внаслідок чого ентропія системи
зменшується (
,
внаслідок чого ентропія системи
зменшується (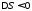 ).
Отже, кількість теплоти, що перетворюється
в циклі в роботу, дорівнює
).
Отже, кількість теплоти, що перетворюється
в циклі в роботу, дорівнює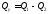 .
Значення підведеної теплоти
.
Значення підведеної теплоти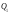 та
відведеної
та
відведеної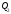 теплоти
залежить від вибраного процесу. Кількість
теплоти
теплоти
залежить від вибраного процесу. Кількість
теплоти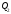 залежить
від форми шляху, яким система повертається
в початковий стан. Якщо система
повертається за кривою 2–5–1,
то
залежить
від форми шляху, яким система повертається
в початковий стан. Якщо система
повертається за кривою 2–5–1,
то
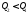 ,
якщо за 2–3–1,
то
,
якщо за 2–3–1,
то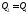 ,
за2–4–1,то
,
за2–4–1,то
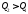 .
Лише в першому випадку в циклі може бути
отримана додатна робота.
.
Лише в першому випадку в циклі може бути
отримана додатна робота.
У
зворотному циклі робота розширення
відбувається за нижчих тисків і
температур, ніж стиснення, і робота
розширення менша, ніж робота стиснення.
Такий цикл можна здійснити, лише
затративши зовнішню роботу. Ефективність
зворотного циклу визначається холодильним
коефіцієнтом
 ,
який чисельно дорівнює відношенню
кількості теплоти, яка відбирається
від холодильного джерела
,
який чисельно дорівнює відношенню
кількості теплоти, яка відбирається
від холодильного джерела ,
до затраченої роботи
,
до затраченої роботи

Найбільш
ефективним вважається такий зворотний
цикл, коли за мінімальної затрати
зовнішньої роботи відбирається найбільша
кількість теплоти
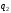 .
.
Цикл Карно
Цей цикл був розроблений в 1824 році французьким інженером С. Карно. До складу циклу входять два ізотермічні і два адіабатні процеси, які чергуються між собою. Ці процеси оборотні, лише в цьому випадку не буде відбуватися деградація теплоти.

Рисунок 1.6 – Цикл Карно
Термічний коефіцієнт корисної дії циклу Карно, як і будь-якого теплового циклу, можна знайти за формулою
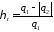
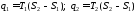
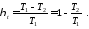
Як
бачимо, значення
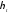 ,
залежить тільки від абсолютних температур
тепловіддавача і теплоприймача та не
залежить від властивостей робочого
тіла. Це положення дістало назву теореми
Карно.
,
залежить тільки від абсолютних температур
тепловіддавача і теплоприймача та не
залежить від властивостей робочого
тіла. Це положення дістало назву теореми
Карно.
Термічний
коефіцієнт корисної дії
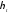 <1,
тому що
<1,
тому що
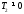 .
.
Еталоном для оцінки ефективності холодильних машин є зворотний цикл Карно, холодильний коефіцієнт якого знаходять за формулою
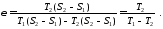
Числове
значення холодильного коефіцієнта
залежно від співвідношення
 і
і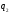 може
бути як більшим, так і меншим за одиницю.
може
бути як більшим, так і меншим за одиницю.
1.1.11 Формулювання другого закону термодинаміки
1. Формулювання другого закону термодинаміки (Р. Клазіуса)
Теплота не може самочинно переходити від менш нагрітих тіл до більш нагрітих, або некомпенсований перехід теплоти від тіла з меншою температурою до тіла з більшою температурою неможливий.
2. Формулювання У. Томсона
Теплоту будь-якого тіла неможливо перетворити в роботу, не виконуючи ніякої іншої дії, крім охолодження цього тіла.
3. Формулювання В. Освальде
Неможливо створити вічний двигун другого роду. Під вічним двигуном другого роду розуміють двигун, який міг би працювати з одним джерелом теплоти.
Щоб вивести математичний вираз другого закону термодинаміки, використаємо вирази для ККД теплових циклів.
Термічний ККД будь-якого прямого циклу визначають за формулою

Для оборотного циклу Карно за формулою
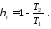
Прирівняємо ці вирази
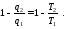
Враховуючи
те, що теплота
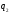 має від'ємний знак, останній вираз
перепишемо
має від'ємний знак, останній вираз
перепишемо

Величина
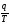 називається
зведеною теплотою. Тоді отриманий
результат можна сформулювати так:
алгебраїчна сума зведених теплот для
оборотного циклу Карно дорівнює нулю.
Цей висновок може бути поширений на
будь-який термодинамічний оборотний
цикл.
називається
зведеною теплотою. Тоді отриманий
результат можна сформулювати так:
алгебраїчна сума зведених теплот для
оборотного циклу Карно дорівнює нулю.
Цей висновок може бути поширений на
будь-який термодинамічний оборотний
цикл.

Рисунок 1.7 – До виведення математичного виразу
другого закону термодинаміки
За допомогою множини адіабат розіб'ємо цей цикл на нескінченно велике число елементарних циклів, кожний з яких складається з двох ізотерм і двох адіабат і тому є елементарним циклом Карно. Для елементарного циклу маємо
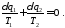
Для всього циклу можна записати

Цей вираз може бути записаним
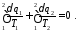
або для замкнутого контуру циклу
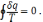
Останній вираз є математичним виразом другого закону для оборотних термодинамічних циклів.
Для необоротних циклів
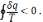
Вираз
в інтегралі Клаузіуса буде дорівнювати
нулю, якщо
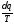 є повним диференціалом деякої функції,
яка називається ентропією
є повним диференціалом деякої функції,
яка називається ентропією
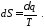
Цей вираз характеризує зміну ентропії системи, він є математичним виразом другого закону термодинаміки для оборотних термодинамічних процесів.
Розглянемо зміну ентропії в необоротних процесах. Нехай система здійснює необоротний цикл. Цей цикл складається з необоротного процесу 1-3-2 і оборотного процесу 2 - 4 -1.
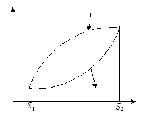
Рисунок 1.8 – Зміна ентропії в необоротних процесах
Для цього циклу інтеграл Клаузіуса має вигляд
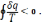
Розіб'ємо цей інтеграл на два інтеграли
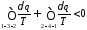
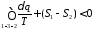
або

Продиференціювавши цей вираз, отримаємо
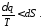
Ця нерівність є математичним виразом другого закону термодинаміки для необоротних процесів. Останнє рівняння можна записати у вигляді:

Знак рівності відноситься до оборотних термодинамічних процесів, а знак нерівності до необоротних процесів.
Об’єднаний вираз I і II законів термодинаміки
Запишемо об’єднаний вираз I і II законів термодинаміки
 (1.1)
(1.1)
Це рівняння є основним рівнянням термодинаміки. Рівняння (1.1) дає можливість установити критерії рівноваги як для ізольованих, так і неізольованих систем. Згідно з другим законом термодинаміки перехід системи до стану рівноваги відбувається самочинно і ентропія системи залишається постійною у випадку оборотних процесів або зростає якщо процеси необоротні. У стані рівноваги ентропія системи набуває максимального значення. Якщо термодинамічна система є ізольованою і однорідною, то в стані рівноваги система (U=const, V=const, а dU=0 і dV=0), тоді (1.1) набуває вигляду

Знак нерівності (1.1) характеризує системи із не рівноважного стану в рівноважний стан. В стані рівноваги

Для неізольованої системи умови рівноваги будуть залежати від характеру їх взаємодії з навколишнім середовищем. Якщо взаємодія відбувається при V=const, S=const, то dV=0, dU=0 тоді із (1.1) випливає

Звідси
випливає, що при такій взаємодії в стані
рівноваги внутрішня енергія набуває
мінімального значення. Якщо взаємодія
системи з навколишнім середовищем
відбувається при V=const
і T=const
в основному рівняння термодинаміки
член
 може
набути вигляду
може
набути вигляду
 (1.2)
(1.2)
З урахуванням (1.2) рівняння (1.1) перепишеться так:
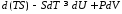
або

Ввівши позначення

де F – ізохорно-ізотермічний потенціал (вільна енергія).
Тоді рівняння (1.1) перепишеться так
 (1.3)
(1.3)
Із (1.3) виникає, що за умов взаємодії dV=0, dT=0 в системі зменшується вільна енергія

у стані рівноваги

За умов взаємодії P = const, T = const умова рівноваги набуває вигляду

де G – ізобарно-ізотермічний потенціал

Випливає, що за умов взаємодії P=const, T=const ізобарно-ізотермічний потенціал зменшується.
