1.4.4 Адсорбція

Частини твердого тіла (атомів, іонів, молекули) утворюють кристалічну гратку. У середині об’єму їх взаємодія врівноважується. На поверхні їх взаємодія не зрівноважена і поверхня твердого тіла прилягає до молекули речовини із газової фази. Явище зростання концентрації речовини на границі розподілу фаз називається – адсорбцією. Поглинаюча речовина називається – адсорбентом, а поглинута речовина – адсорбатом.

Розрізняють адсорбцію фізичну і хімічну. Фізичною називається адсорбція, яка не су­проводжується в поверхневому шарі хімічними реакціями. Якщо в результаті адсорбції утво­рюються хімічні сполуки, то така адсорбція називається хемосорбцією.

Для того щоб молекула адсорбувалась, вона повинна ударитись об поверхню і потрапити на вільне місце. Внаслідок того, що число ударів пропорційне концентрації С у довкіллі, то і ймовірність їх потрапляння на незаняте місце пропорційна цій конструкції, тобто швидкість адсорбції , тут:

-постійна;

-доля зайнятих місць на поверхні.

Молекула може десорбуватись, якщо її енергія буде достатньою, щоб відірватись від поверхні. Число таких молекул пропорційне загальному числу адсорбованих молекул і швидкість їх з поверхні .

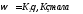У момент рівноваги

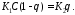
Розв’яжуючи це рівняння відносно , отримаємо

де

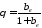Якщо позначити кількість речовини, яка адсорбується на частині поверхні черезГ, то на всій поверхні буде адсорбовано , звідкиПідставивши взамістьйого значення отримуємо рівняння ізотерми Ленгмюра.

З цього рівняння випливає, що при адсорбція досягає насичення. При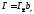, тобто адсорбція описується рівнянням Генрі.

1.4.5 Умова змочування і незмочування рідин

При достатньому збільшенні молекул між ними виникають сили зчеплення. Розрізняють між молекулярні сили когезії і адгезії . Когезією — називаються сили притягання між однако­вими молекулами. Під роботою когезії розуміють роботу розриву однофазної системи, напри­клад, стовпчика рідини з поперечним перерізом 1 см² на дві частини. При цьому утворюється нова поверхня величиною 1 см², а зміна вільної поверхні буде дорівнювати . Величина ене­ргії когезії рідин приблизно дорівнює теплоті випаровування, а твердих тіл - сублімації.

Сила притягання між різнорідними молекулами, які перебувають в різних фазах, нази­ваються - адгезією. Робота адгезії характеризується роботою, яку необхідно виконати для ві­докремлення двох фаз з площею контакту 1 см², при розділі фаз замість однієї границі і розді­лу між фазами виникали дві поверхні кожної фази. Різниця між сумою нових поверхневих енергій між фазною поверхневою енергією дорівнює роботі адгезії.

Розглянемо умови рівноваги рідини (рисунок 1.9), яка стискається з твердим тілом і га­зом на границі розділу всіх трьох фаз: рідина Р, газ Г і тверде тіло Т.

Умови розтікання або нерозтікання енергетичними співвідношеннями в системі, тобто величиною між фазної енергії, а також співвідношеннями між адгезією і когезією.

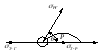
Рисунок 1.9

В точці А тангенціально до поверхні натягу діють такі сили:

- поверхневий натяг на границі рідини - газ;

- поверхневий натяг на границі тверде тіло - рідині;

- поверхневий натяг на границі тверде тіло - газ.

Сила намагається розтягнути краплю вздовж границі твердого тіла. В протилежно­му напрямі діє сила. Сила, яка діє на границі розділу газ - рідина, напрямлена по дотич­ній до поверхні краплі. Ця дотична утворює з поверхнею твердого тіла в точці зіткнення трьох фаз. Кут- називається краєвим кутом, або кутом змочування. Умова рівноваги краплі в то­чці визначають рівнянням:

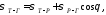
або

Це рівняння є математичним виразом закону Лапласа, який формується так: краєвий кут змочування або залежить від молекулярної природи поверхні розділу і не залежить від розмірів краплі.

Якщо вільна поверхнева енергія на границі тверде тіло-газ більша н ж на границі тверде тіло-рідина, то тверде тіло буде змочуватись рідиною.

Умову змочування можна записати:

У цьому випадку 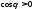і краєвий кут гострий. При,, тобто відбувається повне змочування.

Якщо на границі тверде тіло-рідина вільна поверхнева енергія більша, ніж на границі тверде тіло-газ, то рідина розділятися не буде, це можна виразити нерівністю:

При цьому і краєвий кут тупий. Крапля не розділяється і змочує поверхню твердого тіла. Повна незмочуваність характеризуєтьсяі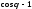.