Геометрія

∆ × Г=KL

Площини ∆ і Г – площини загального положення, а тому і лінія їх перетину – пряма загального положення.

Рішення задачі виконують Рис. 6.3 відповідно до загального алгоритму.

1.∆П2 × Гп2=K2 ∆П1 × Гп1=L1

2.K1, L1 є x

3.K2L2; K1L1 (рис. 6.3).

Якщо одна з площин займає окреме положення, то побудування лінії перетину має певні особливості.

Приклад 1. Побудувати лінію перетину двох площин ∑×∆=KL

∆┴П1, тому горизонтальна проекція лінії перетину K1L1 буде належати до ∆П1.

1. ∑П2×∆П2=K2

∑П1×∆П1=L1

2.K1L1 є ∆П1

3.L2 є x; K2L2 (рис. 6.4).

Рис. 6.4

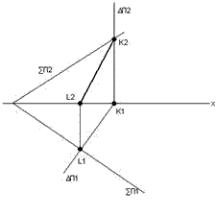Приклад 2. Побудувати лінію перетину двох площин Г×Θ.

1.Θ║П1, Θ┴П2, а тому на П2 l є Θ2

2.ГП2×l2=12

3.l1║ГП1 (рис. 6.5).

2. Перетин прямої та площини.Результатом перетину прямої та площини є

Рис. 6.5 точка.

Для побудування її проекцій необхідно:

1)Пряму заключити у допоміжну площину(проекціюючу або рівня).

2)Побудувати лінію перетину прямої та заданої площин

3)Позначити точку перетину лінії перетину двох площин та заданої прямої.

Приклад. Побудувати точку перетину прямої та площини.

1. l є ∑; ∑┴П2

2. ∑2×Г(ABC)=1,2

∑2×A2C2=12

∑2×B2C2=22

3. 11 є A1C1

21 є B1C1

4.1121×l1=K1

5.K2 є l2 (рис. 6.6).

Рис. 6.6

Контрольні питання.

1.Як побудувати лінію перетину двох площин, заданих плоскими геометричними фігурами?

2.Як побудувати лінію перетину двох площин, заданих слідами?

3.Як побудувати точку перетину прямої та площини?

4.Як визначити елементи видимості пересічних площин, прямої та площини?

27.

У будь-якій площині, яка не паралельна і не перпендикулярна до площин проекцій, існують особливі лінії, іноді їх називають головними лініями. Це лінії, що належать площині і паралельні площинам проекцій (лінії рівня), а також прямі, які належать площині і перпендикулярні до її ліній рівня (лінії найбільшого нахилу площини до площин проекцій). Лінія, що належить площині і паралельна горизонтальній Рис.3.6

площині проекцій, називається

горизонталлю площини. Лінія, яка належить площині і паралельна фронтальній площині проекцій, називається фронталлю площини. Профільна пряма площини – це пряма площини, яка паралельна профільній площині проекцій. На рис. 3.6 у площині Q(Δ DGH) побудовано фронталь f(f1, f2), горизонталь h(h1, h2) і лінію G3(G131, G232) найбільшого нахилу площини Q до горизонтальної площини проекцій, інакше вона ще називається лінією найбільшого схилу (G131^ h1). Кут нахилу лінії найбільшого нахилу площини до відповідної площини проекцій дорівнює куту нахилу площини до цієї площини проекцій. Наприклад, кут нахилу лінії G3 до горизонтальної площини проекцій (рис. 3.6) дорівнює куту нахилу площини Q до площини П1.

Слід зауважити, що лінія найбільшого нахилу площини може бути її визначником, тобто площина може бути задана на кресленні відповідною лінією найбільшого нахилу.

Лінії рівня часто використовуються для розв’язування різноманітних задач. Їх, наприклад, зручно використовувати для побудови точок у площині. На рис. 3.7 показано три можливі схеми побудови фронтальної проекції А2 точки А, що належить площині Σ(f0; h0), за її заданою горизонтальною проекцією: Рис. 3.7

за допомогою

прямої загального положення 12(1121, 1222), горизонталі h(h1, h2) або фронталі f(f1, f2).

Площини, які було розглянуто на всіх попередніх ілюстраціях, не

перпендикулярні до жодної із площин проекцій. Такі площини називаються площинами загального положення. Проекції площин загального положення збігаються з полями відповідних площин проекцій. Тому некоректно говорити про проекції конкретних площин загального положення при розв’язуванні задач, пов’язаних із ними. Тут доцільно говорити про проекції визначника, яким задається площина.

Якщо площина задається слідами, то кут між її слідами може бути гострим чи тупим. Якщо площина загального положення утворює однакові кути з площинами П1 та П2, то її фронтальний і горизонтальний сліди на кресленні утворюють однакові кути з віссю х12, зокрема, можуть збігатися, а профільний слід нахилений до осі y3 під кутом 45°

28. Якщо у способі заміни площин проекцій геометричні образи є зафіксованими у просторі, а до них певним чином проводять нові площини проекцій, то у способі обертання все відбувається

навпаки. Основні площини проекцій p1 та p2вважаються зафіксованими у просторі, а геометричні образи обертаються певним чином, щоб перевести їх із загального положення в особливе (окреме) і вигідне для розв’язку поставленої задачі.

Осі обертання інколи задаються в умові задачі, а часом їх треба вибрати самостійно. Якщо є можливість вибору положення осі, то її доцільно розміщуватиперпендикулярно до однієї з площин проекцій, що спрощує побудову.

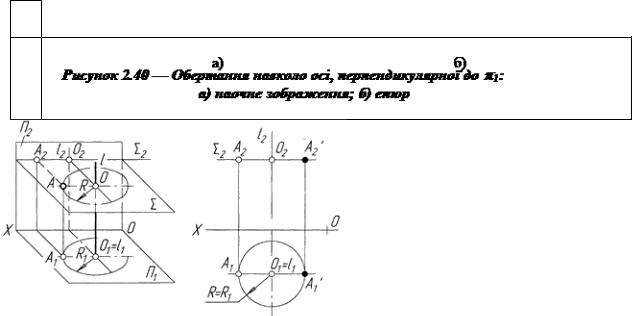
На рисунку 2.40 бачимо, що площина обертання є паралельною до тієї площини проекцій, до якої вісь обертання - перпендикулярна. Завдяки цьому коло, що описує точка А при обертанні в площині обертання, буде проектуватися на одну з площин проекцій у коло, а на дві інші – у відрізок, що дорівнює діаметру кола і лежить на слідах площин обертання .

На перетині площини обертання Σ і осі обертання l дістаємо точку О – центр обертання. Радіус обертання R дорівнює відстані між точками А і О. Побудова епюра зводиться до проведення на площині p1 кола радіусом R=R1 з центра О1 і на площині p2 відрізка прямої довжиною 2R, який співпадає із слідом Σ2, паралельним до Х.

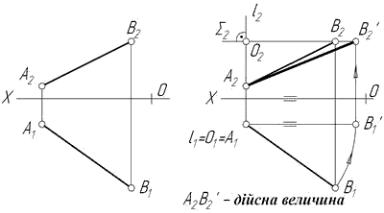
Обертанням навколо довільно вибраної осі l, перпендикулярної до площини p1, визначити дійсну величину відрізка АВ (рис.2.41).

Відомо, що пряма, паралельна до площини проекцій, проектується на цю площину в дійсну величину. Отже, повернувши

відрізок АВ у положення, паралельне до площини p2, дістанемо нову фронтальну проекцію відрізка А2В′2, яка буде його дійсною величиною. Для цього позначаємо необхідні елементи обертання для точки В, виходячи з того, що вісь обертання проходить через точку А і перпендикулярна до p1. Нове положення точки В′1 знайдемо за правилами, описаними вище. Нагадаємо, що А1В′1=А1В1. Проведемо лінію проекційного зв’язку з точки В′1 до перетину з Σ2 і знайдемо точку В′2, яку сполучимо з точкою А2. Фронтальна проекція А2В′2 відрізка АВ після обертання є його дійсною величиною, тобто А2В′2=АВ.

Рисунок 2.41

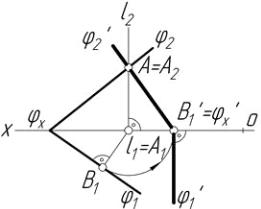
Задача 26 Знайти дійсну величину трикутника АВС (рис.2.42)

Враховуючи, що вершина трикутника, точка А, лежить у площині p1, вибираємо вісь

обертання l, щоб вона прходила через точку А перпендикулярно до площини p2. При обертанні трикутника АВС точка А залишається на місці, а точки В і С, обертаючись у площинах, перпендикулярних до l, займуть нове положення В′1 і С′1, тобто сумістяться з площиною p1. Таким чином, після обертання всі три точки А, В, С – вершини трикутника будуть лежати в площині p1, а отже А1В′1С′1 – дійсна величина трикутника АВС.

Рисунок 2.42

Задача 27 Повернути довільну площину j до положення фронтально-проекційної площини (рис.2.43).

Рисунок 2.43

Відомо, що фронтально-проекційна площина має горизонтальний слід перпендикулярний до осі проекцій ОХ. Щоб досягти такого положення сліду j1, вибираємо вісь обертання l так, щоб ваша була перпендикулярна до площини проекцій p1 і лежала у площині p2. Тому вона перетинає слід j2 в точці А, яка залишаєтиься нерухомою і належить новому фронтальному сліду j2 площини j. У даному випадку можливі два розв’язки: поворот за годинниковою стрілкою і проти.

Розглянуті вище положення і задачі стосуються найпростішого випадку обертання навколо осей, перпендикулярних до будь-якої з площин проекцій. Порівняно складніше обертання навколо осей, паралельних до однієї із площин проекцій, тобто навколо лінії особливого положення – горизонталі або фронталі, або навколо одного із слідів площини, що є нульовою горизонталлю або фронталлю.

Обертання навколо прямої рівня. Цей спосіб застосовується в тих випадках, коли плоску фігуру, відрізок прямої або плоску криву потрібно сумістити з площиною, яка паралельна одній з площин проекцій. Тоді плоска фігура, крива або відрізок прямої будуть проектуватися на відповідну площину проекцій без спотворення.

Задача 28 Знайти дійсну величину трикутника АВС навколо горизонталі (рис.2.44).

Горизонталь, яка служить віссю обертання, проведення через вершину трикутника А, тому остання під час обертання залишається нерухомою. Другою нерухомою точкою площини трикутника АВС буде точка 1, перетин горизонталі з стороною ВС трикутника.

Зрозуміло, що побудова нового положення площини при обертанні її навколо горизонталі або фронталі зводиться, як і в інших випадках, до обертання окремих точок або прямих, що лежать у даній площині.

На рисунку 2.44,б, в знаходимо нове положення точки С, провівши через неї площину обертання S перпендикулярно до осі обертання, знаходимо дійсну величину радіуса обертання (способом прямокутного трмкутника) і знаходимо С0. нове положення точки В – В0 знаходимо в місці перетину траекторії руху точки В (горизонтально проекційна площина d з напрямком нового положення сторони трикутника С0С1. З’єднавши АВ0С0 – знаходимо дійсну величину трикутника АВС.

Рисунок 2.44

29. Нехай ми маємо якийсь об’єкт, наприклад, точку А, яка спроекційована на дві площини проекцій П1 та П2 (рис. 6.4). З якоїсь причини нас не влаштовують проекції А1 і А2. Необхідно перетворити креслення, замінивши одну з площин проекцій, наприклад, П2. Введемо нову площину П4, перпендикулярну до площини П1. При цьому утворилась нова система

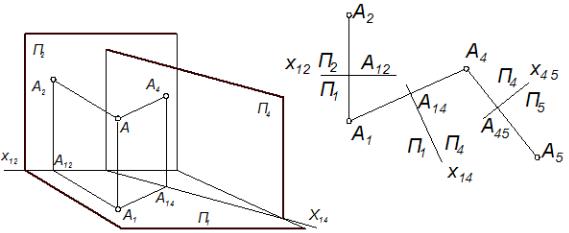площ ин проекцій П1/П4 з новою віссю проекцій x14. Спроекціюємо ортогонально точку А на нову площину проекцій, маємо проекцію А4. Звернімо увагу на те, що висота ZA точки А однаково без спотворення проек

Рис. 6.4 Рис. 6.5

ціюється і на площину П2 («стару») і на площину П4 («нову»). Ця обставина і використовується для побудови нової проекції А4.

Суть способу заміни площин проекцій полягає у заміні однієї площини проекцій іншою, перпендикулярною до тієї, що залишається. У такому разі від старої системи площин проекцій П1/П2 залишається одна площина проекцій і все, що з нею пов’язане, а саме проекція предмета на цю площину і відстані від точок предмета до цієї площини.