1.3. Шенноновский подход к определению количества информации

Синтаксический подход к определению информации развивается в статистической теории информации. Шенноном было введено понятие количества информации как меры неопределенности состояния системы, снимаемой при получении информации. Количественная мера неопределенности состояния называется энтропией. При получении информации уменьшается неопределенность, то есть энтропия системы. Получение информации связано с изменением степени неосведомленности получателя о состоянии системы.

Если система Х обладает дискретными состояниями, то есть может переходить из состояния в состояние скачком, их количество равно N, а вероятность нахождения системы в каждом состоянии p₁, p₂, … ,p_N , p_i = 1, p_i 1, то энтропия системы равна

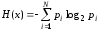
Если после получения сообщения энтропия, то есть неопределенность состояния системы, стала 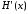, то количество информации равно

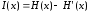
Таким образом, количество информации измеряется уменьшением неопределенности состояния системы. Энтропия H равна нулю только когда все вероятности p_i, кроме одной, равны нулю, а эта единственная вероятность равна единице. Таким образом, 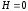только в случае полной определенности состояния системы.

При заданном числе состояний системы N энтропия максимальна когда все p_i равны между собой и равны

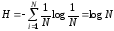
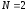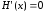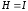Пусть система имеет два равновероятных состояния, то есть . Будем считать, что снятие неопределенности о состоянии такой системы дает одну единицу информации. При полном снятии неопределенностии. Тогда

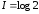
Эта величина принимается за единицу информации, называемую бит. В общем случае при N равновероятных состояний количество информации будет равно

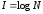
Информация передается в виде сообщений, которые можно представить в виде кодовых комбинаций символов некоторого алфавита, содержащего m символов. Если используются n-разрядные коды, то количество кодовых комбинаций будет

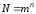
Тогда количество информации в сообщении будет

.

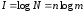Описание любого события или объекта формально можно рассматривать как указание на то, в каком из возможных состояний находится описываемый объект. Тогда протекание событий во времени есть не что иное, как смена состояний, выбранных из числа всех возможных. Чем выше уровень неопределенности выбора, тем большую степень неожиданности имеет результат выбора и тем большую информацию он несёт. Поэтому в теории информации количество информации является мерой снятия неопределенности.

1.4. Ценность информации

Статистический метод определения количества информации не учитывает её ценность. Одна и та же информация для различных получателей может иметь разную ценность. Для понимания и использования информации её получатель должен обладать определенным запасом знаний. Полное незнание предмета не позволяет извлечь существенную информацию из принятого сообщения об этом предмете.

Для оценки смыслового значения информации используется понятие тезауруса. В общем смысле тезаурус – это совокупность знаний, накопленных человеком или некоторым коллективом. Понятие тезауруса применимо не только к социальным системам, но и к любым сложным системам. Тезаурус – это полезная внутренняя информация системы о себе и внешней среде, которая определяет способность системы распознавать ситуацию и управлять своим поведением. Таким образом, тезаурус является информационным самоотображением сложной системы. Это информационный ресурс системы, определяющий степень её организованности.

Количество информации, содержащейся в некотором сообщении, можно оценить степенью изменения индивидуального тезауруса под воздействием данного сообщения. Иными словами, количество информации, извлекаемой получателем из поступающих сообщений, зависит от степени подготовленности его тезауруса для восприятия такой информации. Если индивидуальный тезаурус получателя сообщения близок нулю, то получатель не понимает сообщение и для него количество принятой информации равно нулю. Такая ситуация аналогична прослушиванию сообщения на неизвестном языке. Несомненно, что сообщение не лишено смысла, однако оно непонятно, а значит, не информативно. Количество информации в сообщении также будет равно нулю, если его получатель знает абсолютно всё о предмете. В этом случае сообщение не дает ему ничего нового.