+_Algebra10_Nelin_profil

84  Розділ 1. ФУНКЦІЇ, МНОГОЧЛЕНИ, РІВНЯННЯ І НЕРІВНОСТІ

3.2. системи рівнянь

§ 3. Рівняння та їх системи  85

Продовження табл. 11

3. Рівносильність систем рівнянь

Означення

Найпростіші властивості рівносильних систем

1.Якщо змінити порядок запису рівнянь заданої системи, то одержимо систему, рівносильну заданій.

2.Якщо одне з рівнянь системи замінити на рівносильне йому рівняння, то одержимо систему, рівносильну заданій.

3.Якщо в системі рівнянь з одного рівняння виразити одну змінну через інші та одержаний вираз підставити замість цієї змінної в усі інші рівняння системи, то одержимо систему, рівносильну заданій.

4.Якщо якесь рівняння системи замінити сумою цього рівняння, помноженого на число α ≠ 0, і якогось іншого рівняння, помноженого на число β ≠ 0, то одержимо систему, рівносильну заданій.

4. Основні способи розв’язування систем рівнянь

Спосіб підстановки

Виражаємо з одного рівняння системи одну змінну через іншу (чи через інші) і підставляємо одержаний вираз замість відповідної змінної у всі інші рівняння системи (потім розв’язуємо одержане рівняння чи систему і підставляємо результат у вираз для першої змінної).

2x−y =3,

Приклад. Розв’язати систему

x+ y =3.

Р о з в’я з а н н я. З першого рівняння системи у = 2х – 3. Підставляємо в друге рівняння системи та одержуємо х + 2х – 3 = 3. Звідси х = 2. Тоді у = 2х – 3 = 1.

Відповідь: (2; 1).

Спосіб додавання

Якщо перше рівняння системи замінити сумою першого рівняння, помноженого на число α ≠ 0, і другого рівняння, помноженого на число β ≠ 0 (а всі інші рівняння залишити без зміни), то одержимо систему, рів-

носильну заданій.

86  Розділ 1. ФУНКЦІЇ, МНОГОЧЛЕНИ, РІВНЯННЯ І НЕРІВНОСТІ

Продовження табл. 11

Розв’язання. Помножимо обидві частини першого рівняння системи на 2, а другого — на 3 (щоб одержати як коефіцієнти при змінній у протилежні числа) і почленно додамо одержані рівняння. З одержаного рівняння знаходимо значення х, підставляємо результат у будь-яке рівняння системи та знаходимо значення у.

10x−6y =18,

9x+6y =39. + 19x =57,

x =3.

Тоді 3•3 + 2у = 13, 2у = 4, у = 2

Відповідь: (3; 2).

Спосіб заміни змінних

Перетворюємо задану систему так, щоб всі рівняння системи були записані через однакові вирази зі змінними, і ці вирази замінюємо новими змінними.

Розв’язання. Оскільки до запису рівнянь заданої системи змінні вже

рівняння останньої системи на ( –2) і почленно додавши результат до дру-

що пара (2; 2) є розв’язком заданої системи.

Відповідь: (2; 2).

§ 3. Рівняння та їх системи  87

Продовження табл. 11

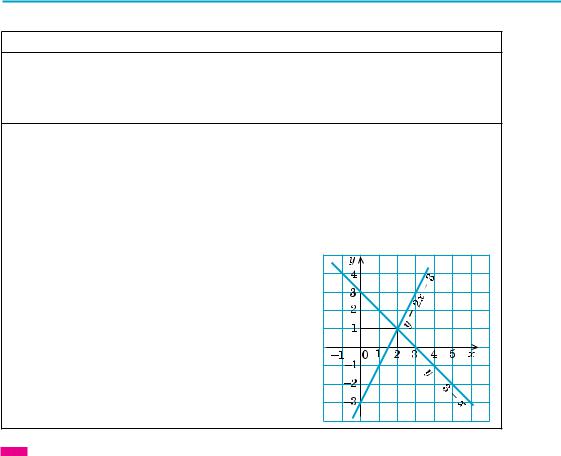
5. Графічне розв’язування систем рівнянь з двома змінними

Виконуємо рівносильні перетворення заданої системи так, щоб зручно було будувати графіки всіх рівнянь, що входять до системи. Потім будуємо відповідні графіки і знаходимо координати точок перетину побудованих ліній — ці координати і є розв’язками системи.

2x−y =3,

Приклад. Розв’язати графічно систему

x+ y =3.

y =2x−3,

Розв’язання. Задана система рівносильна системі

y =3−x.

Графіком кожного з рівнянь системи є пряма.

Для побудови прямої досить побудувати дві її точки. Наприклад, для

Графіки перетинаються в єдиній точці М (2; 1). Отже, пара чисел (2; 1) — єдиний розв’язок заданої системи.

Відповідь: (2; 1).

Пояснення й обґрунтування

З поняттям системи рівнянь, її розв’язку та з основними методами розв’язування систем рівнянь, поданими в таблиці 11, ви знайомі з курсу алгебри 7–9 класів. Повністю аналогічно до відповідних понять, пов’язаних з рівняннями, вводиться поняття області допустимих значень системи рівнянь (див. пункт 3 табл. 11), поняття систем-наслідків (пункт 2 табл. 11) та рівносильних систем (пункт 3 табл. 11).

Як і для рівнянь з означення системи-наслідку:

якщо кожний розв’язок першої системи рівнянь є розв’язком другої системи, то друга система називається наслідком першої,

одержуємо такий орієнтир: для одержання системи-наслідку достатньо

розглянути задану систему рівнянь як систему правильних числових рівностей i гарантувати (тобто мати можливість обґрунтувати), що кожну наступну систему рівнянь ми можемо одержати як систему правильних числових рівностей.

90  Розділ 1. ФУНКЦІЇ, МНОГОЧЛЕНИ, РІВНЯННЯ І НЕРІВНОСТІ

Продовження табл. 12

3. Використання зростання та спадання функцій

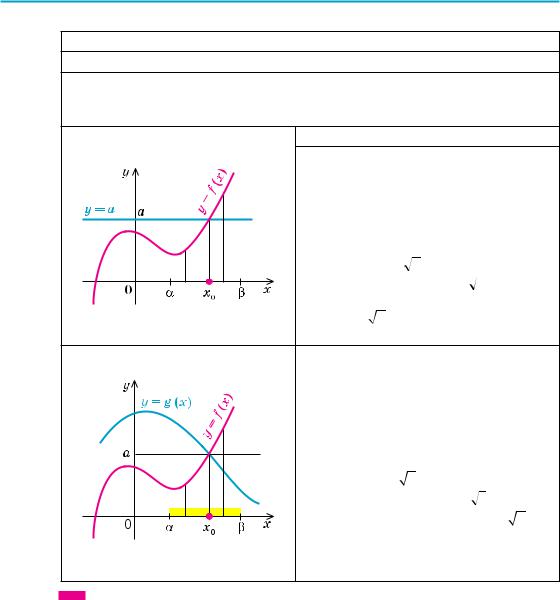
Схема розв’язування рівняння

1. Підбираємо один або декілька коренів рівняння.

2. Доводимо, що інших коренів це рівняння не має (використовуючи теореми про корені рівняння або оцінку лівої та правої частин рівняння)

Теореми про корені рівняння

1. Якщо в рівнянні f (x) = a функція f (x) зростає (спадає) на деякому проміжку, то це рівняння може мати не більш ніж один корінь на цьому проміжку.

2. Якщо в рівнянні f (x) = g (x) функ-

ція f (x) зростає на деякому проміжку, а функція g (x) спадає на цьому самому проміжку (або навпаки), то це рівняння може мати не більш ніж один корінь на цьому проміжку.

Приклад

тобто 2 = 2), оскільки f (x) = x +x3 зростає на всій області визначення х l 0, а g (x) = 3 – х спадає (на множині R, а отже, і при x l 0)

Пояснення й обґрунтування

1. Скінченна ОДЗ. Нагадаємо, що у разі, коли задано рівняння f (x) = g (x), спільна область визначення для функцій f (x) і g (x) називається областю допустимих значень цього рівняння. Зрозуміло, що кожен корінь заданого рівняння входить як до області визначення функції f (x), так і до області визначення функції g (x). Отже, кожен корінь рівняння