+_Algebra10_Nelin_profil
.pdf
Розділ 2
СТЕПЕНЕВА
ФУНКЦІЯ
§ 9. Корінь n-го степеня та його
властивості. Функція 
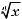та її графік
§10. Ірраціональні рівняння
§11. Ірраціональні нерівності
§12. Узагальнення поняття степеня. Степенева функція, її властивості та графік
§13. Розв’язування ірраціональних рівнянь та нерівностей з параметрами
³ ЦЬОМУ РОЗД Л ВИ ОЗНАЙОМИТЕСЯ З УЗАГАЛЬНЕННЯМ ПОНЯТТЯ КВАДРАТНОГО КОРЕНЯ x КОРЕНЕМ Q ГО СТЕПЕНЯ ТА ЙОГО ВЛАС ТИВОСТЯМИ НАВЧИТЕСЯ РОЗВsЯЗУВАТИ РРАЦ ОНАЛЬН Р ВНЯННЯ ТА БУДУВАТИ ГРАФ КИ СТЕПЕНЕВИХ ФУНКЦ Й ФУНКЦ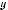 
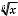ВИКОРИСТОВУВАТИ Х ВЛАСТИВОСТ ДО РОЗВsЯЗУВАННЯ Р ЗНОМА Н ТНИХ ЗАДАЧ ¢И ОЗНАЙОМИТЕСЯ З МЕТОДАМИ РОЗВsЯЗУВАННЯ Б ЛЬШ СКЛАДНИХ ЗАВДАНЬ З ТЕМИ ЯК ПРОПОНУЮТЬ У ЗАВДАН НЯХ ЗОВН ШНЬОГО НЕЗАЛЕЖНОГО ОЦ НЮВАННЯ ЧИ ДЕРЖАВНО П ДСУМКОВО АТЕСТАЦ З МАТЕМАТИКИ ЦЕ ПЕРШ ЗА ВСЕ МЕТО ДИ РОЗВsЯЗУВАННЯ РРАЦ ОНАЛЬНИХ НЕР ВНОСТЕЙ ЗАСТОСУВАННЯ ВЛАСТИВОСТЕЙ ФУНКЦ Й ДО РОЗВsЯЗУВАННЯ РРАЦ ОНАЛЬНИХ Р В НЯНЬ ТА МЕТОДИ РОЗВsЯЗУВАННЯ РРАЦ ОНАЛЬНИХ Р ВНЯНЬ НЕ Р ВНОСТЕЙ З ПАРАМЕТРАМИ
162 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
§ 9 |
КОРІНЬ n-го СТЕПЕНЯ ТА ЙОГО ВЛАСТИВОСТІ. |
ФУНКЦІЯ y= n x ТА ЇЇ ГРАФІК |
9.1.Корінь n-го степеня та його властивості. Перетворення виразів з корeнями n-го степеня
|
Таблиця 18 |
|
|
1. Означення |
|
Квадратний корінь |
Корінь n-го степеня |
Квадратним коренем із числа a |
Коренем n-го степеня з числа a нази- |
називається таке число b, квадрат |
вається таке число b, n-й степінь якого |
якого дорівнює a. |
дорівнює a. |
Якщо a = b2, то b — квадратний |
Якщо a = bn (n N, n ≠ 1), то b — |
корінь із числа a. |
корінь n-го степеня з числа a. |
|
|
Арифметичний корінь — невід’ємне значення кореня.
При a l 0: a, n a — позначення арифметичного значення кореня.
|
|
|
|
|
|
|
( a)2 = a |
|
|
(n a)n = a |
|
|
|
|
|
|
|
|
2. Область допустимих значень (ОДЗ) |
||||
Квадратний корінь |
Корінь n-го степеня |
||||
a існує тільки при а l 0 |
2k a існує тільки при а l 0 (k N); |
||||
2k+1 a існує при будь-яких значеннях а |
|||||
Запис розв’язків рівняння хn = a (n N)
п = 2k + 1 — непарне (k N) |
|
п = 2k — парне (k N) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
При будь-яких значеннях a |
|
При a < 0 |
При a l 0 всі корені |
|||||||
рівняння х2k + 1 = а має єдиний |
|
рівняння x2k = a |
||||||||
|
корінь x = 2k+1 a |
|
рівняння x2k = a |
можна записати |
||||||
|
|
не має коренів |
||||||||
|
|
|
|
так: x = ±2k a |
||||||
|
|
|
|
|
|
|||||
|
|
|
Приклади |
|
|
|
|
|
||
Рівняння х5 = 3 має єдиний |
|
Рівняння х8 = –7 |
Рівняння х8 = 7 |
|||||||
|
корінь x = 5 3 |
|
не має коренів |
має корені x = ±8 7 |
||||||
|
3. Властивості кореня n-го степеня |
|
|
|
|
|
||||
п = 2k + 1 — непарне число |
|
п = 2k — парне число |
||||||||
|
|
|
|
|
|
|
|
|
|
|
1) 2k+1 −a = −2k+1 a |
|
|
|
|
|
|
|
|
||
|
|
n an = 2k a2k = |
|
a |
|
|
||||
2) |
n an = 2k+1 a2k+1 = a |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
§ 9. Корінь n-го степеня та його властивості. Функція y = n x та її графік 163 |
||||
|
|
|
|
Продовження табл. 18 |
|
Для довільних значень п і k (n N, n ≠ 1, k N) |
|||||
3) |
При а l 0 |
n k a = nk a |
|||
4) |
При а l 0 |
(n a)k = n ak |
|||
5) |
При а l 0, b l 0 |
n ab = n a æ n b |
|||
|
Наслідки |
|
|||
При а l 0, b l 0 n anb = an b — вине |
При а l 0, b l 0 an b = n anb — вне |
||||
сення множника зпід знака кореня. сення множника під знак кореня. |
|||||
6) |
При а l 0, b > 0 |
n a |
= |
n a |
|
b |
n b |
||||
|
|
|
|||
7) |
При а l 0 n am =nk amk |
— основна властивість кореня |
|||
Значення кореня зі степеня невід’ємного числа не зміниться, якщо по- |
|||||
казник кореня і показник степеня підкореневого виразу помножити (або |
|||||
поділити) на одне й те саме натуральне число. |
|||||
8) |
При a l 0, b l 0, |
якщо a > b, то n a > n b |
|||
|
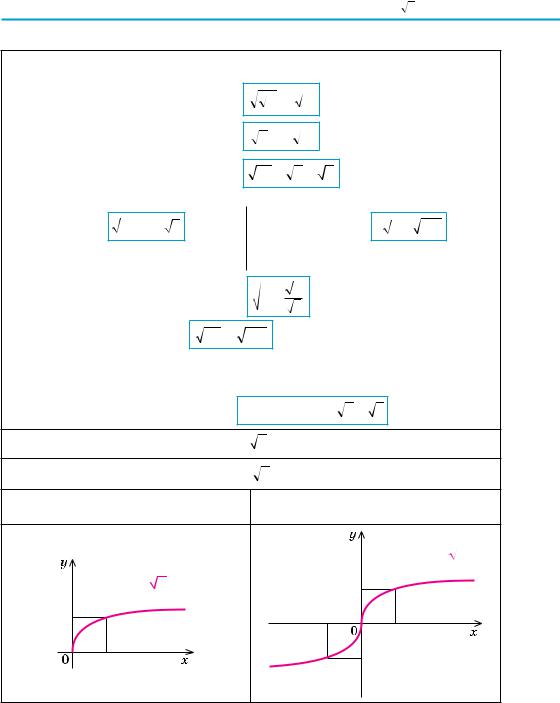
4. Функція y = n x та її графік |
||||
|
Графік функції y = n x (n N, n l 2) |
||||
n — парне (n = 2k, k N) |
|
n — непарне (n = 2k +1, k N) |
|||
|
|
|
|
y = 2k+1 x |
|
|
y = 2k x |
|
|
1 |
|
|
|
|
|
||
1 |
|
|
|
–1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
–1 |
|
|
|
|
|
||
164 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
|
|
|
Продовження табл. 18 |
||
|
|
|
|
|
|
Властивості функції y = n x |
|
|
|
||
n — парне (n = 2k, k N) |
n — непарне (n = 2k +1, k N) |
||||
1. Область визначення: x l 0, |
1. Область визначення: x R (x — |
||||
тобто |
будь-яке дійсне число), тобто |
||||
D (2k x) =[0;+∞). |
|
D (2k+1 x)= R. |
|||
2. Область значень: у l 0, тобто |
2. Область значень: у R (у — будь- |
||||
E(2k x) =[0;+∞). |
яке дійсне число ), тобто |
||||
|
|
E(2k+1 x)= R. |
|||
3. Найбільшого значення функція |
3. Найбіль ого і наймен ого зна- |
||||
y =2k x не має; найменше значення — |
чень функція y =2k+1 x не має. |
||||
у = 0 (при х = 0). |
|
|
|
|
|
|
|
|
|||
4. Функція ні парна, ні непарна. |
4. Функція непарна: |
2k+1 −x = −2k+1 x, |
|||
отже, графік функції симетричний |
|||||
|
відносно початку координат. |
||||
|
|
|
|
||
|
x =0, |
Оx |
y =0, |
||
5. Точки перетину з осями координат: Оy |
|
|
|||
|
y =0; |
|
x =0. |
||
Графік проходить через початок координат. |
|||||
6. Проміжки зростання і спадання: на всій області визначення |
|||||
функція зростає. |
|
|
|
|
|
|
|
||||
7. Проміжки знакосталості: |
7. Проміжки знакосталості: |
||||
при х > 0 значення у > 0, |
|||||
при х > 0 значення у > 0 |
|||||
при х < 0 значення у < 0 |
|||||
|
|||||
Пояснення й обґрунтування
1. Означення кореня п-го степеня. Поняття кореня квадратного з числа а вам відомо: це таке число, квадрат якого дорівнює а. Аналогічно означають і корінь п-го степеня з числа а, де п — довільне натуральне число, біль е за 1.
Коренем п-го степеня з числа а називається таке число, п-й степінь якого дорівнює а.
Наприклад, корінь третього степеня з числа 27 дорівнює 3, оскільки 33 = 27; корінь третього степеня з числа –27 дорівнює –3, оскільки (–3)3 = –27. Числа 2 і –2 є коренями четвертого степеня з 16, оскільки 24 = 16 і (–2)4 = 16.
При п = 2 та при п = 3 корені п-го степеня називають також відповідно квадратним та кубічним коренями.
§ 9. Корінь n-го степеня та його властивості. Функція y = n x та її графік 165
Як і для квадратного кореня, для кореня п-го степеня вводять поняття арифметичного кореня.
Арифметичним коренем п-го степеня з числа а називається невід’ємне число, п-й степінь якого дорівнює а.
При а l 0 для арифметичного значення кореня п-го степеня з числа а існує спеціальне позначення1: n a; число n називають показником кореня, а саме число a — підкореневим виразом. Знак n і вираз n a називають також радикалом.
Наприклад, те, що корінь третього степеня з числа 27 дорівнює 3, записують так: 3 27 =3; те, що корінь четвертого степеня із 16 дорів-
нює 2, записують так: 4 16 =2. Але для запису того, що корінь четвертого степеня із 16 дорівнює –2, позначення немає.
При а < 0 значення кореня п-го степеня з числа а існує тільки при непарних значеннях п (оскільки не існує такого дійсного числа, парний степінь якого буде від’ємним числом). У цьому випадку корінь непарно-
го степеня п із числа а теж позначають n a. Наприклад, те, що корінь третього степеня з числа –27 дорівнює –3, записують так: 3 −27 = −3. Оскільки –3 — від’ємне число, то 3 −27 не є арифметичним значенням кореня. Але корінь непарного степеня з від’ємного числа можна виразити через арифметичне значення кореня за допомогою формули
2k+1 −a = −2k+1 a .
Щоб довести наведену формулу, зауважимо, що за означенням кореня п-го степеня ця рівність буде правильною, якщо (−2k+1 a)2k+1 = −a.
Дійсно, |
( |
2k+1 |
a |
)2k+1 |
= |
( |
)2k+1 i(2k+1 |
a |
)2k+1 |
= −a, а це й означає, що |
|
− |
|
|
−1 |
|
|||||
2k+1 −a = −2k+1 a. |
|
|
|
|
|
|
||||
Наприклад, 3 −27 = −3 27 = −3; 5 −32 = −5 32 = −2. |
||||||||||
Зазначимо також, що значення |
|
2k+ 1 a має той самий знак, що |
||||||||
й число a, оскільки при піднесенні до непарного степеня знак числа не
змінюється. |
|
|
|||
Також за означенням кореня п-го степеня |
можна записати, що |
||||
в тому випадку, коли існує значення n a, виконується рівність |
|||||
|
|
|
|
|
|
|
(n a)n = a |
і, зокрема, при a l 0 |
( |
a)2 = a |
. |
1Усі властивості виразів виду n a наведено для випадку n Ý N, n l 2. При
п= 1 домовимося вважати, що n a = 1 a = a.
§ 9. Корінь n-го степеня та його властивості. Функція y = n x та її графік 167
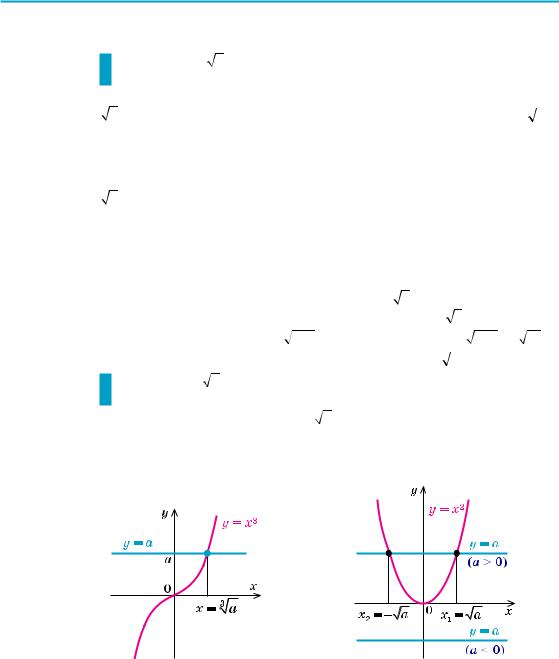
Нехай a = x, тоді за означенням квадатного кореня x2 = a і значен-
ня a буде існувати, якщо рівняння x2 = a матиме розв’язок. Зобразив и графіки функцій y = x2 і y = a (рис. 79), бачимо, що пряма y = a перетинає графік функції y = x2 тільки при a l 0 (при-
чому при a > 0 — у двох точках: x1 = a і x2 = − a, а при a = 0 — тільки в одній точці x = 0). Отже, при будь-яких значеннях
a l 0 існує значення a, оскільки функція y = x2 набуває всіх значень із проміжку [0; +∞).
Розглянемо розв’язки рівняння xn = a для парних значень n = 2k (k N).
Рівняння x2 = a при a < 0 не має коренів, оскільки квадрат будьякого числа не може бути від’ємним (на рисунку 79 пряма у = а при a < 0 не перетинає графік функції у = х2). Так само рівняння x2k = a (k N) при a < 0 не має коренів (оскільки парний степінь будь-якого числа не може бути від’ємним).
При a = 0 рівняння x2k = 0 (k N) має єдиний корінь x = 0 (оскільки парний степінь будь-якого відмінного від нуля числа — число додатне, тобто не рівне нулю, а 02k = 0).
При a > 0 за означенням кореня 2k-го степеня (2k a)2k = a. Отже, x =2k a —коріньрівнянняx2k = a.Але (−2k a)2k =(2k a)2k = a, тому x = −2k a —
теж корінь рівняння x2k = a. Ін их коренів це рівняння не має, оскільки властивості функції y = x2k аналогічні властивостям функції y = x2: при x l 0 функція зростає, отже, значення a вона може набувати тільки при
одному значенні аргументу (x =2k a). Аналогічно при x m 0 функція y = x2k спадає, тому значення a вона може набувати тільки при одному значенні аргументу (x = −2k a). Таким чином, рівняння x2k = a при a > 0 має тільки два корені: x = ±2k a.
|
Наприклад, рівняння x10 = –1 не має коренів, а рівняння x6 = 5 має |
||
корені x = ±6 5. |
|||
3. |
Властивості кореня п-го степеня можна обґрунтувати, спираючись |
||
на означення кореня n-го степеня. |
|||
|
|
|
|
1) |
Формула |
2k+1 −a = −2k+1 a |
була обґрунтована в пункті 1 пояснень. |
|
Обґрунтуємо ін і формули, наведені в таблиці 18. |
||
Нагадаємо, що за означенням кореня п-го степеня для доведення
рівності n A = B (при A l 0, B l 0) достатньо перевірити рівність
Вn = А.
.
§ 9. Корінь n-го степеня та його властивості. Функція y = n x та її графік 169
За допомогою формули n ab = n an b (а l 0, b l 0) можна одержати важливі наслідки: формули винесення множника з-під знака кореня або внесення множника під знак кореня.
Дійсно, при а l 0, b l 0 n anb = n an i n b = an b. Розглядаючи одержа-
ну формулу зліва направо, маємо формулу винесення невід’ємного множ ника зпід знака кореня:
n anb = an b ,
а справа наліво — формулу внесення невід’ємного множника під знак кореня:
an b = n anb .
Наприклад, 5 96 = 5 32 i 3 = 5 25 i 3 = 25 3.
8)Зазначимо ще одну властивість коренів n-го степеня:
для будьяких невід’ємних чисел a і b
якщо a > b, то n a > n b .
Доведемо це методом від супротивного. Припустимо, що n a m n b.
Тоді при піднесенні обох частин останньої нерівності з невід’ємними
членами до n-го степеня (із збереженням знака нерівності) одержуємо правильну нерівність a m b. Це суперечить умові a > b. Отже, на е припущення неправильне і n a > n b.
Наприклад, ураховуючи, що 21 > 16, одержуємо 4 21 > 4 16. Оскільки 4 16 = 2, маємо, що 4 21 > 2.
Узагальнення властивостей кореня n-го степеня1
Основна частина формул, які виражають властивості коренів n-го степеня, обґрунтована для невід’ємних значень підкореневих виразів. Але інколи доводиться виконувати перетворення виразів з коренями n-го степеня і в тому випадку, коли таких обмежень немає, наприклад добувати корінь квадратний (або в загальному випадку корінь парного
степеня) з добутку ab від’ємних чисел (a < 0, b < 0). Тоді ab > 0 і 2k ab існує, проте формулою
n ab = n an b |
(1) |
скористатися не можна: вона обґрунтована тільки для невід’ємних значень a і b. Але у випадку ab > 0 маємо: ab = | ab | = | a |•| b | і тепер | a | > 0 та | b | > 0. Отже, для добування кореня з добутку | a |•| b | можна використати формулу (1).
1 Цей матеріал є обов’язковим тільки для класів фізико-математичного профілю.
