
+_Algebra10_Nelin_profil
.pdf
§ 9. Корінь n-го степеня та його властивості. Функція y = n x та її графік 181
12*. Винесіть множник за знак кореня:
|
1) |
|
4 a4b14 ; |
2) 7 a9b8 ; |
3) 6 64a12b7 ; |
|
4) 8 a17b9 . |
|||||||||||||||||||
13. |
Внесіть множник під знак кореня (a > 0, b > 0): |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1) |
a3 7; |
|
|
|
|
2) −b4 ab; |
3) ab7 5; |
|
|
|
4) ab2 6 |
a |
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14*. Внесіть множник під знак кореня: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1) |
a4 7; |
|
|
|
|
2) a3 7 ab; |
3) ab6 |
2b |
; |
|
|
|
4) −b8 −3b3 . |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15. |
Спростіть вираз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1) |
|
8 a8 при a < 0; |
2) 5 a5 |
при a < 0; |
|
|
|
|
|
|
|
|
|||||||||||||
|
3) |
|
4 a4 − 3 a3 |
при a > 0; |
4) 7 a7 + 6 a6 |
при a < 0. |
|
|
|
|
||||||||||||||||
16*. Спростіть вираз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1) |
|
4 2ab3 i4 16a3b5 ; |
2) 6 ab3c i 6 a5b4c i 6 b5c4 ; |
|
|
|
|
||||||||||||||||||
|
3) |
|
8 a6 5 a4 ; |
|
|
4) 4 a3 3a5 2a2 . |
|
|
|
|
|
|
|
|
||||||||||||
17. |
Спростіть вираз: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1) |
|
|
a − b |
|
|
|
− 3 ab; |
|
|
|
|
2) |
|
|
x − y |
− |
|
x + 4 xy |
; |
||||||
|
|
|
3 a − 3 |
b |
|
|
|
|
|
|
|
|
4 x − 4 y |
4 x + 4 y |
||||||||||||
|
3*) |
|
|
3 ab2 −26 ab5 + b |
, де a > 0, b > 0, a ≠ b; |
|
|
4*) |
|
|
3 x − 6 xy |
. |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
3 a2b − ab |
|
|
|
|
|
|
|
3 y − 6 xy |
|
|
|
|
||||||||||
18°. Розв’яжіть рівняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1) x3 = 7; |
|
2) x6 = 3; |
|
|
|
|
3) x5 = –5; |
|
|
|
|
||||||||||||||
|
4) x8 = –13; |
|
5) x4 = 16; |
|
|
|
6) x3 = –64. |
|
|
|
|
|||||||||||||||
19. Побудуйте графік функції: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1°) y = 4 x; |
2°) y = 5 x; |
3°) y = 7 x; |
|
|
|
4°) y = 6 x; |
|||||||||||||||||||
|
5) |
y = 3 |
|
x |
|
; |
6) y = −3 x; |
7) y = 4 −x. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
20. Розв’яжіть графічно рівняння: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1) |
|
3 x =2−x; |
|
2) x =6−x; |
3) 3 x−2 =4−x; |
|
4) −x = x+2. |
||||||||||||||||||
Перевірте підстановкою, що значення x дійсно є коренем рівняння.
21*. Доведіть, що рівняння, наведені в завданні 20, не мають ін их коренів, крім знайдених графічно.

182 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ |
|
|
9.3. Обернена функція |
|
|
|
Таблиця 20 |
|
1. Поняття оберненої функції |
|
|
Якщо функція y = f (x) набуває кожного свого значення в єдиній точці її |
||
області визначення, то можна задати функцію y = g (x), яка називається |
||
оберненою до функції y = f (x): |
|
|
для кожного a D (f), |
|
|
якщо f (a) = b, то g (b) = a |
||
E (f) = D (g); D (f) = E (g) |
||
Функції f (x) і g (x) взаємно обернені |
|
|
2. Властивості оберненої функції |
|
|
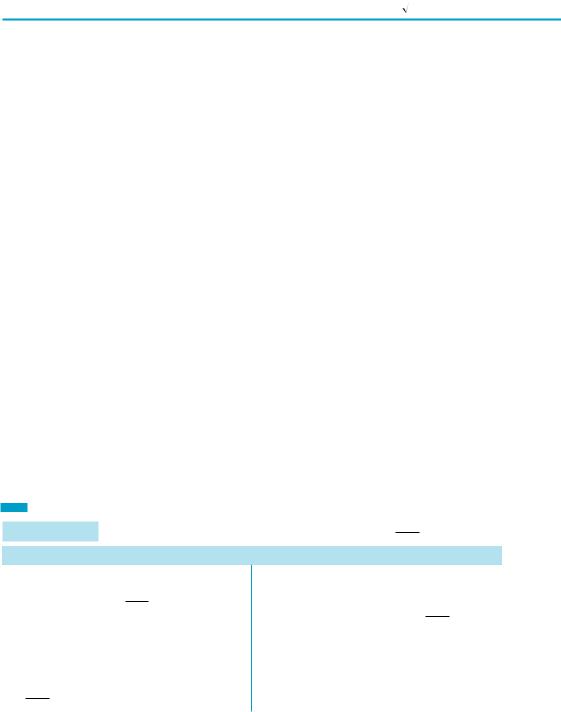
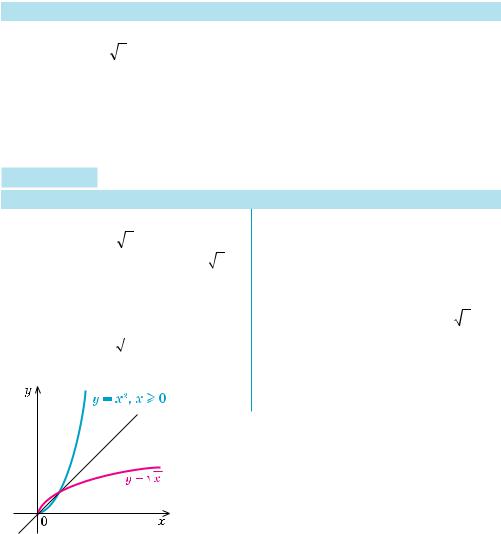
1) Графіки прямої та оберненої |
||
функцій |
симетричні |
відносно |
прямої y = x |
|
|
2) Якщо функція f (x) зростає (спа- |
||
дає) на деякому проміжку, то вона |
||
має обернену функцію на цьому |
||
проміжку, яка зростає, якщо f (x) |
||
зростає, і спадає, якщо f (x) спа- |
||
дає |
|
|

§ 9. Корінь n-го степеня та його властивості. Функція y = n x та її графік 183
Продовження табл. 20
3. Практичний спосіб знаходження формули функції, оберненої до функції y = f (x)
|
Алгоритм |
|
|
|
Приклад |
|
|
|
|
|
|||||
1. З’ясувати, чи буде |
функція |
Знайдіть функцію, обернену до |
|||||
y = f (x) оборотною на всій об- |
функції y = 2x + 4. |
|
|||||
ласті |
визначення: |
для цього |
|
З рівності y = 2x + 4 можна |
|||
достатньо з’ясувати, чи має рів- |
однозначно виразити x через y: |
||||||
няння y = f (x) єдиний корінь |
|
|
1 |
|
|||
відносно змінної x. |
|
|
|
x = |
2 y−2. |
|
|
Якщо ні, то виділити (якщо мож- |
Ця формула |
задає |
обернену |
||||
ливо) проміжок, де існує оберне- |
функцію, але в ній аргумент позна- |
||||||
на функція (наприклад, це може |
чено через y, а функцію — через x. |
||||||
бути |
проміжок, |
де |
функція |
Позначимо в одержаній фор- |
|||
y = f (x) зростає або спадає). |
мулі |
аргумент через x, |
а функ- |
||||
2.З рівності y = f (x) виразити x цію — через y.
через y. |
|
1 |
3. В одержаній формулі ввести |
Маємо функцію y = |
2x−2, обер- |
традиційні позначення — аргу- |
нену до функції y = 2x + 4. |
|
мент позначити через x, а функ- |
|
|
цію — через y. |
|
|
Пояснення й обґрунтування
1. Поняття оберненої функції. Відомо, що залежність ляху від часу для тіла, яке рухається рівномірно з постійною видкістю v0, виражається формулою S = v0t. З цієї формули можна знайти обернену залеж-
ність — часу від пройденого ляху t = S . Функцію t(S) = S називають |
|
v0 |
v0 |
оберненою до функції S (t) = v0t. Зазначимо, що в розглянутому прикладі кожному значенню t (t l 0) відповідає єдине значення S і, навпаки, кожному значенню S (S l 0) відповідає єдине значення t.
Розглянемо процедуру одержання оберненої функції в загальному вигляді.
Нехай функція f (x) набуває кожного свого значення в єдиній точці її області визначення (така функція називається оборотною). Тоді для кожного числа у0 = b (з області значень функції f (x)) існує єдине значення х0 = a, таке, що f (a) = b. Розглянемо нову функцію g (x), яка кожному числу b з області значень функції f (x) ставить у відповідність число a, тобто g (b) = a для кожного b з області значень функції f (x).
Уцьому випадку функція g (x) називається оберненою до функції f (x),
афункція f (x) — оберненою до функції g (x).
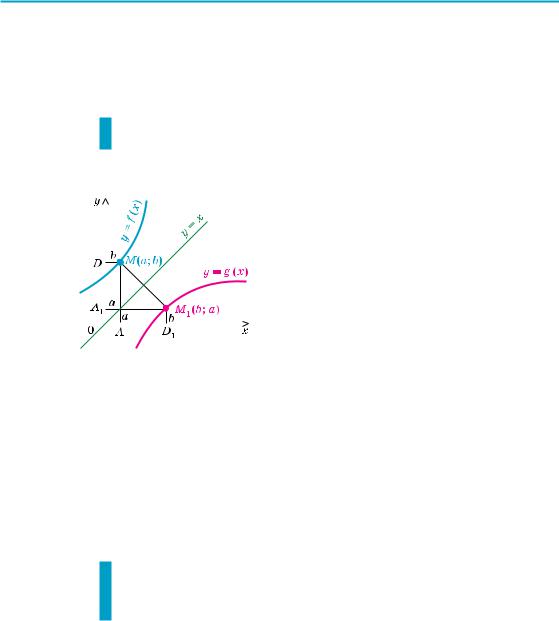
186 |
Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
обернену функцію, але в ній аргумент |
|
|
|
|
|
|
|
|
|
|
|
позначено через y, а функцію — че- |
|
|
|
|
|
рез x. Змінюючи позначення на |
|
|
|
|
|
традиційні, одержуємо кінцевий ре- |
|
|
|
|
|
зультат. |
|
|
|
Знайдіть функцію, обернену до функції y = х2. |
||
|
Приклад 2. |
||||
|
|
Розв’язання |
|
Коментар |
|
|
|
|
|||
|
|
З рівності y = х2 при y l 0 |
Область значень заданої функ- |
||
|
одержуємо x = ± y. Тоді при y > 0 |
ції: y l 0. Але при y > 0 з рівності |
|||
|
y = x2 не можна однозначно вирази- |
||||
|
одному значенню y відповідають два |
||||
|
ти x через y. Наприклад, при y = 4 |
||||
|
значення x. Отже, на всій |
області |
|||
|
одержуємо x = ±2. Через це ми не |
||||
|
визначення x (–∞; +∞) |
функція |
|||
|
можемо значенню y = 4 поставити |
||||
|
y = x2 не є оборотною, і для неї не- |
||||
|
можливо знайти обернену функцію. |
у відповідність єдине число, щоб по- |
|||
|
будувати обернену функцію. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приклад 3. |
Знайдіть функцію, обернену до функції y = х2 при x l 0. |
||||||||||
|
Розв’язання |
|
|
|
|
Коментар |
|
||||
|
З рівності y = х2 |
при y l 0 |
|
Множина значень заданої функ- |
|||||||
одержуємо |
x = ± y. |
Ураховуючи, |
ції: y l 0. При x l 0 задана функція |
||||||||
y |
= х2 зростає, отже, на |
проміжку |
|||||||||
що за умовою x l 0, маємо x = |
y. |
||||||||||
x |
l 0 вона має обернену функцію. |
||||||||||
|
Позначимо аргумент через |
x, |
|||||||||
|
Тому на цьому проміжку рівняння |
||||||||||
а |
функцію — через y |
і |
одержимо, |
||||||||
х2 = y ми зможемо однозначно роз- |
|||||||||||
що функцією, оберненою до функції |
в’язати: при x l 0 маємо x = y. |
||||||||||
y = х2, яка задана тільки при x l 0, |
|||||||||||
|
Ця |
формула |
задає |
обернену |
|||||||
буде функція y = x. |
|
|
|
|
|||||||
|
|
|
функцію, але в ній аргумент позна- |
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
чено через y, а функцію — через x. |
|||||
|
|
|
|
|
|
Замінюючи позначення на традицій- |
|||||
|
|
|
|
|
|
ні, одержуємо кінцевий результат. |
|||||
|
|
|
|
Зауваження. У прикладах 2 і 3 ми фак- |
|||||||
|
|
|
|
тично розглядаємо різні функції (вони мають |
|||||||
|
|
|
|
різні області визначення), хоча в обох випад- |
|||||||
|
|
|
|
ках ці функції задаються однією й тією самою |
|||||||
|
|
|
|
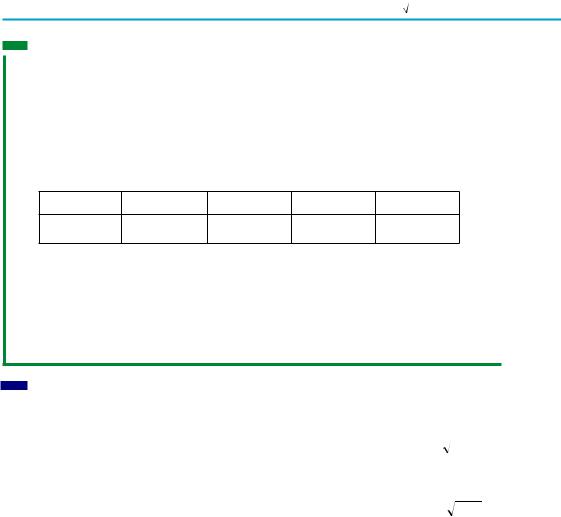
формулою. Як відомо, графіком функції y = х2 |
|||||||
|
|
|
|
(приклад 2) є парабола, а графіком функції |
|||||||
|
|
|
|
y = х2 при x l 0 (приклад 3) є тільки права |
|||||||
|
Рис. 85 |
|
вітка цієї параболи (рис. 85). |
|
|
||||||
§ 9. Корінь n-го степеня та його властивості. Функція y = n x та її графік 187
Запитання для контролю
1.За якої умови для заданої функції y = f (x) можна побудувати обернену функцію?
2.Поясніть побудову графіка оберненої функції на прикладі функції y = f (x), яка задана таблицею:
x |
0 |
2 |
4 |
6 |
|
|
|
|
|
f (x) |
1 |
3 |
5 |
7 |
|
|
|
|
|
Задайте обернену функцію y = g (x) за допомогою таблиці:
x
g(x)
3.Як розміщено графіки прямої і оберненої функцій, якщо їх побудовано в одній системі координат? Проілюструйте відповідну властивість графіків на прикладі.
4.Обґрунтуйте взаємне розміщення графіків прямої і оберненої функцій.
5.Чи існує функція, обернена до функції y = x2, де x m 0? Поясніть це,
спираючись на відповідні властивості оберненої функції. Якщо обернена функція існує, то задайте її формулою виду y = g (x).
Вправи
1.Запи іть формулу, яка задає функцію y = g (x), обернену до заданої. Укажіть область визначення і множину значень функції g (x):
1°) y = 3x – 6; 2°) y = –3x – 6; 3) y = 2 |
; |
4) y = −1 |
; 5) y = x. |
x |
|
x |
|
2.На одному рисунку побудуйте графік даної функції і функції, оберненої до даної:
1°) y = 2x; |
2°) y = x – 2; 3) y = −x1; 4*) y = |
|
1 |
; 5*) y = x+1. |
x |
−1 |
3.Знайдіть функцію, обернену до даної на заданому проміжку, і побудуйте на одному рисунку графік даної функції і функції, оберненої до неї:
1) y = 1 x2 |
при x l 0; |
2) y = 1 x2 |
при x m 0; |
4 |
|
4 |
|
3) y = (x – 2)2 при x l 2; |
4) y = x2 – 2 при x m 0. |
||
188 Розділ 2. СТЕПЕНЕВА ФУНКЦІЯ
§ 10 ІРРАЦІОНАЛЬНІ РІВНЯННЯ
10.1. Найпростіші способи розв’язування ірраціональних рівнянь
Таблиця 21
Поняття ірраціонального рівняння
Рівняння, у яких змінна міститься під знаком кореня, називають ірраці ональними. Для того щоб розв’язати задане ірраціональне рівняння, його найчасті е зводять до раціонального рівняння за допомогою деяких перетворень.
Розв’язування ірраціональних рівнянь
1. За допомогою піднесення обох частин рівняння до одного степеня
При піднесенні обох частин рівнян- |
При піднесенні обох частин рівняння |
||||||
ня до непарного степеня одержуємо |
до парного степеня можуть з’явитися |
||||||
рівняння, рівносильне заданому (на |
сторонні корені, які відсіюють пере- |
||||||
його ОДЗ) |
віркою |
|
|
|
|
|
|
|
|
|
|
|
|
||
Приклад 1 |
|
Приклад 2 |
|
|
|
||
Розв’яжіть рівняння 3 x−1 =2. |
Розв’яжіть рівняння |
2x+3 = x. |
|||||
(3 x−1)3 =23, |
( 2x+3)2 = x2, |
|
|
|
|||
х – 1 = 8, |
х2 – 2х – 3 = 0, х |
= –1, х |
2 |
= 3. |
|||
х = 9. |
Перевірка. |
При |
1 |
|
|
маємо: |
|
х = –1 |
|
|
|||||
Відповідь: 9. |
1 = −1 — неправильна |
рівність, |
|||||
|
отже, х = –1 — сторонній корінь. |
||||||
|
При х = 3 маємо: |
9 =3 — правиль- |
|||||
|
на рівність, |
отже, |
х = 3 — корінь |
||||
|
заданого рівняння. |
|
|
|
|
|
|
|
Відповідь: 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. За допомогою заміни змінних |
|
|
|
|
|
||
Якщо до рівняння змінна входить в одному і тому самому вигляді, то зручно відповідний вираз із змінною позначити однією буквою (новою змінною)
Приклад 3
Розв’яжіть рівняння 3 x2 + 3 x =2.
Позначимо 3 x =t. Тоді 3 x2 =(3 x)2 =t2.
Одержуємо рівняння: t2 + t = 2, t2 + t – 2 = 0, t1 = 1, t2 = –2.
Виконуємо обернену заміну: 3 x =1, тоді х = 1 або 3 x = −2, звідси х = –8.
Відповідь: 1; –8.
§ 10. Ірраціональні рівняння 189
Пояснення й обґрунтування
Ірраціональними рівняннями називають такі рівняння, у яких змінна міститься під знаком кореня. Наприклад, x−2 =5, 3 x +x =2 — ірраціональні рівняння.
Найчасті е розв’язування ірраціональних рівнянь ґрунтується на зведенні заданого рівняння за допомогою деяких перетворень до раціонального рівняння. Як правило, цього досягають піднесенням обох частин ірраціонального рівняння до одного й того самого степеня (часто декілька разів).
Слід ураховувати, що
при піднесенні обох частин рівняння до непарного степеня завжди одержуємо рівняння, рівносильне заданому (на його ОДЗ).
Наприклад, рівняння |
3 x+7 =3 |
(1) |
|
рівносильне рівнянню |
(3 |
x+7)3 =33, |
(2) |
тобто рівнянню х + 7 = 27. |
Звідси х = 20. |
|
|
Для того щоб обґрунтувати рівносильність рівнянь (1) і (2), достатньо звернути увагу на те, що рівності А = В і А3 = В3 можуть бути пра-
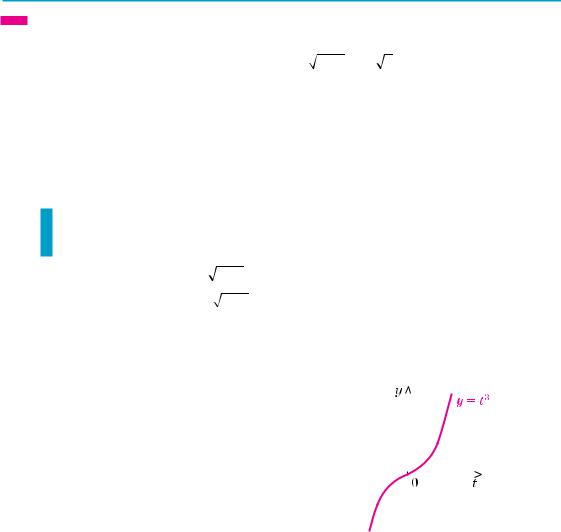
вильними |
тільки одночасно, оскільки функція |
|
|
у = t3 є зростаючою (на рисунку 86 наведено її |
|
|
|
|
|
||
графік) і кожного свого значення набуває тіль- |
|
|
|
ки при одному значенні аргументу t. Отже, усі |
|
|
|
корені рівняння (1) (які перетворюють це рів- |
|
|
|
няння на правильну рівність) будуть і коренями |
|
|
|
рівняння (2), і навпаки, усі корені рівняння (2) |
|
|
|
|
|
||
будуть коренями рівняння (1). А це й означає, |
|
|
|
що рівняння (1) і (2) є рівносильними. Аналогіч- |
|
|
|
но можна обґрунтувати рівносильність відповід- |
|
|
|
них рівнянь і у випадку піднесення обох частин |
|
|
|
|
|
||
рівняння до одного й того самого довільного не- |
Рис. 86 |
||
парного степеня. |
|
|
|
Якщо |
для розв’язування ірраціонального |
|
|
рівняння обидві частини піднести до парного степеня, то одержуємо рівняння-наслідок — коли всі корені пер ого рівняння будуть коренями другого, але друге рівняння може мати корені, що не задовольняють заданому рівнянню. Такі корені називають сторонніми для заданого рівняння. Щоб з’ясувати, чи є одержані числа коренями заданого рівнян-
ня, виконують перевірку цих розв’язків.

