
+_Algebra10_Nelin_profil
.pdf
§ 8. Многочлени від однієї змінної та дії над ними 141
Доведемо, що задане твердження виконується й при n = k + 1. Нехай
f (x) = а |
k + 1 |
хk + 1 + а |
хk |
+ … + а |
х + а |
0 |
≡ 0. |
(3) |
||||||
|
|
|
k |
|
|
|
1 |
|
|
|
|
|||
Оскільки рівність (3) виконується при всіх значеннях х, то, підстав- |
||||||||||||||
ляючи в цю рівність х = 0, одержуємо, що а0 |
= 0. Тоді рівність (3) |
|||||||||||||
перетворюється на таку рівність: а |
k + 1 |
хk + 1 |
+ а |
хk + ... + а |
х ≡ 0. Ви- |
|||||||||
|
|
|
|
|
|
|
|
|
|
k |
|
1 |
|
|
несемо х у лівій частині цієї рівності за дужки та одержимо |
||||||||||||||
х (а |
k + 1 |
хk + а |
хk – 1 |
+ ... + а |
1 |
) ≡ 0. |
|
(4) |
||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|||
Рівність (4) повинна виконуватися при всіх значеннях х. Для того
щоб вона виконувалася при х ≠ 0, повинна виконуватися тотожність
аk + 1хk + аkхk – 1 + ... + а1 ≡ 0.
У лівій частині цієї тотожності стоїть многочлен із степенями змінної від х0 до хk. Тоді за припущенням індукції всі його коефіцієнти дорівнюють нулю: аk + 1 = ak = … = а1 = 0. Але ми довели також, що а0 = 0, тому наше твердження виконується і при п = k + 1. Отже, твердження теореми справедливе для будь-якого цілого невід’ємного п, тобто для всіх многочленів.
Многочлен, у якого всі коефіцієнти рівні нулю, зазвичай називають
нульовим многочленом, або нуль-многочленом, і позначають 0 (х) або просто 0 (оскільки 0 (х) = 0).
Теорема 3. Якщо два многочлени f (x) і g (x) тотожно рівні,
то вони збігаються (тобто їхні степені однакові й коефіцієнти при однакових степенях рівні).
Нехай многочлен |
|
|
f (х) = а |
хn |
+ а |
n – 1 |
хn – 1 |
+ ... + а |
х2 |
+ а |
х + а |
0 |
, |
|||||||||||
а многочлен g (x) = b |
|
xm + b |
|
|
|
n |
|
|
|
|
|
|
х2 + b |
2 |
|
1 |
|
|
||||||
m |
m – 1 |
xm – 1 |
+ ... + b |
x + b |
. Розгляне- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
0 |
|
|
|
||||
мо многочлен f (x) – g (x). Оскільки многочлени f (x) і g |
(x) за умо- |
|||||||||||||||||||||||
вою тотожно рівні, то многочлен f (x) – g (x) тотожно дорівнює 0. |
||||||||||||||||||||||||
Отже, усі його коефіцієнти дорівнюють нулю. |
|
|
|
|
|
|
|
|||||||||||||||||
Але f (x) – g (x) = (a – b |
) + (a |
1 |
– b |
) x + (а |
2 |
– b |
) х2 |
+ ... . |
|
|
|
|||||||||||||
0 |
|
0 |
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
Тоді a0 – b0 = 0, a1 – b1 |
= |
0, а2 |
|
– b2 |
= 0, ... . |
|
Звідси a0 = b0, a1 = b1, |
|||||||||||||||||
а2 = b2, ... . Як бачимо, якщо припустити, що в якогось із двох заданих многочленів степінь вищий, ніж у другого многочлена (наприклад, п більше т), то коефіцієнти різниці дорівнюватимуть нулю. Тому,
починаючи з (т + 1)-го номера, усі коефіцієнти aі також дорівнюватимуть нулю. Отже, многочлени f (x) і g (x) дійсно мають однаковий степінь і відповідно рівні коефіцієнти при однакових степенях. Теорема 3 є основою так званого методу невизначених коефіцієнтів.
Покажемо його застосування на такому прикладі.
Приклад. Доведіть, що (х + 2) (х + 4) (х + 6) (х + 8) + 16 є повним квадратом.
Заданий многочлен є многочленом четвертого степеня, тому він може бути повним квадратом тільки многочлена другого степеня.


§ 8. Многочлени від однієї змінної та дії над ними 143
8.2.Дії над многочленами. Ділення многочлена на многочлен
зостачею
Додавання і множення многочленів від однієї змінної виконують за допомогою відомих правил додавання і множення многочленів. У результаті виконання дій додавання або множення над многочленами від однієї змінної завжди одержують многочлен від тієї самої змінної.
З означення добутку двох многочленів випливає, що старший член добутку двох многочленів дорівнює добутку старших членів множників, а вільний член добутку дорівнює добутку вільних членів множників. Звідси одержуємо, що степінь добутку двох многочленів дорівнює сумі степенів множників.
При додаванні многочленів одного степеня одержують многочлен цього самого степеня, хоча іноді можна одержати многочлен меншого степеня.
Наприклад, 2х3 – 5х2 + 3х + 1 + (–2х3 + 5х2 + х + 5) = 4х + 6.
При додаванні многочленів різних степенів завжди одержуємо многочлен, степінь якого дорівнює більшому степеню доданку.
Наприклад, (3х3 – 5х + 7) + (х2 + 2х + 1) = 3х3 + х2 – 3х + 8.
Ділення многочлена на многочлен означається аналогічно діленню цілих чисел. Нагадаємо, що ціле число а ділиться на ціле число b (b ≠ 0), якщо існує таке ціле число q, що а = b•q.
Означення. Многочлен А (х) ділиться на многочлен В (х) (де
В (х) — ненульовий многочлен), якщо існує такий многочлен Q (x), що
А (х) = В (х)•Q (x).
Як і для цілих чисел, операція ділення многочлена на многочлен виконується не завжди, тому в множині многочленів уводять операцію
ділення з остачею. Кажуть, що
многочлен А (х) ділиться на многочлен В (х) (де В (х) — ненульовий многочлен) з остачею, якщо існує така пара многочленів Q (x) і R (x), що А (х) = В (х)•Q (x) + R (x), причому степінь остачі R (x)
менший за степінь дільника В (х). (Зазначимо, що в цьому випадку многочлен Q (х) називається неповною часткою.)
Наприклад, оскільки х3 – 5х + 2 = (х2 – 5) х + 2, то при діленні многочлена х3 – 5х + 2 на многочлен х2 – 5 одержуємо неповну частку х і остачу 2.
Іноді ділення многочлена на многочлен, як і ділення багатозначних чисел, зручно виконувати «куточком», користуючись таким алгоритмом.
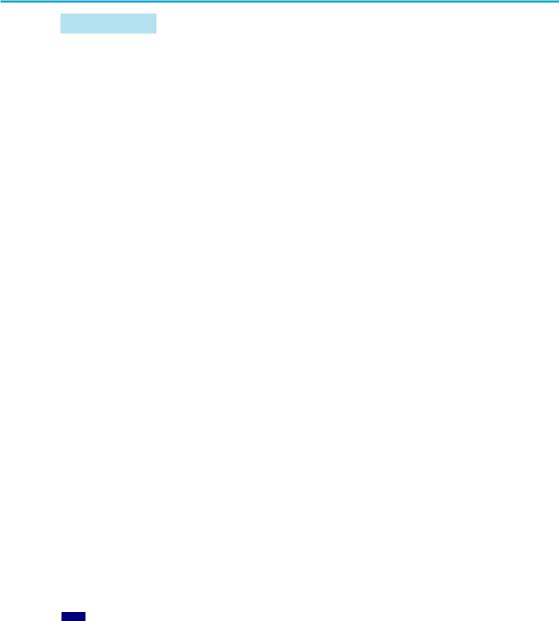

§ 8. Многочлени від однієї змінної та дії над ними 145
2.Виконайте ділення многочлена на многочлен з остачею:
1)4х4 – 2х3 + х2 – х + 1 на x2 + x + 2;
2)х5 + х4 + х3 + х2 + 1 на х2 – х – 2.
3.При яких значеннях а і b многочлен А (х) ділиться без остачі на многочлен В (х)?
1)А (х) = х3 + ах + b, В (х) = х2 + 5х + 7;
2)А (х) = 2х3 – 5х2 + ах + b, В (х) = х2 – 4;
3)А (х) = х4 – х3 + х2 – ах + b, В (х) = х2 – х + 2.
4.Знайдіть неповну частку і остачу при діленні многочлена А (х) на многочлен В (х) методом невизначених коефіцієнтів:
1)А (х) = х3 + 6х2 + 11х + 6, В (х) = х2 – 1;
2)А (х) = х3 – 19х – 30, В (х) = х2 + 1.
8.3. теорема Безу. Корені многочлена. Формули Вієта
Розглянемо ділення многочлена f (x) на двочлен (х – а). Оскільки степінь дільника дорівнює 1, то степінь остачі, яку ми одержимо, повинен бути меншим за 1, тобто в цьому випадку остачею буде деяке число R. Таким чином, якщо розділити многочлен f (x) на двочлен (х – а), то одержимо
f (x) = (х – а)•Q (x) + R.
Ця рівність виконується тотожно, тобто при будь-якому значенні х. При х = а маємо: f (а) = R. Одержаний результат називають теоремою Безу1.
Теорема 1 (теорема Безу). Остача від ділення многочлена f (х)
на двочлен (х – а) дорівнює f (а) (тобто значенню многочлена при х = а).
Приклад 1. Доведіть, що х5 – 3х4 + 2х3 + 4х – 4 ділиться без остачі на
х– 1.
Підставивши в f (х) = х5 – 3х4 + 2х3 + 4х – 4 замість х значення 1, одержуємо: f (1) = 0. Отже, остача від ділення f (х) на (х – 1) дорівнює 0, тобто f (x) ділиться на (х – 1) без остачі.
Означення. Число α називається коренем многочлена f (x), якщо
f (α) = 0.
Якщо многочлен f (х) ділиться на (х – α), то α — корінь цього многочлена.
Дійсно, якщо f (х) ділиться на (х – α), то f (х) = (х – α) • Q (x) і тому f (α) = (α – α) • Q (α) = 0. Отже, α — корінь многочлена f (х).
1Безу Етьєн (1730–1783), французький математик, який зробив значний внесок у розвиток теорії алгебраїчних рівнянь.



§ 8. Многочлени від однієї змінної та дії над ними 149
5. Остача |
від ділення многочлена f (x) на |
3х2 – 5х + 2 |
дорівнює |
7х + 1. |
Знайдіть остачу від ділення цього |
многочлена на |
двочлени |
х – 1 і 3х – 2.
6.Запишіть формули Вієта при п = 4.
7.Складіть кубічний многочлен, який має корені 5, –2, 1 і коефіцієнт при старшому члені –2. Розв’яжіть задачу двома способами.
8. При яких значеннях а сума квадратів коренів тричлена х2 –
–(а + 2) х + 3а дорівнює 12?
9.Яку кратність має корінь 2 для многочлена f (х) = х5 – 5х4 + 7х3 –
–2х2 + 4х – 8?
10.Складіть кубічний многочлен, який має корінь 3 кратності 2 і корінь (–1), а коефіцієнт при старшому члені 2.
11.Знайдіть такі а і b, щоб число 3 було коренем не менш ніж другої кратності для многочлена f (х) = х3 – 5х2 + ах + b.
12.Складіть квадратне рівняння, корені якого протилежні кореням рівняння х2 – 5х + 1 = 0.
13.Складіть квадратне рівняння, корені якого обернені до коренів рівняння 2х2 – 5х + 1 = 0.
14.Складіть квадратне рівняння, коренями якого є квадрати коренів рівняння х2 + 6х + 3 = 0.
8.4.схема Горнера
Ділити многочлен f (x) на двочлен (х – а) іноді зручно за допомогою
спеціальної схеми, яку називають схемою Горнера. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Нехай многочлен f (x) = а хn |
+ а |
хn – 1 |
+ ... + а |
n – 1 |
х + а |
n |
(a |
0 |
≠ 0) потріб- |
||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
но розділити на двочлен (х – |
а). У результаті ділення многочлена п-го |
||||||||||||||||||||||||||||||||
степеня на многочлен першого степеня одержимо деякий многочлен |
|||||||||||||||||||||||||||||||||
Q (x) (п – 1)-го |
степеня (тобто |
|
Q (x) = b |
|
xn – 1 |
+ b |
|
xn – 2 |
+ |
|
... + b |
n – 2 |
x + |
||||||||||||||||||||
|
b0 ≠ |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
= |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
+ bn – 1, де |
0) |
і остачу |
R. Тоді f |
|
(x) |
(х – |
а)•Q (x) + R, |
тобто |
|||||||||||||||||||||||||
|
а |
хn |
+ а хn – 1 |
+ ... + а |
n – 1 |
х + а |
n |
= |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= (х |
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
) + R. |
|
|
||||||||
– а)•(b |
xn – 1 + b |
xn – 2 + ... + b |
n – 2 |
+ b |
n |
– 1 |
|
|
|||||||||||||||||||||||||
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Оскільки ліва і права частини тотожно рівні, то перемножимо мно- |
|||||||||||||||||||||||||||||||||
гочлени, які стоять справа, і прирівняємо коефіцієнти при відповід- |
|||||||||||||||||||||||||||||||||
них степенях х: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хn |
|
|
|
|
|
|
а |
|
|
= b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
хn – 1 |
|
|
|
|
а0 |
|
= b0 |
– аb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
хn – 2 |
|
|
|
|
а21 |
|
= b21 |
– аb10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
....... |
|
|
|
|
......................... |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
х1 |
|
|
|
|
|
|
а |
n |
– 1 |
= b |
|
|
– аb |
n – 2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
х0 |
|
|
|
|
|
|
а |
|
n – 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
= R |
– |
аb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n – 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Знайдемо із цих рівностей коефіцієнти b0, b1, ..., bn – 1 і остачу R: |
|
||||||||||||||||||||||||||||||||
b0 = а0, b1 = ab0 + a1, b2 = ab1 + a2, …, bn – 1 = abn – 2 + an – 1, |
R = abn – 1 + an. |
||||||||||||||||||||||||||||||||

