2.1.Аберація світла.

Розглянемо деякі наслідки з інваріантності рівнянь Максвела відносно перетворень Лоренца.Нехай у системі K поширюється плоска електромагнітна хвиля , що характеризується векторними полями:

(1)

При переході до системи К' вектори поля можуть змінюватись, але фаза залишається незміною, оскільки (ωt-kr) є скалярна величина, тому не залежить від системи відліку.

Якщо ввести чотиримірний вектор r_i(x,y,z,ict) то фаза може бути записана:

(2)

звідси видно , що величина k_i(k_x,k_y,k_z,iω/c) є чотири вимірний вектор; k_i називають чотиривимірним хвильовим вектором.

Запишемо формули перетворення для 4 –вектора k_i:

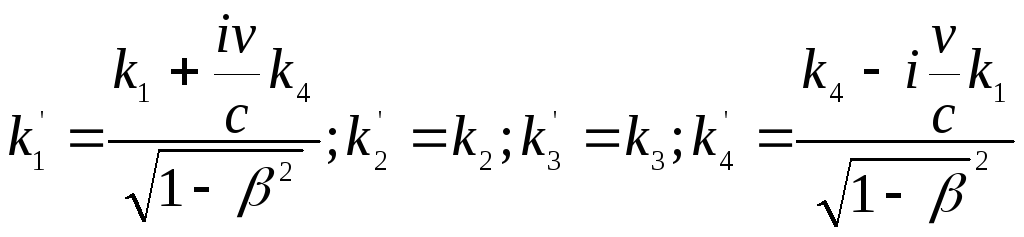(3)

Компоненти вектора k^'_i у тривимірному записі мають вигляд :

тут і далі α', β', γ'-кути між осями X', Y', Z' відносно і хвильовим вектором k'. Рівняння (3 ) тепер матимуть вигляд:

(4)

або

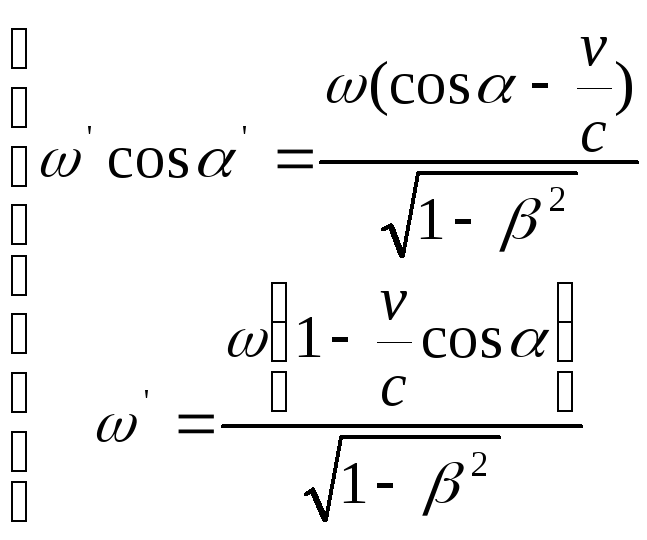(4')

Поділивши перше рівняння (4') на друге , одержимо :

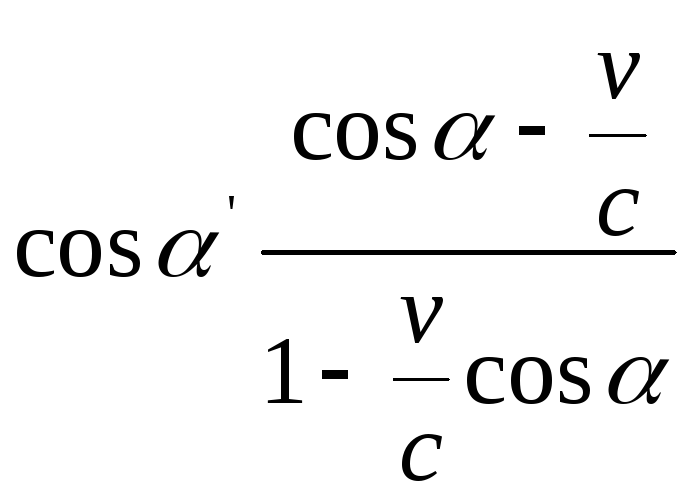(5)

З другого і третього рівнянь (3) знайдемо аналогічно :

(6)

де α, β, γ-кути між векторам k і відносно осями X, Y, Z. З цих рівнянь, підставляючи в них ω' з (4), знайдемо :

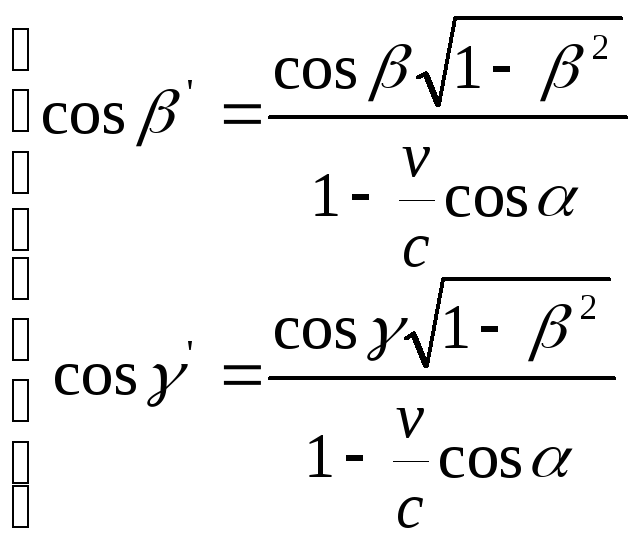(7)

З рівнянь (5) і (7) випливає існування аберації світла при спостереженні зірок .

Нехай зірка нерухома в системі K . Якщо промінь світла від неї перпендикулярний до напрямку руху Землі і лежить в площині OXY, то :cosα=0; c0sβ=1; cosγ=0

Підставляючи ці значення у формули (5) і (7), матимемо для Землі (система K'), що рухається відносно зірки з швидкістю V:

(8)

Оскільки cosγ'=0, то в системі K' промінь від зірки також лежить у площині OX'Y'. Далі матимемо:

(9)

звідки знайдемо:

(10)

Для малих v/c(v<<c) одержимо :

(10')

Тут кут β'-кут, що визначає величину аберації зірок.

2.2.Ефект Доплера.

Іншим наслідком з інваріантності рівнянь Максвела може служити ефект Доплера.

Використовуючи закон перетворення хвильвого 4-вектора легко розглянути так званий ефект Доплера, тобто зміна частоти хвилі ω, яка випромінюється джерелом, що рухається по відношенню до спостерігача в системі відліку (К), в порівнянні із власною частотою ω' того ж джерела в системі відліку (К'), в якій воно нерухоме.

Нехай v – швидкість джерела, тобто швидкість (К') відносно (К). Використаємо формули перетворення Лоренцa 4-вимірних векторів:

запишемо для к₄:

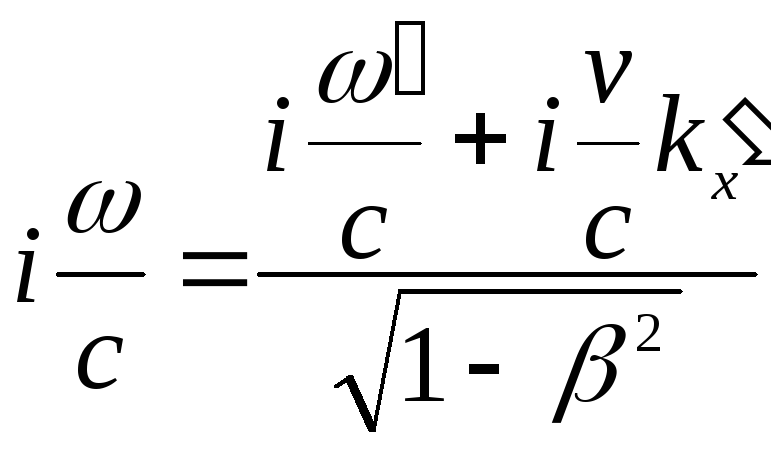
Оскільки k'_x=k'cosα', то

Можна розглянути різні випадки:

1. Система з джерелом рухається назустріч приймачеві: в цьому випадку

ω>ω' — спостерігається фіолетове зміщення.

2. Система (К') віддаляється від системи (К):

тепер ω<ω' спостерігається червоне зміщення.

3. Джерело рухається перпендикулярно до спостерігача: α'=π/2:

в цьому випадку також ω>ω'.Це так званий релятивістський ефект Айве.

3. Рівняння поля в тензорній формі

Запишемо вирази для напруженостей полів через потенціали :

(1)

Формули (1) представлені в трьохмірних позначеннях і тому незручні для вияснення закону перетворення цих величин при зміні системи відліку.

Покажемо, що компоненти напруженості полів утворюють чотирьохвимірний тензор другого рангу і це дасть можливість записати рівняння поля в тензорній формі .

Запишемо рівняння (1) у вигляді системи рівнянь для компонент:

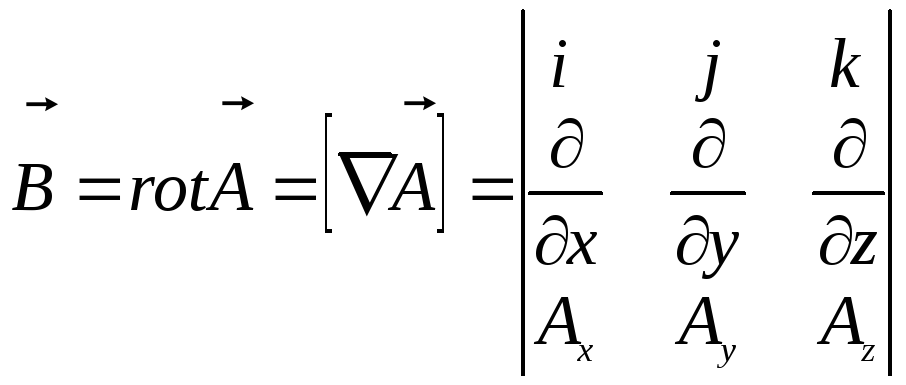
(2)

Аналогічно запишемо для напруженості електричного поля. Врахувавши, що потенціали А і φ утворюють єдиний чотиривимірний вектор:

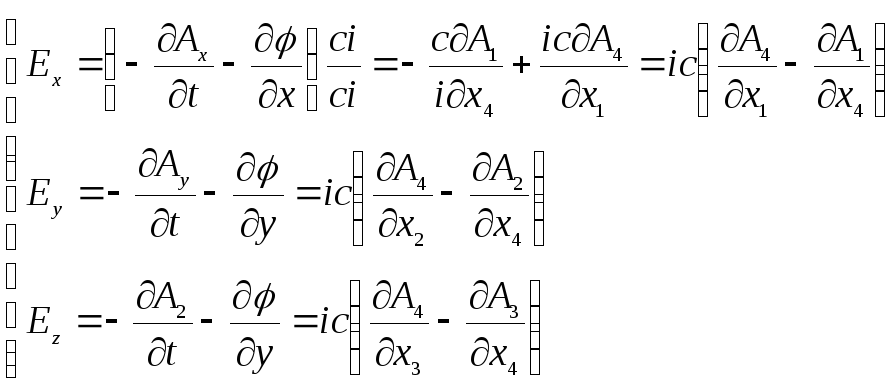(3)

Введемо антисиметричний тензор другого рангу по закону:

(4)

Компоненти напруженостей полів, згідно формул (2)-(4), можна зобразити як компоненти цього тензора:

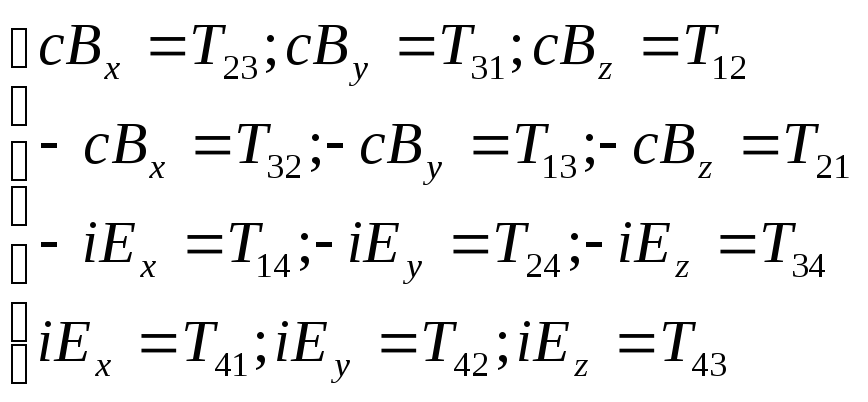
Ми одержали 16 елементів, з яких можна утворити матрицю:

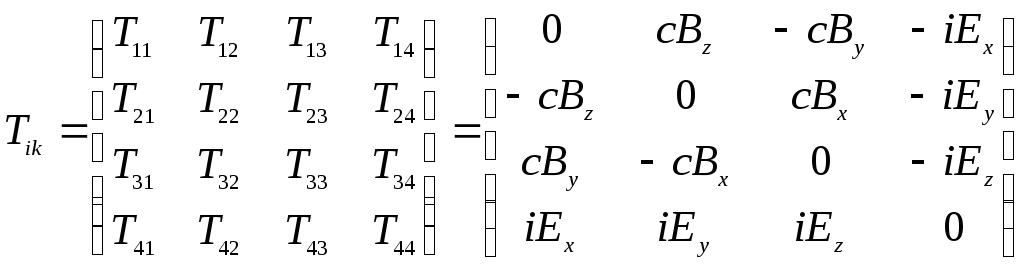(5)

Отже компоненти напруженостей полів є компонентами тензора T_ik , який називається тензором електромагнітного поля .

Ми одержали математичний запис який виражає фізичну єдність електричного і магнітного полів.

Ввівши цей тензор, можна легко записати рівняння Максвела у релятивістськоінваріантній формі.

З рівності (4) можна утворити таке рівняння:

(6)

Покажемо, що (6) представляє собою першу пару системи рівнянь Максвела в тензорній формі.

Покладемо: i=1; k=2; l=3, одержимо:

або використовуючи компоненти тензора (5):

виберемо тепер i=1; k=2; l=4, ,

або

або

тобто

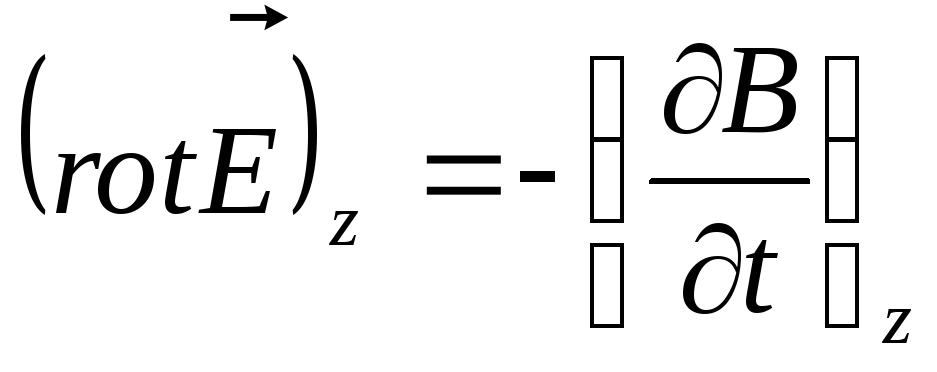
Таким чином, (6) записує першу пару рівнянь Максвела в тензорній формі.

Покажемо тепер, що рівняння

представляє другу пару системи рівнянь Максвела в тензорній формі.

Візьмемо для прикладу, і=1, тоді

або

звідси