2.Поле системи зарядів на далеких віддалях.

Загальні формули для потенціалів, що запізнюються досить складні:

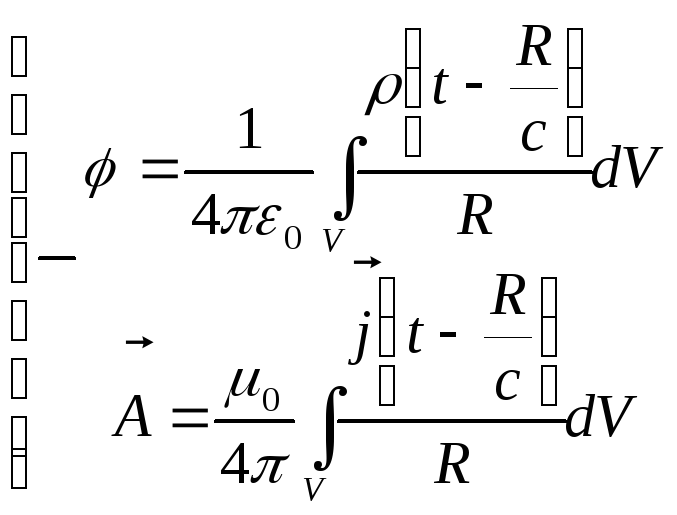(1)

Дійсно, оскільки вирази для густини заряду і густини струму, які входять в (1) є функціями часу запізнювання. Для обчислення потенціалів в момент часу t необхідно у відповідних інтегралах брати значення цих величин у різні моменти часу в кожній точці простору.

Однак якщо точка спостереження знаходиться досить далеко від системи рухомих зарядів, тобто коли віддаль від точки спостереження набагато перевищує розміри системи, вирази (1) допускають певне спрощення.

Розглянемо систему зарядів у об’ємі V:

r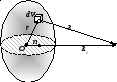— радіус вектор елементу об’єму dV із зарядом dq, R—радіус вектор точки P відносно

елемента об’єму dV, n—одиничний вектор в напрямку R₀.

Будемо шукати поле в точці P.

На великих віддалях від джерела ЕМХ можна вважати плоскими. Причому, ця віддаль повинна не тільки перевищувати розміри системи, але і бути більшою від довжини випромінюваної хвилі. Про цю область поля говорять як про хвильову зону випромінювання.

Для плоскої ЕМХ :

(2)

Для визначення H, E досить обрахувати A (1.2)

З рисунка видно, що R=R₀-r

або

(3)

оскільки r<<R₀, то величиною (r/R₀)² можна знехтувати

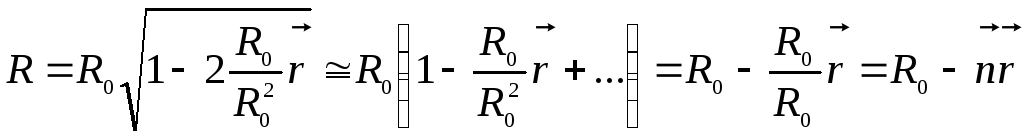
тобто

R=R₀-nr(4)

Підставимо (4) у (1.2) і оскільки R≈R₀ то у знаменнику замінимо R на R₀. У чисельнику цього робити не можна, оскільки невідомо, як змінюється j за час nr /c

(5)

З формули (5) видно, що час запізнення складається з двох частин. Перша з них, дорівнює R₀/c і називається часом запізнювання системи, описує час, необхідний для поширення ЕМП від початку координат до точки спостереження. Друга частина дорівнює nr/c і називається власним запізненням; описує час, який необхідний для поширення поля в межах системи.

Будемо розглядати випадки, коли можна знехтувати величиною nr/c в підінтегральному виразі (5):

1).

За порядком величини, nr/c ≈L/c , де L- розміри системи. При R₀>>L власне запізнення nr /c по абсолютній величині мале в порівнянні з R₀/c

nr/c << R₀/c (6)

Таким чином, якщо L<<R₀, це може бути однією з умов , при якій можна знехтувати власним запізненням.

2).

Щоб це виконувалося, необхідно щоб за час nr /c , протягом якого поле , яке поширюється із швидкістю c, пройшло по системі , заряди в системі , які рухаються із швидкістю v , не встигли помітно переміститися . За час nr/c заряди проходять шлях приблизно рівний vnr /c ≈v(L/c). Якщо цей шлях малий в порівнянні з розмірами системи, можна вважати , що за час власного запізнення розміщення зарядів у системі не встигає змінитися.

Таким чином можна вважати , що при v(L/c)<< L, або при швидкостях руху , які задовольняють нерівність

v<<c (7)

зміна конфігурації за час запізнення дуже мала.

Умову (7) можна записати і в іншому вигляді .

3).

Нехай Т означає порядок величини часу, протягом якого розподіл зарядів у системі змінюється помітним чином. Випромінювання цієї системи буде, очевидно, мати період порядку Т.

Власний час nr /c ≈L/c.

Для того, щоб за цей час розподіл зарядів у системі не встиг значно змінитися, необхідно, щоб L/c<<T. Але cT є не що інше як довжина хвилі λ випромінювання. Таким чином умову L<<cT можна записати у вигляді

L<< λ (8)

тобто розміри системи повинні бути малі в порівнянню з довжиною випромінюваної хвилі.

Якщо використати ці умови то у виразі для векторного потенціалу можна знехтувати власним запізненням:

Будемо передбачати, що умови (6), (7) та (9) виконуються, і займемося вивченням випромінювання на далеких віддалях від випромінюючої системи. На таких віддалях поле можна розглядати як плоску хвилю, і тому для визначення поля досить обчислити лише векторний потенціал.