Тема III. Постійний електричний струм.

1. Диференціальна форма законів Ома і Джоуля-Ленца

2. Умови стаціонарності струмів

3. Рівняння неперервності (Закон збереження заряду

4. Фактори існування постійного струму.

1. Диференціальна форма законів Ома і Джоуля-Ленца

1.Провідники електрики - такі тіла, в яких при наявності відмінного від нуля електричного поля (E≠0) виникає електричний струм, тобто напрямлений рух зарядів.

Обмежимося лише одним класом провідників – металами. Характерна особливість проходження струму через металеві провідники – в останніх не відбувається хімічні процеси, як , наприклад, в електролітах. Пояснюється ця відмінність тим, що в електролітах носіями зарядів є іони або групи атомів, а у металах - ,,вільні” заряди (електрони, що відщепилися від атомів).

Основний закон постійного струму – закон Ома.

, (1)

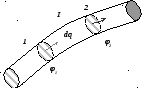
де I – сила струму в провіднику, R – опір певної ділянки цього провідника, φ₁, φ₂ - значення потенціалу біля початку, кінця цієї ділянки. При цьому силою струму називають кількість електрики, яка протікає через переріз провідника за одиницю часу, а напрям струму умовно вважається співпадаючим з тим напрямом, в якому під дією поля повинні б рухатися позитивні заряди; іншими словами, умовно вважається, що струм тече від вищого потенціалу до нижчого.

Звичайно, завжди мається на увазі перенесення повного заряду із врахуванням знаків. Можна сказати, що рух нейтрального тіла пов’язаний з перенесенням заряду надзвичайної величини (приблизна 10⁵ кулонів на грам речовини). Однак, струму в дійсності немає, тому що рухається в точності однакове число позитивних і негативних елементарних частинок з однаковою середньою швидкістю.

Сила струму вимірюється в Амперах. Струм силою в 1А переносить через переріз провідника заряд 1 кулон в секунду.

1A=1K/c

Що стосується опору R, то його розмірність з (1) така:

1 Ом=1В/A

Провідники мають опір 1 Ом, якщо при різниці потенціалів на його кінцях в 1 В по ньому протікає струм силою 1 А.

Різницю потенціалів φ₁-φ₂, яка входить у формулу (1) можна виразити через лінійний інтеграл напруженості поля E , взятий від початкового до кінцевого перерізу провідника

, (2)

де dl - елемент довжини провідника.

Лінійний інтеграл напруженості електричного поля між точками 1 і 2 називається напругою і позначається U₁₂:

, (3)

Об’єднаємо (1),(2),(3), отримаємо

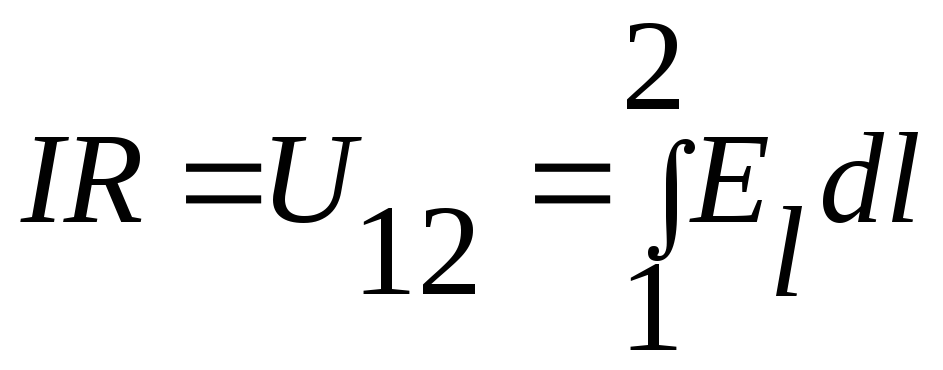, (4)

Досить важливе значення має також густина струму j ; за визначенням вона дорівнює кількості електрики , яка протікає за 1с через одиничний , перпендикулярний до струму, переріз провідника. В однорідному циліндричному провіднику

, (5)

Використовуючи поняття густини струму , ми можемо виразити основне рівняння електричного струму в диференціальній формі, яка встановлює зв’язок між величинами , які відносяться до однієї певної точки провідника, тоді як закон Ома в інтегральній формі (1) пов’язує величини, що стосуються різних точок (φ₁ і φ₂) або до скінчених відрізків провідника.

Для однорідного тонкого циліндричного провідника

, (6)

де l – довжина ділянки провідника, який має опір R, S –його переріз , ρ- питомий опір, який характеризує речовину провідника .

Якщо замість питомого опору провідника ввести обернену величину – питому провідність, або електропровідність σ : σ=1/ρ

то,

, (7)

Вносячи (7) в (8), отримаємо:

або враховуючи (5)

Таким чином

, (8)

Тут враховано, що провідник однорідний,

.

В кожній точці провідника напрям струму струму співпадає з напрямом електричного поля, яке обумовлює рух зарядів. Таким чином, вектор густини струму повинен співпадати за напрямом з вектором Е і рівність (8) можна переписати:

, (8*)

Співвідношення (8*) називається диференціальною формою закону Ома (хоча в нього і не входять похідні), тому що воно встановлює зв’язок між величинами, які відносяться до однієї певної точки провідника.

Рівняння (8*) описує поведінку струму самих звичайних речовин в певному діапазоні умов. Вивести його з фундаментальних законів електричного поля немає можливості.

До системи прикладемо постійне в часі однорідне електричне поле Е, тому на кожен носій заряду діє cила—сила така ж, як би заряд був нерухомий. Це значить, що кожен носій заряду q, незалежно від свого руху, відчуває дію постійної сили qE .

Тут ми зупинимося, щоб здивуватися! Оскільки постійна сила, що діє на вільний носій заряду, повинна викликати постійне прискорення. Але постійна густина струму означає не постійне прискорення, а постійну швидкість. Якщо наша сила дійсно підкоряється закону Ома, то це повинно відбуватися із-за того, що для наших носіїв швидкість пропорційна силі, Таким чином, носії заряду не можуть рухатися вільно: щось повинно перешкоджати руху, який зумовлений електричним полем. Сила тертя, яка перешкоджає руху—це зіткнення носіїв заряду один з одним і з довільними іншими частинками середовища.

2.При проходженні струму по провіднику , як відомо, виділяється тепло (нагрівання провідників) в колі струму.

Якщо сила струму в провіднику I, то за момент часу dt через кожен переріз провідника, протікає dq=Idt одиниць електрики. Робота, яка при цьому здійснюється

, (9)

де лінійний інтеграл може бути взятий на осі циліндричного провідника. Згідно закону збереження енергії, еквівалентна цій роботі електричних сил кількість енергії повинна виділитися у вигляді іншої форми енергії (наприклад, у формі тепла).

Таким чином, енергія, яка виділяється струмом , дорівнює

звідки

, (10)

Використовуючи закон Ома (4), отримаємо

Q=RI², (11)

Якщо поле має потенціал φ , як це має місце для постійних струмів, то ми можемо згідно (2) записати

Q=I(φ₁-φ₂)(12)

Якщо провідник нерухомий і якщо в ньому не відбувається хімічних реакцій, то ця кількість енергії Q виділяється струмом у формі тепла. Тому рівняння (10) (11) і (12) виражають закон Джоуля ( Джоуля – Ленца).

Закон Джоуля – Ленца (11) носить характер інтегрального закону , але його, подібно до закону Ома, можна перетворити у диференціальну форму. Для цього замість Q введемо питому потужність струму q , тобто кількість тепла, яка виділяється за секунду в одиниці об’єму провідника

q=Q/V, (13)

Розглянемо знову однорідний циліндричний провідник перерізом S, довжиною l. Об’єм V=Sl. Тоді

, (14)

Тут використано, те що

.

Таким чином, j=σE, то

, (15)

Формула (15) – закон Джоуля – Ленца у диференціальній формі (застосовний до провідників, незалежно від їх форми, однорідності і.т.д. і незалежно змінні чи постійні струми).