Konspekt lekcil

при n=1;

при n>1;

Втаблиці приведені значення дисконтних множників для різних видів

ставок.

99

Аналогічним чином отримаємо систему нерівностей для дисконтних множників:

при n>1.

Безперервне нарощування та дисконтування, безперервні проценти

Впрактичних фінансово-кредитних розрахунках безперервне нарощування, тобто нарощування за безкінечно малі відрізки часу,

застосовуються дуже рідко.

Суттєво більше практичне значення безперервне нарощування має в аналізі складних фінансових проблем, наприклад при обґрунтованому виборі інвестиційних рішень та при здійсненні фінансового проектування.

При неперервному нарахуванні процентів застосовують особливий вид процентної ставки - силу росту. Сила росту характеризує відносний приріст нарощуваної суми за безкінечно малий проміжок часу. Вона може бути постійною або змінюватись в часі.

Постійна сила росту

Згадаємо, що при дискретному нарахуванні процентів m раз на рік за номінальною ставкою j нарощена сума знаходиться як:

чим більше значення m, тим менший проміжок між моментами нарахування процентів. При гранично маленькому проміжку часу, тобто при m що прямує до нескінченості отримуємо:

В даному випадку нарощувана сума знаходиться як:

S = P e j n

Для того, щоб відрізнити неперервну ставку від дискретної силу росту прийнято позначати як δ. Тепер можна записати формулу в кінцевому вигляді:

S = P e n

Дискретні та неперервні ставки нарощування знаходяться у функціональній залежності між собою. З рівності множників

= ln ( 1+ i)

нарощування ( 1+ i )n = e випливає, що:

Наприклад, сума на котру нараховуються проценти, дорівнює 2000000

i = e - 1

грн., сила росту 10%, термін 5 років.

Нарощена сума в даному випадку буде складати:

S = 2 000 000 * e0.1* 5 = 3 297 744.25.

Неперервне нарощування за ставкою δ =10% рівнозначно нарощенню за

i = e0.1 - 1= 0.1051709

даний термін складних річних процентів за ставкою:

101

ми дійсно отримуємо ту саму нарощену суму якщо застосуємо складні проценти при даній ставці:

S = 2 000 000 ( 1+ 0.1051709 )5 = 3 297 744.25.

Для того, щоб знайти дисконтний множник на основі сили росту розв'яжемо рівняння відносно P:

P = S e- n

Отже дисконтний множник дорівнюватиме e- n .

Змінна сила росту Нехай сила росту змінюється в часі у відповідності до певного закону -

безперервній функції часу t = f ( t ) , тоді нарощена сума та сучасна вартість визначатимуться за формулами:

n

S = P e t dt

0

n

P = S e- t dt

0

Розглянемо варіанти визначення множника нарощування для випадків,

t = 0 + a t

коли величина t являє собою лінійну та експоненціальну функції. Якщо лінійна функція задана рівнянням:

де 0 - початкове значення сили росту; a - приріст сили росту;

то отримуємо формулу:

102

q = e 0 + a n2

2

множник нарощування в цьому випадку буде знаходитись як:

Наприклад, нехай початкове значення сили росту дорівнює 8%, ставка безперервно та лінійно змінюється, приріст за рік становить 2% (а = 0.02). Термін нарощування - 5 років. Для розрахунку множника нарощування за п'ять років знайдемо його степінь:

0.08* 5 + 0.02* 52 = 0.65 2

множник нарощування становитиме . Продовжимо даний приклад. Допустимо, що сила росту лінійно зменшується, тобто: а = -0.02. В даному випадку ступінь множника нарощування дорівнює 0.15, відповідно:

e0.15 = 1.16183.

Розглянемо ситуацію коли сила росту змінюється по закону геометричної прогресії:

t = 0 * at

де 0 - початкове значення сили росту; a - постійний темп росту.

В даному випадку ступінь множника дорівнює:

а сам множник нарощування буде знаходитися як:

103

q = eln 0a * ( an - 1 )

Наприклад, початковий рівень сили росту 8%, процентна ставка безперервно збільшується (річний приріст 20%, тобто а = 1.2), термін - 5 років. Ступінь множника нарощування за весь термін дорівнюватиме:

0.08 * (1.25 - 1 )= 0.65305 ln 1.2

відповідно e0.65305= 1.9214 .

Визначення терміну платежу та процентних ставок При розробці умов фінансових задач ми часто зустрічаємося з

необхідністю розв'язання зворотних задач - розрахунку тривалості позики та рівня процентної ставки. Розглянемо операції зі складними процентними ставками та розв'яжемо рівняння, що пов'язують величини P та S відносно величин, котрі нас цікавлять.

Термін платежу

Приведемо формули для розрахунку n для різних умов нарощування процентів та дисконтування. При нарощуванні за складною річною ставкою і та за номінальною ставкою j відповідно отримаємо:

У випадку дисконтування за складною обліковою ставкою d та за номінальною обліковою ставкою f можемо використати формули:

104

У випадку нарощування при постійній силі росту δ та при змінній з постійним темпом силі росту, можемо використати формули:

Наприклад, визначимо за який термін, сума, що дорівнює 75000000 грн. досягне 200000000 грн. При нарахуванні процентів за складною ставкою 15% раз в рік та поквартально. За вище наведеними формулами отримаємо:

Величина процентної ставки

Наведемо формули для розрахунку ставок i, j, d, f, δ для різних умов нарощування процентів та дисконтування. Вони отримуються при розв'язку відповідних рівнянь, що визначають S та P, відносно ставок.

При нарощуванні процентів за складною річною ставкою та за номінальною ставкою проценту m раз на рік знаходимо формули:

105

При дисконтуванні за складною обліковою ставкою та номінальною

При нарощуванні та при постійній силі росту:

При нарощуванні за змінною з постійним темпом силі росту використовуємо формулу:

Наприклад, ощадний сертифікат куплений за 100 тис. грн., викупна його сума 300 тис. грн., термін 2.5 роки. Визначимо який рівень доходності інвестицій в вигляді річної ставки складних процентів. За вище наведеною формулою знаходимо:

i = 2.5 100300 - 1= 0.55184,… Њ 55.184%

106

Наприклад, термін погашення векселя дорівнює два роки. Дисконт при його зарахуванні склав 30%. Знайдемо якій складній обліковій ставці відповідає даний дисконт, якщо P/S=0.7. За вище наведеною формулою знаходимо:

d = 1 - 0.7 = 0.16334,… Њ16.334%

Криві доходності Будь-яка позикова чи кредитна операція передбачає використання

деякого значення процентної ставки, на яку погодились обидві сторони, що приймають участь у даній операції. Значення даної ставки залежить від багатьох факторів.

Найбільш важливим фактором при цьому є ризик неповернення позики. В свою чергу даний ризик також залежить від ряду факторів, найважливішим з яких є термін операції.

При всіх інших рівних умовах операція з терміном 5 років є більш ризиковою, ніж аналогічна однорічна операція.

Компенсувати величину ризику власникові фінансових ресурсів може підвищена дохідність даної фінансової операції.

Таким чином, залежність типу дохідність - ризик можна умовно замінити залежністю дохідність - термін, котру отримати для використання з практичною метою суттєво легше.

Дану залежність представлену у вигляді графіку називають кривою доходності.

При цьому на графіку по вертикалі відкладають дохідність Y, а по горизонталі термін n так як це показано нижче на рис. 16.

У випадку, коли графік охоплює широкий діапазон термінів, то для виміру терміну застосовують логарифмічну шкалу.

107

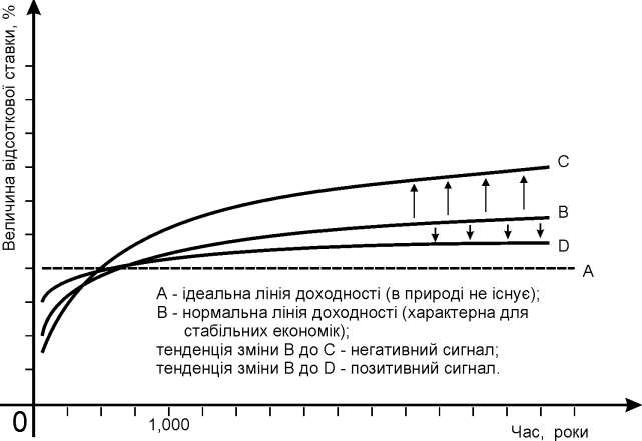
Рис. 16. Графічна модель ліній доходності (залежність величини відсоткової ставки від терміну операції)

Значення доходності, котрі спостерігаються, в більшості випадків знаходяться коло кривої або на ній.

Конкретна крива дохідності відповідає ситуації, що склалася на ринку на даний момент часу і характерна для короткого часового періоду. Зміна економічної ситуації змінює форму кривої та її відповідне положення на графіку.

Для нормальної економічної ситуації дана крива має форму А, як це показано на малюнку. Дохідність повинна зростати по мірі збільшення терміну інвестицій. При цьому кожна наступна зміна терміну операції на одиницю дає все менше збільшення доходності.

Криву доходності такого типу називають додатною або нормальною кривою доходності. Нормальна форма кривої спостерігається в умовах, коли інвестори в своїй масі враховують такі фактори, як скорочення терміну ліквідності та ріст невизначеності фінансових результатів при збільшенні терміну фінансової операції.

108