2.4. Степінь вершини графа

Нехай G(V)- неорієнтований граф.

Визначення. Степенем(a) деякої вершиниa  Vназивається кількість ребер графу, інцидентних цій вершині.

Якщо граф заданий матрицею суміжності вершин, то

(1)

Для матриці інцидентності аналогічна формула має вигляд

(2)

Число ребер у графі Gпозначимо черезv_E = v_E(G). При підрахунку сумикожне реброe(v_i, v_j), графуGпідраховується двічі: один раз – як таке, що з’єднує вершинуv_iзv_j, а другий раз – як таке, що з’єднуєv_jзv_i. Тому

(3)

(формула (3) залишається правильною і для графу з петлями, якщо їх розглядати як подвійні ребра).

Оскільки в лівій частині формули (3) стоїть парне число, то це означає, що у скінченному графі без петель кількість вершин з непарним степенем – парна.

Визначення. Граф називається однорідним степеняk, якщо (v_i = k), для всіхv_i  V.

В однорідному графі кількість ребер згідно з формулою (3) v_E = nk/2.

Визначення. Повний графU = U(V)- це неорієнтований граф, у якому дві довільні вершини з’єднані рівно одним ребром.

Зрозуміло, що повний граф U(V)зnвершинами – це однорідний граф степеня(n ‑ 1). Томуv_E = n(n –1) / 2.

Визначення. Повний граф з петлямиU₀ = U₀(V)- це повний граф, у якому до кожної вершини додана петля.

Кількість ребер у повному графі з петлями v_E(U₀) = v_E(U) + n = n(n +1) / 2.

Нехай тепер G(V)- орієнтований граф. Тоді через(v_i) і*(v_i) позначають кількість ребер, які виходять з вершиниv_iі входять в вершинуv_iвідповідно.

Аналогічно попередньому кількість ребер в орієнтованому графі

.

2.5. Частини, суграфи і підграфи графу.

Операції з частинами графу

Визначення. ГрафНназивається частиною графуG(позначаєтьсяH  G), якщо:

а) V(H)  V(G);

б) E(H)  E(G).

Визначення. ГрафНназивається суграфом графуG, якщо він є частиною графуGі

V(H) = V(G).

На Рис. 4 зображені граф Gі його три частини. ГрафH3є суграфом.

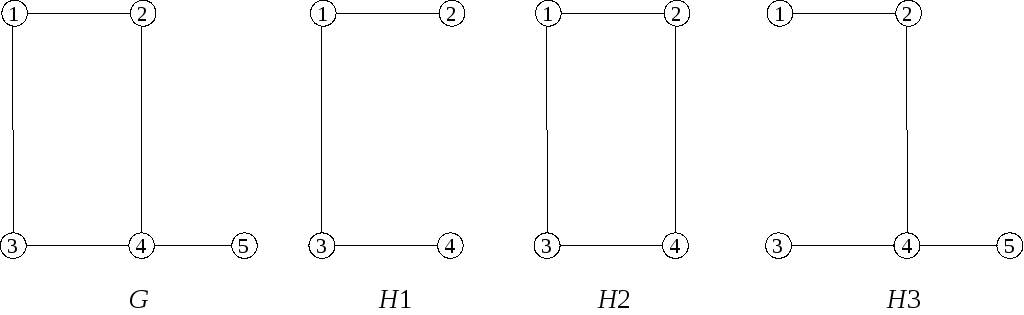
Рис.4.

Визначення. СуграфHназивається покриваючим для графуG, якщо будь-яка вершинаHінцидентна хоча б одному ребру зG. Зауважимо, що якщо в графіGє ізольовані вершини, то для нього не існує покриваючого графуH.

Визначення. ПідграфомG(U) графуG(V) називається така його частина, яка містить всі ребра графуG(V), що з’єднують дві будь-які вершини з множиниU.

На рис. 4 H1 не є підграфомG(не містить реброe(2, 4)), аH2 – підграф графуG.

Визначення. Зірковим графом, який визначається деякою вершиноюa  V, називається граф, що містить всі ребра даного графуG(V), інцидентні вершині „a”.

За аналогією з операціями поміж множинами можна виконувати і операції між графами.

Визначення. ЯкщоH– частина графу, то(доповнення графуH) – це граф, в який входять всі ребра графуG, які не належатьH:

.

Визначення. НехайH₁іH₂- дві частини графуG. ТодіH = H₁  H₂(об’єднання або сума) це також частина графуG, яка складається зі всіх ребер, що належать абоH₁абоH₂.

Визначення. НехайH₁іH₂- дві частини графуG. ТодіH = H₁  H₂(перетин) це частина графуG, яка складається зі всіх ребер, що належатьH₁таH₂одночасно.

Визначення. Якщо дві частиниH₁іH₂графуGне мають спільних вершин, то їх сумаH = H₁  H₂називається прямою. ЯкщоH₁іH₂не перетинаються по ребрах, то їх сума називається прямою по ребрах.

Наприклад: - пряма сума за ребрами.