
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •1.1 Величины, характеризующие электрические процессы
- •1.2 Классификация электрических цепей
- •1.3 Идеальные неавтономные двухполюсные элементы цепей
- •1.4 Идеальные автономные элементы цепей
- •1.5 Законы Кирхгофа
- •1.6 Схемы замещения реальных цепей
- •1.7 Схемы замещения с зависимыми источниками
- •1.8 Основы топологии цепей
- •1.9 Основные принципы и теоремы теории электрических цепей
- •1.10 Эквивалентные преобразования однотипных элементов
- •А Последовательное соединение однотипных элементов
- •Б Параллельное соединение однотипных элементов
- •Контрольные вопросы
- •2.1 Схемы замещения при постоянных воздействиях
- •2.2 Метод уравнений Кирхгофа
- •2.3 Метод узловых напряжений
- •2.4 Метод наложения
- •2.5 Метод эквивалентного генератора
- •2.6 Метод контурных токов
- •Контрольные вопросы
- •3.1 Классификация электрических сигналов
- •Индуктивный элемент
- •Емкостный элемент
- •3.5 Векторное представление
- •Контрольные вопросы
- •4.1 Представление гармонических колебаний
- •4.2 Уравнения пассивных элементов в комплексной форме
- •Резистивный элемент
- •Индуктивный элемент
- •Емкостный элемент
- •4.3 Основные законы теории электрических цепей
- •4.5 Матричный метод анализа электрических цепей
- •4.6 Анализ цепей со связанными индуктивностями
- •4.6.1 Магнитные связи в электрических цепях
- •4.6.2 Последовательное соединение связанных индуктивностей
- •4.7 Баланс мощностей
- •4.9 Энергетические характеристики сигналов
- •Контрольные вопросы
- •5.1 Нелинейные элементы и их характеристики
- •5.2 Способы описания характеристик нелинейных элементов
- •5.3 Методы анализа нелинейных цепей
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 1.2
- •Лабораторная работа № 1.3
- •Лабораторная работа № 1.4
- •Лабораторной работе № 1.1
- •Лабораторная работа № 1.2
- •Лабораторная работа № 1.3
- •Лабораторная работа № 1.4
- •Уравнения Кирхгофа
- •Анализ цепи с одним источником энергии
- •Метод наложения
- •Метод узловых напряжений
- •Метод эквивалентного источника
- •Дуальные преобразования
- •Метод комплексных амплитуд
- •Анализ нелинейных цепей
23
Напряжением холостого хода автономного двухполюсника называется напряжение, которое имеет место на его зажимах, когда они разомкнуты, т.е. когда ток, протекающий через эти зажимы, равен нулю.
Током короткого замыкания автономного двухполюсника называется ток, протекающий между его зажимами, когда они соединены накоротко.
Теорема обратимости (взаимности). Все пассивные линейные цепи обла-
дают интерсивным свойством, которое называют обратимостью. Это свойство доказывается с помощью теоремы обратимости. Доказательство этой теоремы можно найти в учебниках по теории цепей [4, 5, 6].
Существует два варианта этой теоремы.
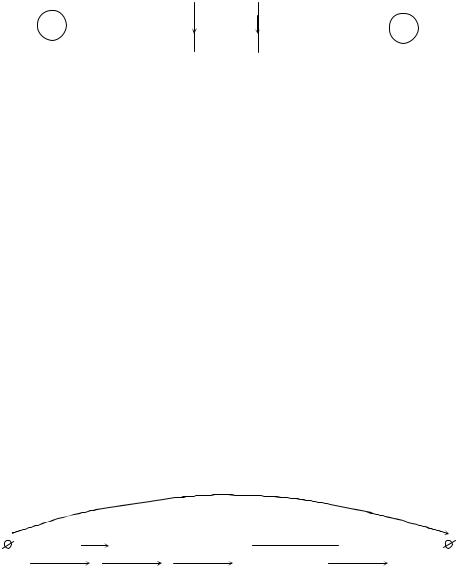
Вариант первый с источником напряжения: если в какую-либо ветвь пассивной электрической цепи (ПЭЦ) включить источник напряжения Е (рис. 1.14, а), то в другой ветви будет протекать ток I2. Если теперь поменять местами контуры и включить этот же источник напряжения во вторую ветвь (рис. 1.14, б), то в первой будет иметь место ток I1.
|
|
|
|
|
|
|
|
+Е2 |
Е1 |
+ |
ПЭЦ |
|
I2 I1 |
ПЭЦ |
|
||
|
|
|
|
|
|
|
|
|
|
|
a) |
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
Рисунок 1.14 – Пассивная электрическая цепь при включении источника напряжения:
а – слева; б – справа
Если источник напряжения один и тот же (Е1 = Е2), и токи I2 = I1 одинаковые величины, то это говорит о том, что электрическая цепь обратима.
Второй вариант дуален и заключается в том, что вместо источников напряжения подключают источник тока, а определяют напряжение на режимах холостого хода во втором контуре. Это свойство позволяет облегчить анализ электрических цепей и будет рассмотрен далее в разделе „Матричный метод анализа электрических цепей”.
1.10 Эквивалентные преобразования однотипных элементов
А Последовательное соединение однотипных элементов
Последовательное соединение сопротивлений. Соединение элементов,
показанное на рис. 1.15, является последовательным (все элементы соединяются между собой с помощью устранимых узлов).
|
|
R1 |
|
R2 |
|
R3 |
|
|
Rn |
|
Uab |
|
a+ |
|
i |
|
|
|
_ |
||||||
|
|
|
|
|
|
|
|
|
|
b |
||
|
|
|
|
|
|
|
|
|
||||
|
u1 |
|
u2 |
|
u3 |
|
|
un |
||||
|
|
|
|
|
|
|
|
|
||||
Рисунок 1.15 – Последовательное соединение элементов R

24
Напряжение на каждом из сопротивлений рис. 1.15 определяется законом Ома:
u1 = R1 i; u2 = R2 i; u3 = R3 i … un = Rn i.
Общее напряжение на всем участке ab определится как арифметическая сумма напряжений на каждом из сопротивлений:
uab = R1 i + R2 i + R3 i +…+ Rn i = i(R1+ R2 + R3+…+ Rn) = iRЭ ,
а |
i |
RЭ |
b |
|
uab
Рисунок 1.16 – Эквивалентное сопротивление
где RЭ – это эквивалентное сопротивление участки "аb" (рис. 1.16), равное арифметической сумме всех сопротивлений участка "аb".
Последовательное соединение индуктивностей. Это соединение изобра-
жено на рис. 1.17.
+ |
L1 |
L2 |
L3 |
Ln |
Uab _ |
|
i |
|
|
b |
|
a |
u1 |
u2 |
u3 |
un |
Рисунок 1.17 – Последовательное соединение индуктивностей
На каждой из индуктивностей будет иметь место соответственно напряже-
ние
u1 = L1 dtdi ; u2 = L2 dtdi и т. д.
Напряжение на участке ab выразится формулой
uab = L1 dtdi + L2 dtdi + L3 dtdi +K+ Ln dtdi = dtdi (L1 + L2 + L3 +K+ Ln )= dtdi LЭ ,
а+ |
i |
LЭ |
– |
|
uab |
b |
Рисунок 1.18 – Эквивалентная индуктивность
где LЭ – эквивалентная участку аb индуктивность (рис. 1.18), равная арифметической сумме всех индуктивностей участка аb.
Последовательное соединение емкостей. Это соединение изображено на рис. 1.19.
|
|
C1 |
|
|
|
|
|
|
Uab |
_ |
|||
+ i |
|
|
|
C2 |
|
|
C3 |
|
|
Cn |
|||
|
|
|
|
|
|
|
_ |
||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
||||
u |
1 |
u2 |
u3 |
un |
|
||||||||
Рисунок 1.19 – Последовательное соединение емкостей
25
На каждой емкости будет иметь место соответственно напряжение
|
|
|
|
|
|
u1 = |
1 |
|
idt ; u |
|
= |
1 |
|
idt |
и т. д. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
C1 ∫ |
2 |
C2 |
∫ |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Напряжение на участке аb выразится формулой |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
1 |
1 |
|
|
|
1 |
|
|
|
|
1 1 1 |
|
1 |
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
uab = |
|
∫idt+ |
|
∫idt+ |
|
∫idt+K+ |
|
∫idt = ∫idt |
|
+ |
|
+ |
|
|
+K+ |
|
|
= ∫idt |
|
, |
|||||||
C |
C |
C |
C |
C |
C |
C |
C |
C |
|||||||||||||||||||
1 |
2 |
3 |
|
|
|
n |
|
|
|
|
|
1 |
|
|
2 |
3 |
|
|
n |
|
Э |
|
|||||
где 1/СЭ – величина, обратная эквивалентной емкости (рис. 1.20) на участке ab:
|
|
|
|
|
|
|
|
|
|
+ |
i |
|
СЭ |
– |
||
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
= |
1 |
+ |
1 |
+ |
1 |
+K+ |
1 |
; |
а |
|
|
|
|
|
b |
|
|
|
|
|
||||||||||||
uab |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
CЭ |
С1 |
С2 |
С3 |
Сn |
Рисунок 1.20 – Эквивалентная |
|||||||||||
емкость
Последовательное соединение идеальных источников напряжения.
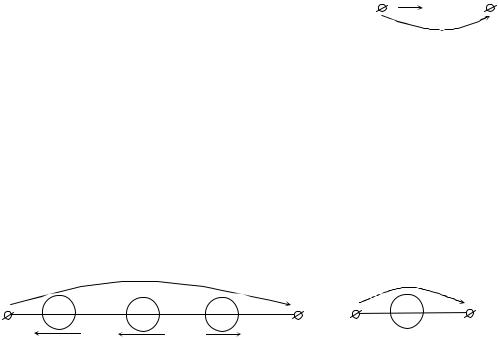
При последовательном соединении независимых источников напряжения они заменяются одним эквивалентным источником напряжения с задающим напряжением ЕЭ, равным алгебраической сумме задающих напряжений отдельных источников. Причем со знаком "+" берутся задающие напряжения, совпадающие с задающим напряжением эквивалентного источника, а со знаком "–" – несовпадающие рис. 1.21.
Пример соединения трех источников приведен на рис. 1.21.
|
|
|
u12 |
2 1 + |
u12 |
1 |
+ |
+ |
+ |
2 |
|
|
Е1 |
Е2 |
Е3 |
|
ЕЭ |
|
|
а) |
|
|
б) |
Рисунок 1.21 – Эквивалентное преобразование идеальных источников напряжения:
а– последовательное соединение источников;
б– эквивалентный источник
На основании второго закона Кирхгофа,
u12 = EЭ = −E1 − E2 + E3.
Б Параллельное соединение однотипных элементов
Используя принцип дуальности, можно получить формулы эквивалентных параметров параллельного соединения однотипных элементов. Этот анализ предлагается проделать самостоятельно.
