
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •1.1 Величины, характеризующие электрические процессы
- •1.2 Классификация электрических цепей
- •1.3 Идеальные неавтономные двухполюсные элементы цепей
- •1.4 Идеальные автономные элементы цепей
- •1.5 Законы Кирхгофа
- •1.6 Схемы замещения реальных цепей
- •1.7 Схемы замещения с зависимыми источниками
- •1.8 Основы топологии цепей
- •1.9 Основные принципы и теоремы теории электрических цепей
- •1.10 Эквивалентные преобразования однотипных элементов
- •А Последовательное соединение однотипных элементов
- •Б Параллельное соединение однотипных элементов
- •Контрольные вопросы
- •2.1 Схемы замещения при постоянных воздействиях
- •2.2 Метод уравнений Кирхгофа
- •2.3 Метод узловых напряжений
- •2.4 Метод наложения
- •2.5 Метод эквивалентного генератора
- •2.6 Метод контурных токов
- •Контрольные вопросы
- •3.1 Классификация электрических сигналов
- •Индуктивный элемент
- •Емкостный элемент
- •3.5 Векторное представление
- •Контрольные вопросы
- •4.1 Представление гармонических колебаний
- •4.2 Уравнения пассивных элементов в комплексной форме
- •Резистивный элемент
- •Индуктивный элемент
- •Емкостный элемент
- •4.3 Основные законы теории электрических цепей
- •4.5 Матричный метод анализа электрических цепей
- •4.6 Анализ цепей со связанными индуктивностями
- •4.6.1 Магнитные связи в электрических цепях
- •4.6.2 Последовательное соединение связанных индуктивностей
- •4.7 Баланс мощностей
- •4.9 Энергетические характеристики сигналов
- •Контрольные вопросы
- •5.1 Нелинейные элементы и их характеристики
- •5.2 Способы описания характеристик нелинейных элементов
- •5.3 Методы анализа нелинейных цепей
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 1.2
- •Лабораторная работа № 1.3
- •Лабораторная работа № 1.4
- •Лабораторной работе № 1.1
- •Лабораторная работа № 1.2
- •Лабораторная работа № 1.3
- •Лабораторная работа № 1.4
- •Уравнения Кирхгофа
- •Анализ цепи с одним источником энергии
- •Метод наложения
- •Метод узловых напряжений
- •Метод эквивалентного источника
- •Дуальные преобразования
- •Метод комплексных амплитуд
- •Анализ нелинейных цепей
89
ПРИЛОЖЕНИЕ Б
Примеры решения задач модуля 1
Уравнения Кирхгофа
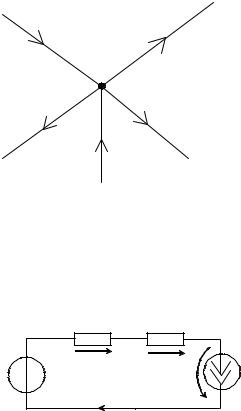
Задача 1 В узле электрической цепи сходятся ветви, направление токов в которых и их значения приведены на схеме.
Необходимо определить неизвестный ток I5.
Решение |
|
I1 |
|
|||||
|
5A |
|||||||
Запишем уравнение по первому за- |
|
|||||||
|
|
|
|
|
|
I2 |
||
кону Кирхгофа для данного узла: |
|
|
|
|
|
|
8A |
|
I1 − I2 − I3 + I4 − I5 = 0 , |
|
|
|
|
|
I3 |
||
откуда |
I5 |
|
|
|
|
|
|
|
|
|
|
11A |
|||||
I5 = I1 − I2 − I3 + I4 = |
|
|
|
I4 |
|
|||
=5 −8 −11 + 3 = −11A. |
|
|
|
3A |
||||
Проверка:
5 – 8 – 11 + 3 – (– 11) = 0, Рисунок 1.1 – Исследуемый узел
0 ≡ 0.
|
|
Уравнения Кирхгофа |
|
|
|
|
|
|
Задача |
2 Дана электрическая цепь |
|
|
R1 |
R2 |
|
|
|
(рис. 2.1): R1 |
= 10 Ом, R2 |
= 20 Ом, Е = 15 В, |
E |
+ |
u1 |
|
|
|
J = 1 A. |
|
|
u2 |
uj |
J |
|||
|
|
|
|
|||||
Определить uj. |
|
|
|
|
I |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
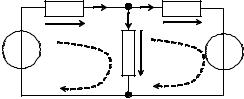
Рисунок 2.1 – Исследуемая цепь
Решение
Направление тока I в данной схеме совпадает с направлением тока источника тока J. Тогда напряжения U1 и U2 направлены как показано на рисунке и равны соответственно:
U1 = I R1 =1 10 =10B;
U2 = I R2 =1 20 = 20В.
Запишем уравнение по второму закону Кирхгофа для данного контура:
U1 +U2 +U j − E = 0;
U j = E −U1 −U2 =10 −10 − 20 = −10B.
Знак „минус” означает, что направление напряжения источника тока обратно указанному на схеме.
|
|
|
|
|
90 |
|
R1 I1 |
I2 |
R2 |
|
Задача 3 Определить токи в ветвях |
||
E1 + u1 |
|
I3 |
|
E2 |
методом уравнений Кирхгофа для цепи |
|
R3 |
u2 |
рис. 3.1. |
||||
|
u3 |
|
|
Дано: R1 = 10 Ом, R2 = 20 Ом, |
||
|
К1 |
|
К2 |
+ |
R3 = 30 Ом, Е1 =20 В, Е2 =10 В. |
|
|
|
|
|
Для данной схемы можно записать |
||
Рисунок 3.1 – Исследуемая цепь |
||||||
одно независимое уравнение по первому |
||||||
закону Кирхгофа и два – по второму закону. Для этого выберем произвольно направления токов I1, I2, I3. как показано на рис. 3.1 и направления обходов контуров, как показано на этом рисунке штриховыми стрелками. В результате, на основании первого и второго законов Кирхгофа, получим систему уравнений вида
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Узел: I1 − I 2 − I3 |
= 0; |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К1 |
U 1 + U 3 − E1 = 0; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К2 |
U 2 − E2 −U 3 = 0. |
||||
|
|
Выразим напряжения U1, U2, U3 через токи и сопротивления: |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 − I2 − I3 = 0; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 R1 + 0 + I3 R3 = E1; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 + I2 R2 − I3 R3 = E2. |
|||||
Теперь токи I1, I2, I3 можно определить с помощью определителей: |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 = ∆1 ; I2 |
= ∆2 ; I3 |
= |
∆3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
∆ |
|
∆ |
|||||||
|
|
−1 |
−1 |
|
|
|
|
|
−1 |
−1 |
|
|
|
|
|||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||
∆ = |
|
R1 |
0 |
R3 |
|
= |
|
10 |
0 |
30 |
= −600 −[10 (30 + 20)] = −1100; |
||||||||||||||
|
|
0 |
R2 |
− R3 |
|
|
|
|
0 |
20 |
− 30 |
|
|
|
|
||||||||||
|
|
0 |
−1 |
−1 |
|
|
|
|
= −E1[R3 − R2 ]+ E2 [− R3 ]= −20 (50) +10 (−30) = −1000 −300 = −1300; |
||||||||||||||||
|
|
|
|
||||||||||||||||||||||
∆1 = |
|
|
|
|
|
E1 |
0 |
R3 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
E2 |
R2 |
− R3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
0 |
−1 |
|
|
= −E1[− R3 ]− E2 [R3 + R1 ]= 20(−30) −10(40) = −600 − 400 = −1000; |
||||||||||||||||
|
|
|
|||||||||||||||||||||||
∆2 = |
|
R1 |
E1 |
R3 |
|
|
|||||||||||||||||||
|
|
|
|
0 |
E2 |
− R3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
−1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
∆3 = |
|
R1 |
0 |
E1 |
|
=−E1 R2 +E2 R1 =−20 20+10 10=−400+100=−300; |
|||||||||||||||||||
|
|
0 |
R2 |
E2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

|
|
|
|
|
|
|
|
|
91 |
|
I1 |
= |
1300 |
=1,182A , I2 |
= |
1000 |
= 0,91A , I3 = |
|
300 |
= 0,273A . |
|
1100 |
1100 |
1100 |
||||||||
|
|
|
|
|
|
|||||
Проверку найденных токов можно произвести с помощью баланса мощностей:
∑Pk =0 ,
или Рист = Рпотр.
− I1 E1 − I2 E2 + I12 R1 + I22 R2 + I32 R3 = 0.
После подстановки значений убеждаемся в правильности полученных значений токов. Эту операцию советуем проделать самостоятельно.
Анализ цепи с одним источником энергии
Задача 4 Определить токи ветвей и напряжения на элементах цепи, схема которой изображена на рис. 4.1. Параметры элементов следующие:
Е = 6 В, R1 = 5 Ом, R2 = 30 Ом, R3 = 10 Ом, R4 = 20 Ом.
I1 |
R1 |
|
I3 |
R3 |
|
|
U1 |
|
I2 |
U3 |
|
|
|
|
U4 |
||
E |
|
R2 |
U2 |
R4 |
|
Рисунок 4.1 – Исследуемая цепь |
|
||||
|
|
|
Решение |
|
|
|
|
|||
1 Обозначим направления токов и |
|
R1 |
|
I2 |
|
|
||||
напряжений, как показано на схеме |
|
I1 |
|
|
|
|||||
|
|
|
I3 |
|
|
|||||
рис. 4.1. |
|
|
|
|
U1 |
|
|
|
||
2 Так как цепь содержит последо- |
|
|
|
R34 |
U34 |
|||||
E |
R2 |
U2 |
||||||||
вательно-параллельные |
|
соединения |
||||||||
элементов, то воспользуемся методом |
|
|
|
|
|
|
||||
эквивалентных преобразований. Со- |
|
|
|
|
|
|
||||
противления R3 и R4 на схеме рис. 4.1 |
|
Рисунок 4.2 – Эквивалентное |
|
|||||||
соединены последовательно; их можно |
|
преобразование рис. 4.1 |
|
|||||||
заменить одним эквивалентным сопро- |
|
|
|
|
|
|
||||
тивлением R34, величина которого |
|
|
|
|
|
|
||||
R34 = R3 + R4 = 10 + 20 = 30 Ом. |
|
|
|
|
||||||
После преобразования схема приобретает вид рис. 4.2. |
|
|
|
|||||||
В данной схеме сопротивления R2 и |
R34 соединены параллельно. Заменим |
|||||||||
их одним эквивалентным сопротивлением R234: |
|
|
|
|
||||||
R |
|
= R2 R34 = 30 30 =15 Ом |
|
|
|
|||||
234 |
|
R2 + R34 |
30 + 30 |
|
|
|
|
|||
|
|
|
|
|
|
|
||||
При этом U2 =U34 =U3 +U4 . Токи в ветвях определим по формуле „чужого” |
||||||||||
сопротивления: I2 = I1 R |
R34 |
; I3 = I1 |
R |
R2 |
|
|
|
|
||
+ R |
+ R . |
|
|
|
|
|||||
2 |
|
34 |
2 |
34 |
|
|
|
|
||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
92 |
|
I1 |
R1 |
|
|
|
|
|
|
|
Преобразованная схема приобретает вид |
||||||||||
|
|
|
|
рис. 4.3. |
|
|
|
|
|
|
|
|
|
|
||||||
+ |
|
|
|
|
|
|
|
|
|
Схема рис. 4.3 содержит последователь- |
||||||||||
|
U1 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
ное соединение источника напряжения и двух |
|||||||||||||||
|
|
|
|
|
||||||||||||||||
E |
R234 |
|
|
U234 |
|
сопротивлений. Ток в цепи и напряжения на |
||||||||||||||
|
|
|
|
|
|
|
|
элементах определим по закону Ома: |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
I |
|
= |
|
E |
= |
|
6 |
= 0,3A; |
|
Рисунок 4.3 – Эквивалентное |
|
|
|
|
1 |
|
|
|||||||||||||
|
|
|
|
R1 |
+ R234 |
5 |
+15 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
преобразование цепи 4.2 |
|
|
|
|
U1 = I1 R1 = 0,3 5 =1,5B; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Определим токи I2 и I3 (см. выше) |
U2 = I1 R234 = 0,3 15 = 4,5B. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
I2 |
= 0,3 |
30 |
|
|
= 0,15A; |
|
|
|
|
|||||
|
|
30 +30 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
I |
|
= 0,3 |
|
30 |
= 0,15A. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
3 |
|
30 +30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По закону Ома определим напряжения
U3 =I 3 R3 = 0,15 10 =1,5 B;
U4 =I 3 R4 = 0,15 20 = 3 B.
3 Проверку расчетов можно выполнить, составив уравнение баланса мощностей для исходной цепи:
−E I1 + I1 U1 + I2 U2 + I3 U3 + I4 U4 = 0.
Подставим значения и произведем расчеты:
−6 0,3 + 0,3 1,5 + 0,15 4,5 + 0,15 1,5 + 0,15 3 = 0;
−1,8 + 0,45 + 0,675 + 0,225 + 0,45 = 0;
−1,8 +1,8 = 0;0 ≡ 0.
Проверка подтвердила правильность расчетов.
|
|
|
|
|
Метод наложения |
|
I1 |
R1 |
1 I |
R3 |
|
2 I |
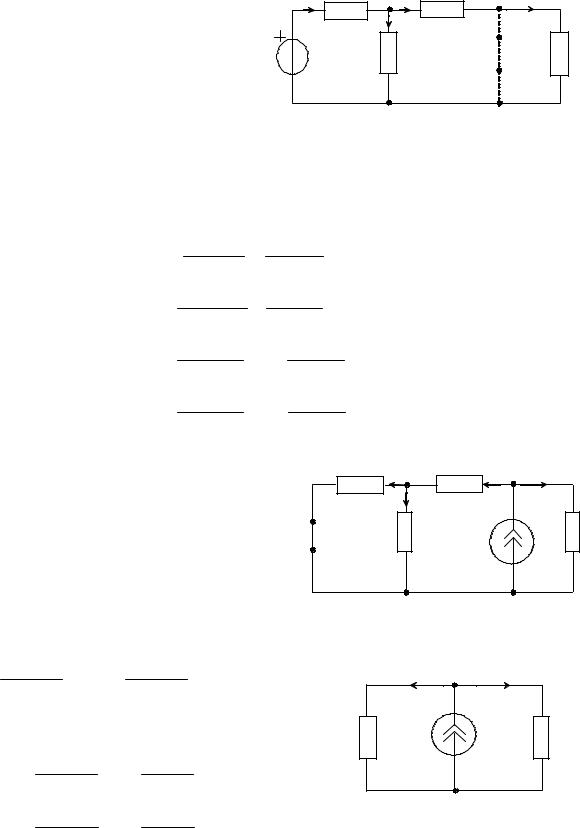
Задача 5 Методом наложения |
|
определить токи ветвей цепи, схема |
|||||
|
I2 |
3 |
|
4 |
||
|
|
|
J |
|
которой изображена на рис. 5.1. Па- |
|
E |
|
R2 |
|
R4 |
раметры элементов следующие: |
|
|
|
|
||||
|
|
|
|
|
|
Е = 6 В; I = 0,6 A; R1 = R2 = 20 Ом; |
|
|
|
|
|
|
R3 = R4 = 10 Ом. |
3
Рисунок 5.1 – Исследуемая цепь
93
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
||
1 Зададимся условно положи- |
|
|
|
R |
|
R3 |
|
|
|||||||||
тельными направлениями токов, как |
|
|
′ |
I3′ |
|
I4 |
|||||||||||
показано на рис. 5.1. |
|
|
|
|
|
|
|
|
I1 |
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
I2′ |
|
|
|
||||
2 Положим задающий ток ис- |
|
E |
|
R2 |
ХХ |
R4 |
|||||||||||
точника тока равным нулю (J = 0). |
|
|
|||||||||||||||
При этом источник тока заменим хо- |
|
|
|
|
|
|
|
|
|||||||||
лостым ходом. Получим первую ча- |
|
|
Рисунок 5.2 – Цепь с одним |
||||||||||||||
стную схему с одним источником |
|
|
|||||||||||||||
энергии (рис. 5.2). |
|
|
|
|
|
|
|
|
|
|
источником напряжения |
|
|||||
Для определения частных токов |
|
|
|
|
|
|
|
|
|||||||||
I1′− I3′ воспользуемся результатами предыдущей задачи: |
|
|
|
||||||||||||||
|
|
|
R34 = R3 +R4 =10 +10 = 20 Ом; |
|
|
|
|
||||||||||
|
|
|
R |
|
= |
|
R2 R34 |
= |
20 20 |
=10 Ом; |
|
|
|
||||
|
|
|
|
234 |
|
|
R2 + R34 |
|
20 + 20 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
I1′ = |
R1 |
E |
= |
6 |
10 |
= 0,2A; |
|
|
|
||||
|
|
|
|
|
|
|
+ R234 |
|
20 + |
|
|
|
|
|
|||
|
|
|
I2′ = I1′ R |
R34 |
|
|
20 |
|
|
|
|
|
|||||
|
|
|
+ R |
= 0,2 20 + 20 = 0,1A; |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
34 |
|
|
|
|
|
|
|
|
|
|
|
I3′ = I1′ R |
R2 |
|
|
20 |
|
|
|
|
||||||
|
|
|
+ R |
= 0,2 20 + 20 = 0,1A. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 |
34 |
|
|
|
|
|
|
|
|
3 Положим задающее напряжение ис- |
|
R1 |
I′′ |
R3 |
I′′ 2 |
′′ |
|||||||||||
точника напряжения равным нулю (Е = 0). |
|
||||||||||||||||
|
|
1 1 |
|
3 |
I4 |
||||||||||||
При этом источник напряжения заменим |
|
|
I2′′ |
|
|
|
|||||||||||
коротким замыканием. Получим вторую |
|
|
|
|
J |
R4 |
|||||||||||
частную схему с одним источником энер- |
КЗ |
R2 |
|
||||||||||||||
гии (рис. 5.3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем схему рис. 5.3. Заменим |
|
|
|
|
|
|
|||||||||||
параллельно-последовательное |
соединение |
|
|
0 |
|
|
|
||||||||||
сопротивлений R1, R2, R3 эквивалентным |
|
Рисунок5.3 – Цепьсодним |
|||||||||||||||
сопротивлением R123: |
|
|
|
|
|
|
|
|
|
|
источникомтока |
|
|||||
R123 = R1 R2 |
+ R3 |
= 20 20 |
+10 = 20 Ом. |
|
|
I 3′′ |
1 |
I 4′′ |
|
||||||||
R1 + R2 |
20 + 20 |
|
|
|
|
|
|
|
|
|
|||||||
Используя формулу „чужого” сопро- |
R123 |
J |
|
R4 |
|||||||||||||
тивления, определим токи: |
|
|
|
|
|
|
|
|
|||||||||
I3′′ = I |
|
R4 |
= 0,6 |
|
10 |
|
|
= 0,2 A; |
|
|
|
|
|
|
|
||
|
R13 + R4 |
|
20 +10 |
|
|
|
|
|
|
0 |
|
|
|||||
|
|
R13 |
|
|
20 |
|
|
|
|
|
|
|
|
|
|
||
I4′′ = I |
|
= 0,6 |
|
|
|
= 0,4 A; |
|
|
Рисунок 5.4 – Эквивалентное |
||||||||
|
R13 + R4 |
|
20 +10 |
|
|
|
|
преобразование цепи рис. 5.3 |
|||||||||
