Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Одесская национальная академия связи им. А.С. Попова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Модуль 1.pdf

Скачиваний:

101

Добавлен:

10.02.2016

Размер:

1.56 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2313 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

то, в соответствии с уравнением индуктивного элемента u = L dtdi ,

возникает напряжение

+ ϕ +

ϕ+

u = ωLIm cos ωt

ωLIme

Тогда

j ϕ+

U&mL

ωLIme

= ωLe j

2 .

Ime jϕ

По формуле Эйлера

I&mL

e j 2

= j .

Подставив это значение в последнее выражение, получаем

или

ZL = jωL

(4.4)

ZL = jX L .

Емкостный элемент

Аналогично для емкостного элемента

= − j

или

jωC

ωC

ZC = − jX C .

(4.5)

4.3Основные законы теории электрических цепей

вкомплексной форме

Приведенные выше уравнения пассивных элементов в комплексной форме имеют одинаковую структуру:

U&mR = I&mR R; U&mL = I&mL ZL ; U&mC = I&mC ZC ;

Поэтому выражения
U&m = I&m Z;		(4.6a)
и
U& = I&Z, a I& =U Y ,		(4.6б)
где	1
Y =	1
Y =	Z
	Z

называют законом Ома в комплексной форме для амплитудных и дейст-

вующих значений. При этом для комплексных токов и напряжений сохраняется

та же система направлений отсчета, которая принята для мгновенных значений токов и напряжений. Согласно первому закону Кирхгофа (ЗТК), в любом узле цепи, находящейся в режиме гармонических колебаний,

l	l
∑ik = ∑Imk cos(ωt + ϕik )= 0 .
k=1	k=1

Заменив мгновенные значения токов ik их комплексными амплитудами I&mk , по-

лучим:

– для амплитудных значений тока

l
∑I&mk	= 0	(4.7а)
k =1
и
– для действующих значений тока.
l
∑I&k = 0.		(4.7б)
k =1
Аналогично по второму закону Кирхгофа, для любого контура
n
∑U&mk	= 0	(4.8а)
k =1
и
n
∑U&k	= 0.	(4.8б)

k =1

Отсюда следует, что существует полная аналогия в записи основных законов для цепей постоянного тока и для цепей, находящихся в режиме гармонических колебаний. Поэтому все методы анализа цепей постоянного тока формально справедливы и для цепей при гармонических воздействиях.

4.4 Система узловых уравнений для комплексных амплитуд

Рассмотрим анализ цепи в режиме гармонических колебаний методом узловых напряжений.

В канонической форме записи система уравнений для комплексных амплитуд колебаний отличается от системы, составленной для цепи постоянного тока, только обозначениями. Для упрощения обозначений вместо комплексных

амплитуд U&m , I&m принято составлять уравнения для комплексных действую-

щих значений

U& = U&2m = U2m e jϕu =Ue jϕu , I& = I&m2 = Im2 e jϕi = Ie jϕi .

Часто вместо термина „комплексное действующее значение напряжения или тока” принято говорить „комплексное напряжение” или „комплексный ток”.

Таким образом, система уравнений для комплексных узловых напряжений имеет вид:

1	Y11U&1 −Y12U&2 −... −Y1NU&N = J&11;
2	−Y U&	1	+Y U&	2	−Y U&	3	−... −Y	U&	N	= J&	22	;
	21	1	22	2	23	3	2N		N		22
	........................................................											(4.9)
N	−YN1U&1 −YN 2U&2 −YN 3U&3 −... +YNNU&N = J&NN ,

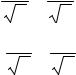
где Ykk представляет собой сумму комплексных проводимостей ветвей, сходящихся в узле k; а Ykl = Ylk – комплексную проводимость ветви, включенной между k-м и l-м узлами. На рис. 4.3 дан фрагмент некоторой цепи. Проводимость ветви, соединяющей между собой узлы k и l, имеет вид:

	Y =	1	+	1	+ jωC		.
	kl	jωL		R		kl
		kl		kl
	Lkl				Для остальных методов предла-
	Lkl				гается самостоятельно записать вы-
					гается самостоятельно записать вы-
	Rkl (Gkl)				ражения в комплексной форме.
k	Rkl (Gkl)	l			При машинных методах анализа
k		l			цепей в гармоническом режиме ис-
					цепей в гармоническом режиме ис-
	Ckl				пользуются подпрограммы для вы-
	Ckl				числения проводимостей и сопро-
					числения проводимостей и сопро-
Рисунок 4.3 – Параллельная RLC цепь					тивлений типовых пассивных двух-
					полюсников, составляющих эти це-

пи.

4.5 Матричный метод анализа электрических цепей

Математической основой этой темы является элементарная теория матриц. Поэтому, прежде чем приступить к изучению этой темы, необходимо посмотреть соответствующий раздел математики.

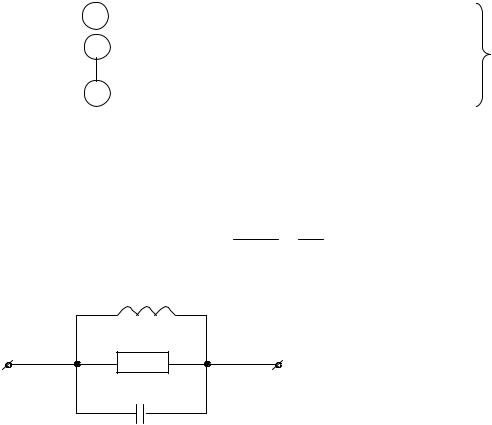
Введем понятие проходной четырехполюсник (2×2-полюсник) и его рассматриваем с позиции определения связей между входными и выходными то-

ками и напряжениями ( I&1,U&1, I&2 , U&2 ) попарно. Очевидно, что коэффициенты, связывающие эти величины, будут либо безразмерные (İ1↔İ2, U&1 ↔U&2 ), либо

иметь размерность сопротивлений или проводимостей ( I& ↔U& ). Число различных форм уравнений получается шесть, т. е. шесть систем параметров 2×2- полюсников. Для разных случаев применяют ту или иную систему. При записи

уравнений будем считать токи I&1 и I&2 втекают в четырехполюсник, а напряжение U&1 и U&2 направленные от верхних зажимов к нижним, как показано на рис. 4.4, а.

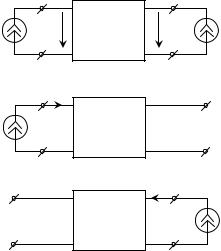
В качестве примера выведем одну из систем параметров. Пусть 2×2-полюсник подключен к некоторой цепи. В этой цепи есть источник, значит, на зажимах рассматриваемого четырехполюсника будут напряжения и токи. Запишем уравнения, связывающие между собой напряжения

U&1 и U&2 и токи İ1 и İ2. На основании тео-

ремы замещения (компенсации) можем заменить внешнюю цепь двумя источниками

тока с задающими токами J&1 и J&2 (рис.

4.4, а). Применим к полученной цепи принцип наложения (рис. 4.4, б и в):

&	&′	&′′	(4.10)
U1	=U1	+U1	(4.10)
U&2 =U&2′ +U&2′′

Для схемы рис. 4.4, б можно записать:

				51
J&1	U&1	(2×2)	U&2	J&2
		а)
		I&1
J&	U&′	(2×2)		&′
1	1			U 2

	б)	I&2
		I&2
U&1′′	(2×2)	U&2′′	J&2

в)

Рисунок 4.4 – Четырехполюсник:

а– с двумя источниками тока;

б– с одним источником слева;

в– с одним источником справа

U&1′ = Z11I&1;		(4.11)
U&2′ = Z21I&1,		(4.11)
U&2′ = Z21I&1,
а для схемы рис. 4.4, в можно записать:
U&1′′= Z12 I&2	;	(4.12)
U&2′′ = Z22 I&2.		(4.12)
U&2′′ = Z22 I&2.

Подставим уравнения (4.11) и (4.12) в (4.10) и получим искомые уравне-

ния.

U&1 = Z11I&1 + Z12 I&2 ;

U&2 = Z21I&1 + Z22 I&2.

Коэффициенты Z в этих уравнениях называются Z параметрами. В общем случае они комплексные и зависят только от конфигурации 2×2-полюсника и величин его элементов. Если эти уравнения решить относительно токов İ1, İ2, то получим уже другую систему параметров и т. д.

В таблице 4.1 приведены все шесть систем параметров, приведены физические соответствия коэффициентов.

Таблица 4.1 – Системы параметров 2×2-полюсника

Системы уравнений

Физический смысл коэффициентов

I&1

I&2

I&1

I&2

I&1=Y11U&1 +Y12U&2

U&1

КЗ

U&2

Y =

I&1

Y =

I&2

I&2=Y 21U&1 +Y 22U&2

U&1

U&2 = 0

U&2

U&1 = 0

I&2

I&1

= 0

U 2

U&1

I&1

U&1

I&2

ХХU&2

ХХ

U&2

11 1

U&1

=Z I&

Z =

21 1

= 0

U& 2

U&2

= 0

U&1

I&1

U&1

I&1

I&2

ХХU&2

КЗ

U&1

A =

= 0

U 2

− I

U 2

I&2

I&1

= 0

2= 0

− I

U 2

U&1

I&1

I&2

I&1 =F11U&2+F12I&2

ХХU&2

КЗ

U&2

I&1

F =

I&1

U& 2=F 21U&2+F 22I&2

U&1

I&2= 0

−I&2

U&1 = 0

U&2

= 0

− I

I&1

I&2

U&1

КЗ U&1

ХХ

U&2

11 1

U&1

=H I&

+H U&

H =

21 1

= 0

U 2

I1 = 0

H 21 =

I&2

H 22 =

I&2

= 0

Окончание таблицы 4.1

Системы уравнений

Физический смысл коэффициентов

U&1

I&2

I&1

I&2

ХХ

U&2

КЗ

U&2

B =

= 0

B21

I&2

B22 =

I&2

= 0

Если речь идет об одном и том же 2×2-полюснике, то зачастую необходимо переходить от одной системы параметров к другой, т. е. иметь формулы, выражающие связи между различными системами параметров. В таблице 4.2 дана связка формул, выражающих указанные связи.

Таблица 4.2 – Связи систем параметров

Z 22

Z 12

∆A

Y11

Y12

−

∆

−

∆

Y21

Y22

−

Z 21

Z11

−

A11

∆Z

Y 22

Y 12

A11

∆A

∆

− ∆

−

A21

Y 21

Y 11

Z21

Z22

A22

−

∆Y

−

A21

− Y 22

Z 11

−

∆Z

A11

A12

Y 21

Z 21

−

∆Y

Y 11

−

Z 22

A21

A22

Y 21

Z 21

−

Y 12

∆Z Z12

A12

∆A

Y 11

Z 22

A22

Y 21

∆y

−

Z 21

−

A21

Y 11

Z 22

Z22

A22

∆Y

Y 12

−

Z12

A21

∆A

Y 22

Z11

Z 11

A11

−

Z 21

∆Z

−

A12

Y 22

Z11

Z 11

A11

−

H 12

∆F

F 12

H 11

F 22

H 21

∆H

−

F 21

H 11

F 22

∆H

−

H 12

−

F12

H 22

F11

F 11

H 21

F 21

∆F

H 22

F11

−

∆H

H 11

−

F 22

H 21

F 21

−

H 22

−

F 11

∆F

H 21

F 21

H11

H12

F 22

−

F12

∆F

−

F 21

F11

∆F

H 22

−

H 12

∆H

−

H 21

H 11

∆H

Подобно тому, как соединяются между собой двухполюсники, четырехполюсники тоже можно соединять между собой несколькими способами. А именно: существует пять видов соединения четырехполюсников. В таблице 4.3 при-

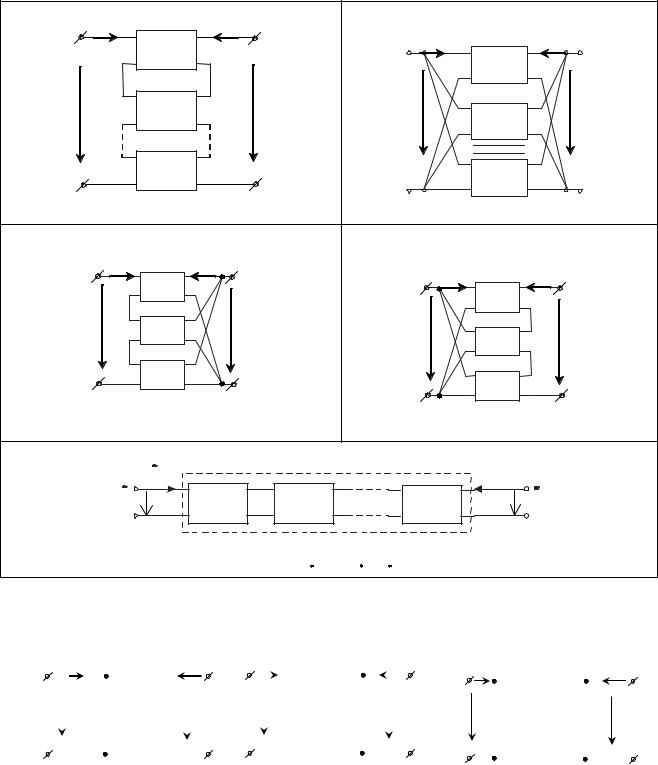
						54
ведены способы соединения четырехполюсников, и указаны системы парамет-
ров, которые использоваться при этом.
Таблица 4.3 – Способы соединения четырехполюсников
Последовательное				I&1	Параллельное
Последовательное						I&
I&1	(1)	I&2				I&
I&1	(1)	I&2			(1)	2
					(1)
U&1	(2)	U&2		&	(2)	&
				U1	(2)	U 2
	(n)				n
					n
[Z ] =[Z (1) ] +[Z (2) ] +K+[Z (n) ]				[Y ] =[Y (1) ] +[Y (2) ] +K+[Y (n) ]
Последовательно – параллельное				Параллельно – последовательное
	I&1	I&		Параллельно – последовательное
	I&1	I&			&	&
	(1)	2			I1	I2
	(1)				(1)
					(1)
U&1	(2)	U&2		U&1	(2)	U&2
	(n)				(n)
					(n)
[H ] =[H (1) ] +[H (2) ] +K+[H (n) ]				[F ] = [F (1) ] +[F (2 ) ] +K+[F ( n) ]
			Каскадное
	I1	(1)	(2)		I2
	U1	(1)	(2)	(n)		U2
		[ A] =[A(1) ] [ A(2) ]		K [ A(n) ]
Рассмотрим несколько примеров определения матриц 2×2-полюсников.
Дана цепь в виде 2×2-полюсника. Определим его матрицу [Y].

U&1

U 2

Y Y

+Y )

−Y

Y Y

−Y

[Y]=

Y Y

+Y )

−Y

[Y]=

Y Y

−Y

Y Y

−Y

+Y )

Y Y

−Y

+Y )

а)

б)

в)

Рисунок 4.5 – Примеры четырехполюсников:

а – Г-образный; б – Г-образный повернутый; в – П-образный

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 2313 14 15 16 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.12.20184.08 Mб5Методичний посібник до лб_Поштовий переказ чере....doc
#
10.02.2016609 Кб16МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУК2 - копия.docx
#
01.04.2025118.77 Кб0Министерство транспорта и связи Украины.docx
#
06.09.2019370.69 Кб3МК з підприємницької практики.doc
#
10.02.201651.2 Кб17Модель OSI.doc
#
10.02.20161.56 Mб101Модуль 1.pdf
#
10.02.20161.61 Mб180Модуль 2.pdf
#
10.02.20161.56 Mб150Модуль 3.pdf
#
10.02.20161.39 Mб40Модуль 4.pdf
#
24.08.201975.66 Кб11модульна робота.docx
#
01.04.202514.56 Mб2мой курсак по ЛП.doc