
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •1.1 Величины, характеризующие электрические процессы
- •1.2 Классификация электрических цепей
- •1.3 Идеальные неавтономные двухполюсные элементы цепей
- •1.4 Идеальные автономные элементы цепей
- •1.5 Законы Кирхгофа
- •1.6 Схемы замещения реальных цепей
- •1.7 Схемы замещения с зависимыми источниками
- •1.8 Основы топологии цепей
- •1.9 Основные принципы и теоремы теории электрических цепей
- •1.10 Эквивалентные преобразования однотипных элементов
- •А Последовательное соединение однотипных элементов
- •Б Параллельное соединение однотипных элементов
- •Контрольные вопросы
- •2.1 Схемы замещения при постоянных воздействиях
- •2.2 Метод уравнений Кирхгофа
- •2.3 Метод узловых напряжений
- •2.4 Метод наложения
- •2.5 Метод эквивалентного генератора
- •2.6 Метод контурных токов
- •Контрольные вопросы
- •3.1 Классификация электрических сигналов
- •Индуктивный элемент
- •Емкостный элемент
- •3.5 Векторное представление
- •Контрольные вопросы
- •4.1 Представление гармонических колебаний
- •4.2 Уравнения пассивных элементов в комплексной форме
- •Резистивный элемент
- •Индуктивный элемент
- •Емкостный элемент
- •4.3 Основные законы теории электрических цепей
- •4.5 Матричный метод анализа электрических цепей
- •4.6 Анализ цепей со связанными индуктивностями
- •4.6.1 Магнитные связи в электрических цепях
- •4.6.2 Последовательное соединение связанных индуктивностей
- •4.7 Баланс мощностей
- •4.9 Энергетические характеристики сигналов
- •Контрольные вопросы
- •5.1 Нелинейные элементы и их характеристики
- •5.2 Способы описания характеристик нелинейных элементов
- •5.3 Методы анализа нелинейных цепей
- •Контрольные вопросы
- •Литература
- •Лабораторная работа № 1.2
- •Лабораторная работа № 1.3
- •Лабораторная работа № 1.4
- •Лабораторной работе № 1.1
- •Лабораторная работа № 1.2
- •Лабораторная работа № 1.3
- •Лабораторная работа № 1.4
- •Уравнения Кирхгофа
- •Анализ цепи с одним источником энергии
- •Метод наложения
- •Метод узловых напряжений
- •Метод эквивалентного источника
- •Дуальные преобразования
- •Метод комплексных амплитуд
- •Анализ нелинейных цепей
43
Так же как и в индуктивной, в емкостной цепи происходит обмен энергией между источником и емкостью. Поступая от источника, энергия запасается в электрическом поле емкости и затем возвращается к источнику при исчезновении электрического поля.
В заключение следует отметить, что определения действующих значений тока и напряжения (3.3), а также средней мощности за период (3.13) справедливы для периодических напряжений и токов любой формы.
Из рассмотренного выше режима гармонических колебаний в линейных электрических цепях следует очень важный вывод: если в линейной цепи, содержащей R, L, C элементы, действует гармонический источник некоторой частоты ωи, то напряжения и токи, возникающие на всех участках этой цепи, изменяются также по гармоническому закону с той же частотой.
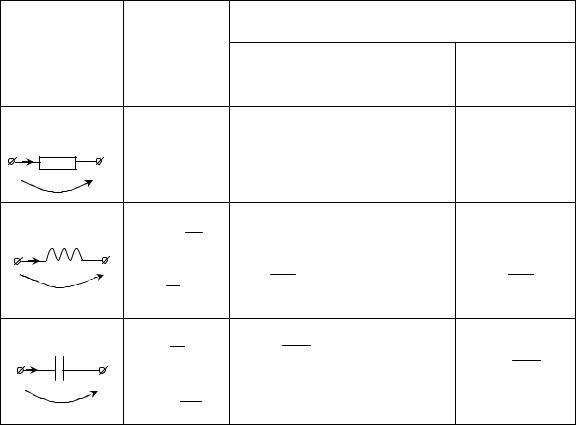
В табл. 3.1 приведены уравнения элементов цепи во временной форме для мгновенных и действующих значений при гармоническом режиме.
Таблица 3.1 – Уравнения элементов цепи |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Временная |
|
|
|
|
|
|
|
Гармонический режим |
|
|
|
|||||||
Элемент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
форма |
|
|
|
|
|
|
|
|
|
|
|
|
действующие |
||||||||
|
|
|
|
|
мгновенные значения |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значения |
|||
Резистивный |
uR = Ri |
|
|
uR = RIm cos(ωt + ϕ) |
|
|
|
|
|
|
|
||||||||||
i |
G |
|
|
|
|
|
|
U = RI |
|
||||||||||||
|
R |
uR |
iR = Gu |
|
|
iR = GU m cos(ωt + ϕ) |
|
|
|
I = GU |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Индуктивный |
uL = L di |
uL = ωLIm cos(ωt + ϕ) |
|
|
|
U = ωLI |
|
||||||||||||||
i |
L |
|
|
|
|
|
|||||||||||||||
|
|
|
dt |
|
|
|
|
1 |
|
|
|
|
π |
|
1 |
|
|
||||
|
uL |
|
|
1 |
t |
i |
|
= |
|
|
U |
|
I = |
U |
|||||||
|
|
iL = |
∫udt |
L |
ωL |
m |
cos ωt + ϕ − |
|
|
ωL |
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||||||
|
|
|
|
L −∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Емкостный |
uC = C1 |
t |
|
uC = |
|
1 |
Im cos(ωt + ϕ) |
|
|
|
|
|
|
|
|||||||
−∫∞idt |
|
|
|
|
|
|
1 |
|
|
||||||||||||
i |
C |
|
|
ωC |
|
|
|
U = |
|
I |
|||||||||||
|
uС |
|
iC =C du |
|
|
|
|
|
|
|
|
|
|
π |
|
ωC |
|
||||
|
|
|
|
|
|
|
|
|
|
|
I = ωLU |
|
|||||||||
|
|
|
iC = ωCUm cos ωt + ϕ + |
2 |
|
|
|||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.5 Векторное представление |
|
|
|
|
|
|
|
||||||||||
|
|
гармонических колебаний одной частоты |
|
|
|
||||||||||||||||
При анализе электрических цепей векторное представление гармонического колебания является более удобной формой, чем временное.
Выше отмечалось, что в линейной цепи с гармоническим источником некоторой частоты ωи все токи и напряжения имеют также гармонический харак-
44
тер той же частоты. Это позволяет при анализе цепи исключить частоту ωи из числа аргументов колебаний токов и напряжений и характеризовать их только двумя параметрами – амплитудой и начальной фазой. При этом каждому колебанию ставится в соответствие вращающийся вектор определенной длины с заданной начальной фазой. Эти векторы изображаются в полярной системе координат и все операции над ними выполняются в соответствии с векторной алгеброй.
1 i |
R 2 |
L |
3 C 4 |
u |
u R |
u L |
uc |
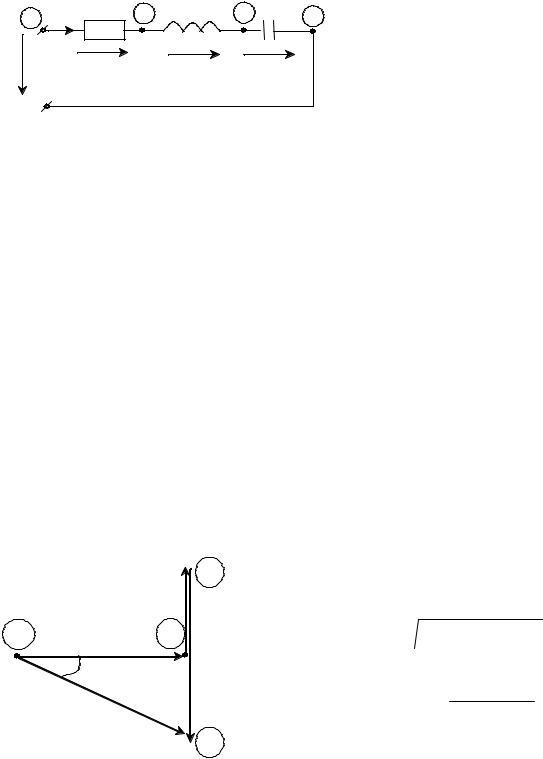
Рисунок 3.9 – Последовательная RLC цепь
i = Im cosωt
Применение векторного представления гармонических колебаний предлагается рассмотреть на примере цепи рис. 3.9.
При прохождении через эту цепь гармонического тока
на ее зажимах создается гармоническое напряжение, равное на основании второго закона Кирхгофа (ЗНК):
u = uR +uL +uC . |
|
|
||||||
В соответствии с таблицей 3.1, |
|
|
|
|
|
|
|
|
|
|
|
π |
1 |
|
π |
||
u = RIm cosωt + ωLIm cos |
ωt + |
+ |
|
|
Im cos ωt − |
. |
||
ωC |
||||||||
|
|
|
2 |
|
2 |
|||
Сумме гармонических колебаний соответствует сумма векторов |
||||||||
RIm 0 + ωLIm π + |
1 |
Im − |
π |
=Um ϕ, |
|
|||
ωC |
2 |
|
||||||
2 |
|
|
|
|
|
|||
или |
|
|
|
|
|
|
(3.21) |
|
π |
|
|
|
π |
|
|
|
|
UmR 0 +Um L 2 |
+UmC − |
2 |
=Um ϕ. |
|
||||
На рис. 3.10 представлена эта векторная сумма в полярной системе координат, причем начало каждого следующего вектора соответствует концу предшествующего. Такая векторная диаграмма называется топографической
|
3 |
|
UmL |
1 |
2 |
|
UmR |
ϕ |
UmC |
Um
4
Рисунок 3.10 – Векторная диаграмма напряжений RLC цепи
(XL < XC).
Из рис. 3.10 следует, что амплитуда приложенного напряжения:
Um =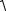 UmR2 +(UmL +UmC)2 ,
UmR2 +(UmL +UmC)2 ,
аначальная фаза его
ϕ= arctgUmL −UmC .
UmR
Располагая этими параметрами приложенного к цепи рис. 3.9 напряжения, получают его мгновенное значение
45
u =Um cos(ωt + ϕ).
Использование векторных диаграмм делает анализ цепей в гармоническом режиме наглядным и является удобным способом проверки вычислений. Пример изображения векторной диаграммы токов для параллельного контура предлагается выполнить самостоятельно.
Анализ электрических цепей с помощью векторных диаграмм обычно применяется в случае достаточно простых цепей.
Метод, позволяющий рассчитывать сложные цепи в гармоническом режиме алгебраически, был введен в электротехнику А.Е. Кеннели и П.Ч. Штейнметцем в 1893 – 1894 гг. Он получил название метода комплексных амплитуд, или символического метода. Все последующее изложение курса ТЭЦС, а также и специальных курсов базируется на этом методе. Символический метод сочетает аналитические расчеты с геометрическими представлениями.
Контрольные вопросы
1Что такое сигнал?
2Какие сигналы являются регулярными и случайными?
3Какие сигналы называются аналоговыми?
4Какие сигналы называются дискретными?
5Какие сигналы называются периодическими?
7Какое напряжение (ток) называется гармоническим?
6 Укажите вид периодичности импульсных сигналов?
8Что называется мгновенным, средним и действующим значением гармонического тока (напряжения)?
9Какими параметрами обладает гармоническое колебание?
10Что такое векторные диаграммы напряжений? Токов?
11Как отличаются начальные фазы тока и напряжения в индуктивности (емкости)?
12Какими способами можно представить гармоническое колебание?
13Что собой представляет индуктивное сопротивление, индуктивная проводимость?
14Что собой представляет емкостное сопротивление, емкостная проводи-
мость?
4 МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД ПРИ АНАЛИЗЕ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
4.1Представление гармонических колебаний
спомощью комплексных чисел
Известно, что любая точка на комплексной плоскости определяется ради- ус-вектором этой точки. Так называют вектор, начало которого совпадает с на-

+j |
Im |
|
|
46 |
|
|
чалом координат, а конец находится в точке, |
||
А2 |
А |
|
|
соответствующей данному комплексному чис- |
|
|
|
лу (рис. 4.1). |
|
|
|
|
|
В полярной, или показательной форме |
|
α |
Re |
+ |
некоторое комплексное число A& представляет- |
0 |
А1 |
|
ся как: A& = A α = Ae jα , где А – модуль, α – ар- |
гумент, j =  −1 .
−1 .
Применив формулу Эйлера, получают тригонометрическую форму записи комплекс-
ного числа: A& = Acos α + jAsin α или, соответ-
ственно, алгебраическую форму: |
|
|
|
|
|
||
A& = A + jA , |
где |
A1 = A cosα; A2 = A sinα. |
|||||
1 |
2 |
|
|
|
|
|
|
Совершенно очевидно, что: |
|
|
|
|
A2 |
|
|
|
A = |
A2 |
+ A2 |
, α = arctg |
. |
||
|
|
||||||
|
|
1 |
|
2 |
|
A1 |
|
|
|
|
|
|
|
||
Если вектор вращается против часовой стрелки с угловой скоростью ω, то в любой момент времени его положение определяется комплексной величиной
Ae |
j(ωt+α) |
& |
jωt |
, |
(4.1) |
|
= Ae |
|
где
A& = Ae jα
– комплексная амплитуда, представляющая данный вектор в момент t = 0 (рис. 4.2), т. е. A& – это комплексная величина, не зависящая от времени. Мо-
Im |
|
дуль и аргумент, соответственно, |
|||
A& еjωt |
равны амплитуде и начальной фазе |
||||
ωt |
A&(t = 0) |
гармонического колебания. |
|
||
Умножение |
комплексной ам- |
||||
α |
+Re |
плитуды |
A& на оператор вращения |
||
0 |
|
e jωt означает поворот вектора |
A& на |
||
|
|
угол ωt в положительном направле- |
|||
|
& |
нии. Из тригонометрической фор- |
|||
Рисунок 4.2 – Вращающийся вектор A |
мы комплексной |
функции |
(4.1) |
||
на комплексной плоскости |
Ae j(ωt+α) |
= Acos(ωt +α) + jAsin(ωt +α) |
|||
следует, что гармоническая функция Acos(ωt + α) |
может рассматриваться как |
||||
действительная часть комплексной функции (4.1) или как проекция вращающегося вектора на действительную ось. Условно это записывается следующим образом:
Acos(ωt +α) =Re(A&e jωt ). |
(4.2) |
