40

постоянную – UI и гармоническую U I cos2(ωt + ϕ) составляющую удво-

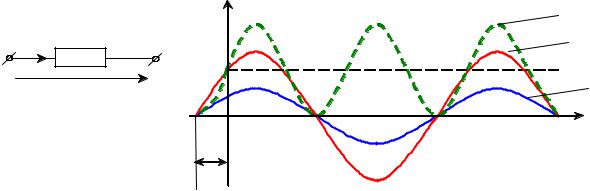
енной частоты 2ω. Так как напряжение и ток совпадают по фазе на резистивном элементе, то мгновенная мощность Р всегда положительна. Это означает, что в резисторе происходят необратимые потери энергии.

На рис. 3.6 представлены временные диаграммы тока, напряжения и мгновенной мощности на резистивном элементе.

Рисунок 3.6 – Временные зависимости u, i, p резистивного элемента: а – резистивный элемент; б – зависимости i(t), u(t), p(t)

Среднее за период Т значение мощности, выделяемой в резисторе,

называется активной мощностью и измеряется в ваттах (Вт). Из выражения (3.12) и рис. 3.6 следует, что

Индуктивный элемент

Если через индуктивный элемент протекает ток i = Im cos(ωt + ϕi ),

то соответственно уравнению индуктивного элемента, напряжение на нем:

называется индуктивной проводимостью. Следовательно,

41

Im = BLUm , I = BLU .

Из (3.15) следует, что начальные фазы тока и напряжения на индуктивном элементе отличаются на угол π/2. Принято говорить, что напряжение на индуктивном элементе опережает ток на угол π/2.

Мгновенная мощность, поступающая в индуктивный элемент, определяется выражением:

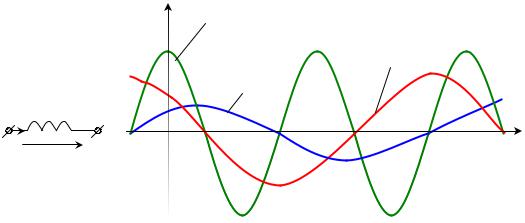
и изменяется по гармоническому закону с удвоенной частотой (в этом выражении напряжение и ток индуктивного элемента соответствуют рис. 3.7).

i, u, p p

u

i

i L

Рисунок 3.7 – Временные зависимости u, i, p индуктивного элемента: а – индуктивный элемент; б – зависимости i(t), u(t), p(t)

Наличие отрицательных значений мощности говорит о том, что индуктивность отдает энергию в течении полупериода. Очевидно, что средняя мощность за период в индуктивном элементе равна нулю.

Энергия магнитного поля индуктивности

индуктивности равен нулю и достигает максимума при амплитудном значении тока. Таким образом, происходит обмен энергией между источником и индуктивным элементом. Поступая от источника, энергия запасается в магнитном поле индуктивности и затем возвращается к источнику при исчезновении магнитного поля.

Емкостный элемент

Пусть к емкостному элементу приложено напряжение

u=Um cos(ωt + ϕu ).

Всоответствии с уравнением емкостного элемента, ток

Амплитудные и действующие значения тока и напряжения связаны соотношением:

Im = ωCU m ; I = ωCU .

Величина

Bc =ωC

имеет размерность проводимости и называется емкостной проводимостью. Обратная ей величина, соответственно, является емкостным сопротивлением

X C = ω1C .

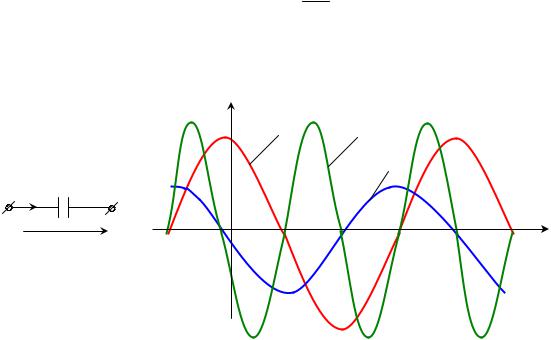
Начальные фазы емкостного тока и напряжения отличаются на угол π/2. Принято говорить, что напряжение на емкости отстает от тока на угол π/2. Временные диаграммы тока и напряжения емкости приведены на рис. 3.8.

i, u, p

Рисунок 3.8 – Временные зависимости u, i, p емкостного элемента: а – емкостный элемент; б – зависимости i(t), u(t), p(t)

Мгновенная мощность, поступающая в емкостный элемент, имеет тот же характер, что и в случае индуктивного элемента:

При этом средняя мощность за период в емкостном элементе равна нулю. Энергия, связанная с электрическим полем емкостного элемента определяется: