16.13. Преобразования Лапласа

Линейные дифференциальные уравнения с постоянными коэффициентами могут быть решены с помощью интегральных преобразований Лапласа. Раз­личным функциям действительных переменных (времени t) эти преобразования соответствуют функции комплексной переменной p = α + jω и наоборот. Ком­плексную переменную необходимо отличать от переменной , которая обозна­чает оператор дифференцирования.

Прямое преобразование Лапласа функции времени f(t) определяется соотно­шением

.

(16.105)

Функциюf(t) называют оригиналом, а F(p) – изображением функции f(t) по Лапласу. Таким образом, можно записать:

т.е. оригинал соответствует изображению.

Запишем некоторые изображения, которые доказываются в курсе высшей мате­матики:

изображение постоянной величины

изображение производной функции f(t)

изображение интеграла функции f(t)

16.14. Законы Ома и Кирхгофа в операторной форме

Пусть цепь (рис.16.21) подключается к источнику напряжения при ненуле­вых начальных условиях, т.е. до коммутации в цепи проходил некоторый ток. То­гда можем записать:

i(0) ≠ 0,

uC ≠ 0.

Составим дифференциальное уравнение переходного процесса:

,

(16.110)

где

.

(16.111)

Заменим оригиналы функций их изображениями по Лапласу (рис.16.22):

Тогда получим:

.

Отсюда

.

(16.112)

Полученное уравнение подобно закону Ома в операторной форме для пере­ходного процесса при ненулевых начальных условиях.

В знаменателе находится операторное сопротивление

.

(16.113)

Оно может быть определено из комплекса полного сопротивления синусои­дального тока

путём замены jω на p.

При нулевых начальных условиях, т.е. при i(0) = 0 и u_C(0) = 0, получим:

.

(16.114)

Аналогично можно записать законы Кирхгофа в операторной форме:

;	(16.115)
.	(16.116)

16.15. Теорема разложения

В большинстве случаев изображения представляют собой полную рациональ­ную дробь:

,

(16.117)

в которой m < n, a_k и b_k – действительные числа, p₁, p₂, … p_n – корни урав­нения F(p) = 0, которые не кратны и не равны корням уравнения φ(p) = 0.

Из математики известно, что в этом случае:

= .

(16.118)

Это и есть запись теоремы разложения, которая позволяет с помощью изо­браже­ния в виде рациональной дроби найти оригинал, который равен сумме показа­тельных функций времени, умноженных на постоянные коэффициенты.

16.16. Формула включения

Если при расчёте операторным методом на постоянном напряжении искомая величина (ток или напряжение) описывается выражением

,

(16.119)

то переход к оригиналу может быть выполнен с помощью, так называемой фор­мулы включения с нулевыми начальными условиями:

.

(16.120)

Например, необходимо найти закон изменения тока в цепи, изображённой на рис.16.23.

Запишем дифференциальное уравнение:

или

.

Заменим оригиналы их изображениями:

;

,

тогда

.

Чтобы перейти от изображения к оригиналу, применим формулу включения. Находим корень из уравнения:

;

,

откуда

.

Возьмём производную функции F(p) = 0:

.

Записываем оригинал тока:

.

Воспользуемся теперь теоремой разложения:

.

Найдём корень из уравнения:

,

.

Функция F′(p) = r.

Записываем оригинал тока:

.

Чтобы перейти от изображения к оригиналу, можно воспользоваться табличными формулами, для чего нужно преобразовать выражение изображения тока:

= .

Из таблицы находим:

= .

Итак, можем записать:

,

что совпадает с результатами, полученными раньше, и классическим методом рас­чёта.

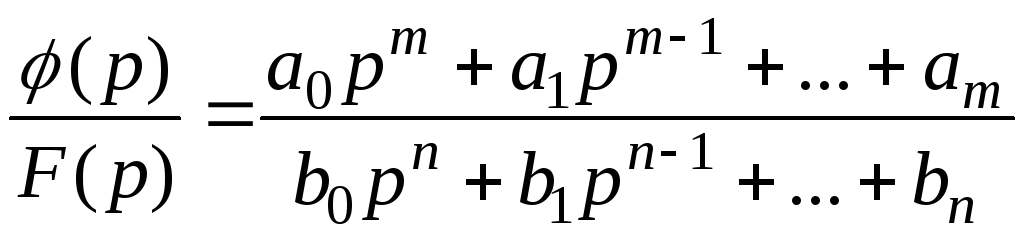27