bmp
.pdfВ.А.Баженов, Г.М.Іванченко, О.В.Шишов, С.О.Пискунов
БУДІВЕЛЬНА МЕХАНІКА
Розрахункові вправи. Задачі. Комп’ютерне тестування
Навчальний посібник
Київ 2013
ЗМІСТ
1. Система сил на площині........................................................... |
5 |
|
1.1. |
Короткі теоретичні відомості .............................................................. |
5 |
1.2. |
Довільна система сил ........................................................................... |
11 |
1.3. |
Задачі для самоконтролю ................................................................... |
16 |
2. Кінематичний аналіз плоских систем і визначення реак- |
17 |
|
цій у в’язях.................................................................................. |
||
2.1. Короткі відомості про кінематичний аналіз ...................................... |
17 |
|
2.2. |
Приклади кінематичного аналізу розрахункових моделей .............. |
27 |
2.3. |
Схеми задач для самостійного розв’язування ................................... |
41 |
3. Розрахунок плоских статично визначуваних ферм ............ |
43 |
3.1. Короткі теоретичні відомості .............................................................. |
43 |
3.2.Приклади визначення внутрішніх зусиль у стержнях простих
|
ферм ....................................................................................................... |
47 |
3.3. |
Схеми задач для самостійного розв’язування ................................... |
53 |
4. Статично визначувані просторові ферми............................. |
54 |
|
4.1. |
Короткі теоретичні відомості ............................................................... |
54 |
4.2. |
Приклад розв’язування просторової ферми ........................................ |
60 |
4.3. |
Задачі для самостійного розв’язання ................................................... |
64 |
5. Розрахунок шарнірно-консольної балки .............................. |
65 |
|
5.1. |
Основні теоретичні відомості ............................................................. |
65 |
5.2. |
Приклад розрахунку шарнірно-консольної балки ............................ |
67 |
5.3. |
Задачі для самостійного розв’язування ............................................. |
71 |
6. Розрахунок тришарнірних арок.............................................. |
72 |
|
6.1. |
Короткі теоретичні відомості ............................................................. |
72 |
6.2. |
Приклади визначення внутрішніх зусиль ......................................... |
75 |
6.3. |
Схеми задач для самостійного розв’язування.................................... |
85 |
7. Статично визначувані рами..................................................... |
86 |
|
7.1. |
Основні теоретичні відомості ............................................................. |
86 |
7.2. |
Розрахунок простої рами...................................................................... |
89 |
7.3. |
Розрахунок складеної рами ................................................................. |
93 |
7.4. |
Розрахунок рами із замкненим контуром .......................................... |
99 |
7.5. |
Задачі для самостійного розв’язання ................................................. |
103 |
8. Розрахунок на рухоме навантаження ........................................... |
104 |
|
8.1 |
Короткі теоретичні відомості ............................................................... |
104 |
8.2 |
Лінії впливу для двоопорної балки ..................................................... |
104 |
8.3 |
Лінії впливу для консольної балки ...................................................... |
108 |
8.4 |
Навантаження ліній впливу .................................................................. |
110 |
8.5 |
Лінії впливу для шарнірно–консольної балки .................................... |
114 |
8.6 |
Лінії впливу в фермах .......................................................................... |
116 |
8.7 |
Лінії впливу в шпренгельних фермах ................................................. |
123 |
3
8.8 |
Приклади визначення зусиль за допомогою ліній впливу ................ |
132 |
8.9 |
Задачі для самостійного розв’язування .............................................. |
142 |
9. Обчислення переміщень у стержневих системах................. |
143 |
|
9.1. |
Короткі теоретичні відомості ............................................................ |
143 |
9.2. |
Визначення переміщення в рамі ....................................................... |
143 |
9.3. |
Визначення переміщення в фермі ..................................................... |
149 |
9.4. |
Визначення переміщення від дії температури ................................. |
151 |
9.5. |
Визначення переміщення від змушених переміщень опор ............. |
153 |
9.6. |
Задачі для самостійного розв’язування ............................................. |
155 |
10. Розрахунок статично невизначуваної рами методом сил.. |
157 |
|
10.1. |
Короткі теоретичні відомості ......................................................... |
157 |
10.2. |
Розрахунок рами методом сил ........................................................ |
165 |
10.3. |
Розрахунок симетричної рами методом сил .................................. |
172 |
10.4. |
Задачі для самостійного опрацювання ........................................... |
178 |
11. Статично невизначувані ферми.............................................. |
179 |
|
11.1. |
Короткі теоретичні відомості ........................................................... |
179 |
11.2. |
Приклад розрахунку ........................................................................ |
184 |
11.3. Задачі для самостійного опрацювання............................................ |
194 |
|
12. Нерозрізна балка ....................................................................... |
195 |
|
12.1 |
Основні теоретичні відомості ......................................................... |
195 |
12.2Розрахунок статично невизначуваної балки на постійне наван-
таження методом трьох моментів .................................................. |
202 |
12.3Розрахунок нерозрізної балки на тимчасові навантаження мето-
|
дом моментних фокусів ................................................................... |
206 |
12.4 |
Побудова ліній впливу...................................................................... |
217 |
12.5 |
Задачі для самостійного опрацювання ........................................... |
225 |
13. Метод переміщень ..................................................................... |
225 |
|
13.1. |
Короткі відомості про метод переміщень ...................................... |
225 |
13.2. |
Розрахунок несиметричної рами в канонічній формі .................... |
233 |
13.3. |
Розрахунок несиметричної рами в розгорнутій формі .................. |
242 |
13.4. |
Розрахунок симетричної рами на симетричне навантаження ....... |
246 |
13.5. |
Розрахунок симетричної рами в розгорнутій формі ...................... |
256 |
13.6. |
Задачі для самостійного опрацювання ........................................... |
263 |
14. Метод скінченних елементів для стержневих систем ........ |
264 |
|
14.1. |
Основні положення методу скінченних елементів ....................... |
264 |
14.2. |
Приклад розрахунку плоскої рами ................................................. |
278 |
14.3.Приклад розв’язування просторової рами методом
скінченних елементів. ...................................................................... |
291 |
14.4.Приклад розв’язування статично невизначуваної шарнірно-
|
стержневої системи методом скінченних елементів ..................... |
308 |
14.5. Схеми для самостійного розв’язування ......................................... |
318 |
|
15. Розрахунок рам на стійкість ................................................... |
319 |
|
15.1. |
Короткі теоретичні відомості ......................................................... |
319 |
15.2. Приклад розрахунку рами на стійкість .......................................... |
324 |
|
15.3. Розрахунок на стійкість симетричної рами ................................... |
339 |
|
15.4. Задачі для самостійного розв’язування .......................................... |
347 |
|
16. Динамічний розрахунок рам ................................................... |
348 |
|
16.1. |
Короткі відомості про розрахунок на динамічні дії ..................... |
348 |
16.2. |
Приклад динамічного розрахунку рами .......................................... |
354 |
16.3.Виконання розрахунково-графічної роботи з використанням
комп’ютерної програми ................................................................... |
370 |
16.4. Задачі для самостійного опрацювання ........................................... |
372 |
4
17. Навчальний програмний комплекс АСИСТЕНТ............... |
373 |
17.1.Основні характеристики……………………………………………. 373
17.2. |
Запуск комплексу АСИСТЕНТ………………………………….. |
374 |
17.3. |
Керування роботою комплексу………………………………….… |
374 |
17.4.Виконання розрахункових робіт………………………………….. 375
17.5. Статичні та динамічні розрахунки стержневих систем…………. 378
18. Обчислювальний комплекс Structure CAD.......................... |
386 |
|
18.1. |
Основні характеристики |
386 |
18.2. |
Установлення ОК SCAD |
389 |
18.3. Завантаження ОК SCAD і основні елементи керування |
390 |
|
18.4. Основні етапи створення розрахункової схеми в ОК SCAD |
397 |
|
18.5. Виконання розрахунку в ОК SCAD |
426 |
|
18.6. |
Перегляд і документування результатів |
429 |
Додатки ....................................................................................... |
434 |
|
Література ................................................................................... |
440 |
|
1. Система сил на площині
1.1.Короткі теоретичні відомості
Сила – це фізична величина, яка визначає кількісну міру механічної взаємодії тіл. Сукупність сил, що діють на тіло, називається системою сил. Дія сил обумовлює механічний стан тіла, зміну з часом його положення у просторі відносно інших тіл та зміну його форми. Одиницею виміру сили в Міжнародній системі СІ є ньютон – 1Н. Це досить мала величина для використання в інженерних розрахунках у будівельній справі. Зручніше працювати з тисячами ньютон (кілоньютон) 1кН=103Н та мільйонами ньютон (меганьютон) 1мН=106Н.
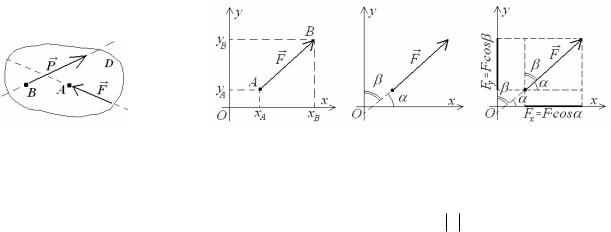
Сила є векторною величиною. На площині її визначають декілька параметрів: абсолютна величина (модуль), напрямок та лінія дії. При вивченні деформацій тіл важливо знати також точку прикладання сили. Ідеалізовані тіла, які міняють свою форму лише за рахунок деформацій, називатимемо дисками. Сила на схемах і в текстах розрахунків позначається великою латинською літерою зі стрілочкою зверху. При потребі літерні позначення сил використовуються з нижніми цифровими індексами. Графічно вектор сили зображається відрізком зі стрілкою, спрямованою в бік дії сили. Такий відрізок у багатьох випадках має бути пов’язаним з точкою прикладання сили, наприклад сили F та P , які діють в точках А і В на диск D (рис.1.1).
а |
б |
в |
Рис.1.1 |
Рис.1.2 |
|
Довжина відрізка при аналітичному розв’язуванні задач довільна – схематична, а при графіч-
ному повинна в певному масштабі сил дорівнювати модулю сили F F , а напрямок має відпові-
дати напрямку її дії на схемі. Запис T P означає, що дві сили мають однаковий модуль, протилежні напрямки і діють вздовж однієї прямої або паралельних прямих. Аналітичне визначення сили передбачає попередній вибір системи координат, в якій задаються проекції сили на осі (рис. 1.2,а). Проекції вектора ще носять назву "координат вектора". Позначаються проекції вектора тією ж літерою, що й його модуль (але без стрілочки зверху), із назвою осі в нижньому індексі, наприклад Fx , Fy . Вони чисельно дорівнюють різниці координат кінцевої і початкової точок вектора на відповідній осі, проградуйованій в одиницях вимірювання сил. Також вважається що вектор зада-
6
но, якщо відомі його модуль і кути між додатними напрямами осей координат та напрямом вектора сили – направляючі кути (рис.1.2,б). На практиці проекцією сили на вісь визначатимемо як добуток модуля сили на косинус направляючого кута до відповідної осі (рис.1.2,в). Слід мати на увазі, що косинус прямого кута дорівнює нулю, а тупого кута – від’ємний. Тому проекція сили на вісь також може мати нульове значення (якщо лінія дії вектора сили перпендикулярна до цієї осі) або бути меншою за нуль.
Розділ механіки, в якому вивчаються загальні положення про сили та умови рівноваги тіл називається статикою. Під рівновагою розуміють стан спокою тіла по відношенню до інших тіл (відсутність прискорень у нерухомій системі координат). У статиці розглядають дві основні задачі: приведення системи сил, що діє на тіло, до найпростішого вигляду та визначення умов рівноваги сил. Тіла можуть бути вільними, переміщенню яких ніщо не перешкоджає. Ідеалізовані пристрої та інші тіла, які утримують тіло, механічний стан якого вивчається, від певних переміщень (кутових або лінійних) називаються в’язями, а саме тіло – не вільним. Сили взаємодії тіл, що виникають у в’язях, називаються реакціями.
В основі статики лежить низка аксіом, які узагальнюють життєвий досвід, численні експерименти та спостереження за рівновагою і рухом тіл.
Аксіома 1. Вільне абсолютно тверде тіло під дією двох сил може знаходитись у рівновазі лише тоді, коли ці сили мають однакові модулі, діють вздовж однієї прямої і мають протилежні напрями F P (рис.1.3). Така система сил є зрівноваженою.
Рис.1.3 |
Рис.1.4 |
Під дією однієї сили тіло не може бути у рівновазі.
Аксіома 2. Дія заданої системи сил на абсолютно тверде тіло не зміниться, якщо до неї добавити або від неї забрати зрівноважену системусил (рис.1.4).
Не змінюючи механічного стану тіла силу можна переносити вздовж лінії дії.
7
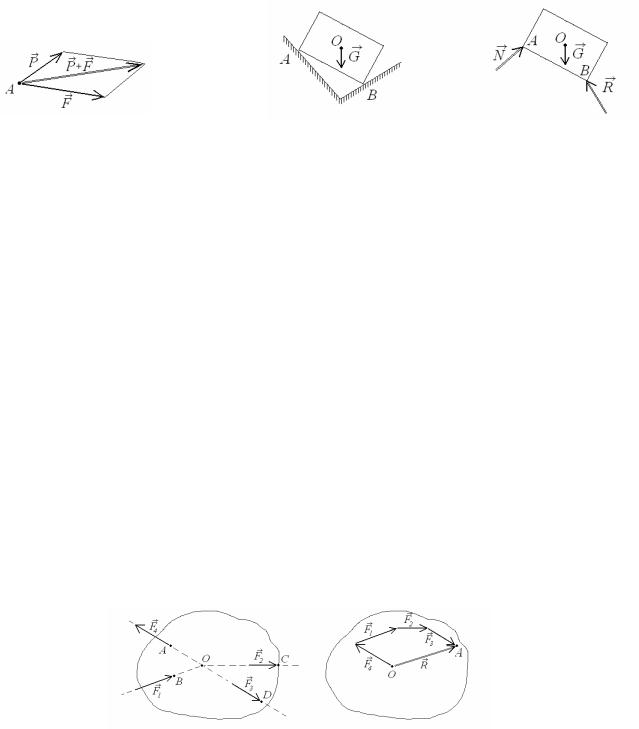
Аксіома 3. Система двох сил, прикладених до точки А, має рівнодійну, яка зображується діагоналлю паралелограма, побудованого на цих силах і має початок у точці А (рис.1.5).
а |
б |
Рис.1.5 |
Рис.1.6 |
Ця аксіома ще називається додаванням векторів за правилом паралелограма. Вектори-доданки називатимемо компонентами вектора-суми.
Аксіома 4. Сили взаємодії двох матеріальних тіл завжди рівні за модулем і протилежні за на-
прямом – дії завжди відповідає рівна і протилежна протидія.
Аксіома 5. Рівновага тіла, що може деформуватись, не порушиться, якщо тіло вважати абсолютно твердим.
Аксіома 6. Не вільне матеріальне тіло можна розглядати як вільне, якщо всі в’язі замінити реакціями в них (рис.1.6).
Залежно від взаємного розміщення сил на площині система сил може бути збіжною або довільною.
Збіжна система сил
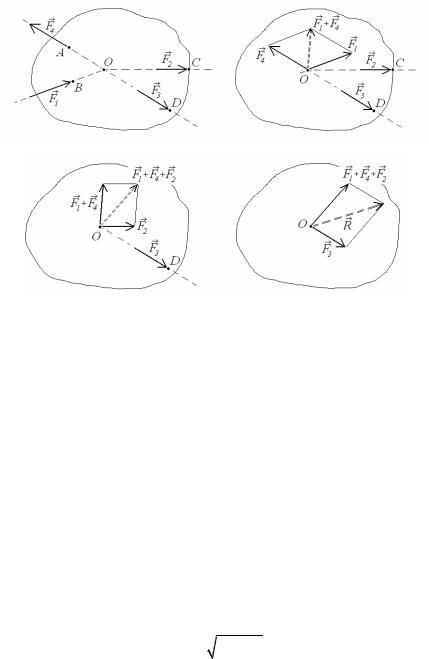
Збіжною називається система сил, лінії дії яких перетинаються в одній точці (рис.1.7). Така система приводиться до однієї сили, яка носить назву рівнодійної (еквівалентної) – сили, дія якої на абсолютно тверде тіло така ж, як і вихідної системи. Лінія дії рівнодійної сили також проходить через точку перетину всіх сил системи.
Рис. 1.7 |
Рис.1.8 |
Графічно для пошуку вектора рівнодійної сили потрібно визначити геометричну суму векторів всіх сил-доданків. Для цього можна скористатись правилом трикутника (багатокутника) і створити ланцюжок вишикуваних в будь-якій послідовності сил, перша і остання точки якого визначають шуканий вектор (рис.1.8). Причому, початок цього вектора співпадає з першою точкою силового
8
ланцюжка – точкою О, а закінчення – з останньою – точкою А. Також можна декілька разів скористатись правилом паралелограма, додавши спочатку будь-які дві сили із системи і далі послідовно додавати до отриманого вектора-суми чергову силу (рис.1.9 а-г). Графічне розв’язування будь-якої задачі потрібно виконувати в оптимальному масштабі. Дрібні зображення приводять до втрати точності результату.
а |
б |
в |
г |
Рис. 1.9
Аналітичний пошук рівнодійного вектора збіжної системи сил полягає у визначенні проекцій шуканого вектора на осі вибраної системи координат (зручніше працювати в прямокутній декартовій системі – системі координат з однаковими довжинами базисних векторів) з подальшим обчисленням модуля рівнодійного вектора та його направляючих кутів. Проекції рівнодійної n сил на осі декартової системи координат дорівнюють сумі проекцій усіх сил системи на ці осі:
Rx n |
Pi cos i , |
Ry n |
Pi cos i , |
(1.1) |
i 1 |
|
i 1 |
|
|
де Rx, Ry – проекції вектора рівнодійної сили на осі системи координат, i, i– кути між напрямами вектора сили Pi і осями Оx та Оу відповідно.
Модуль вектора рівнодійної у прямокутній системі координат визначається співвідношенням
|
|
|
|
|
|
|
|
|
|
|
|
R R2 |
R2 |
, |
|
|
(1.2) |
||
|
|
|
|
x |
y |
|
|
|
|
а величини направляючих кутів |
|
|
|
|
|
|
|
|
|
arccos |
R |
x |
, |
arccos |
Ry |
. |
(1.3) |
||
|
|
R |
|||||||
|
R |
|
|
|
|
||||
У достовірності результатів розв’язування задачі можна впевнитись після порівняння відповідей, отриманих аналітично і графічно. Для цього слід вимірюванням визначити проекції графічно
9
отриманого вектора рівнодійної сили на осі прийнятої системи координат Rx та Ry та його направляючі кути.
Відносна похибка графічних результатів (аналітичні, очевидно, більш точні) визначається за формулою
|
Пан Пгр |
100% , |
(1.4) |
|
|||
|
Пан |
|
|
де Пан, Пгр– величини параметру, визначені аналітично і графічно.
Величина відносної похибки залежить не лише від якості розрахунку, а й від співвідношення величини, що перевіряється, до інших. Точність малих величин, визначених графічно, як правило, менша.
Приклад 1.
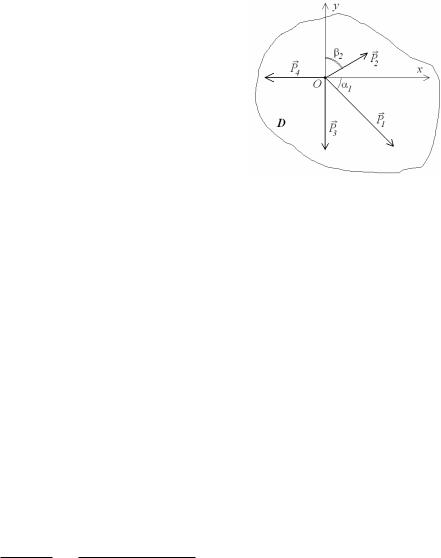
Дано: абсолютно тверде тіло D, збіжна система сил P1, P2 , P3 , P4
(рис.1.10):
P1 = 40 кН, P2 =20 кН, P3 =30 кН, P4 =25 кН,1 =45о, 2 =60о.
Рис. 1.10
Необхідно: привести систему сил до рівнодійної сили аналітично та графічно, порівняти результати.
Аналітичне розв’язування
Проекції вектора рівнодійної на осі системи координат Oxy:
Rx 4 Pix P1x P2x P3x P4x 40 cos 45 20 cos30 30 cos90 25 cos180
i 1
40 0,7071 20 0,8660 30 0 25 1 20,60 кН;
Ry 4 Piy P1y P2 y P3y P4 y 40 cos135 20 cos60 30 cos180 25 cos90
i1
40 0,7071 20 0,5 30 1 25 0 48,28кН.
Модуль вектора рівнодійної сили:
R 
Rx2 Ry2 
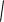20,602 48,28 2 52,49 кН.
Напрямні кути вектора рівнодійної сили:
10
arccos RRx arccos 5220,,6049 arccos0,3925 66,89 ;
arccos RRy arccos 5248,49,28 arccos 0,9198 156,89 .
Графічне розв’язування
Порівняння результатів розв’язування двома способами наведено в табл.1.1 :
|
|
|
|
Таблиця 1.1. |
Параметр |
Графічний |
Аналітичний |
Відносна |
|
|
|
|
||
|
|
спосіб |
спосіб |
похибка (%) |
|
|
|
|
|
Rx (кН) |
20,5 |
20,60 |
0,5 |
|
|
|
|
|
|
Ry (кН) |
- 48,5 |
- 48,28 |
0,5 |
|
|
|
|
|
|
R (кН) |
52,5 |
52,49 |
0,1 |
|
|
|
|
|
|
|
(град.) |
67 |
66,89 |
0,2 |
|
|
|
|
|
|
(град.) |
157 |
156,89 |
0,1 |
|
|
|
|
|