10.2.1.3. Метод главного критерия

Суть метода состоит в том, что ЛПР выделяет главный критерий (далее f₁(X)), а на остальные критерии накладывает требования, что они были не меньше задаваемых им минимальных (пороговых) значений t_i. Тогда многокритериальная задача сводится к однокритериальной задаче

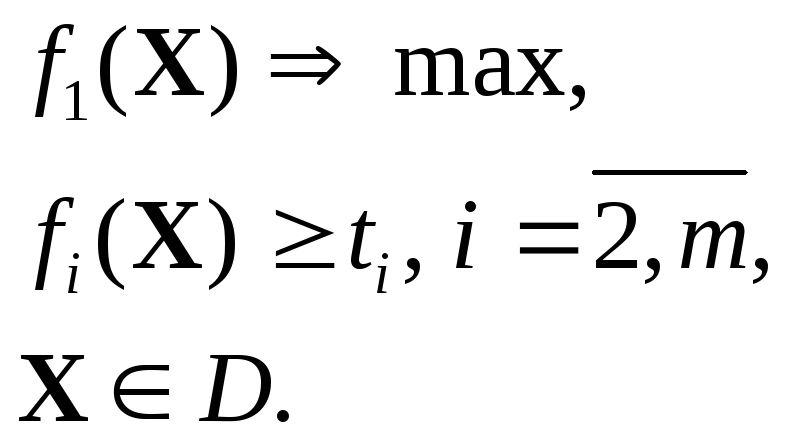(10.16)

Если эта задача разрешима, то ее решение всегда является слабо эффективным, а если оно единственно, то и эффективным. Заметим, что этот вывод не зависит от выбора главного критерия. Рис.10.7 иллюстрирует случай единственного решения задачи (10.16), а рис.10.8 – множества оптимальных решений, лежащего на границеab, из которого только точка а является эффективной.

Практически задачу (10.16) решают для нескольких наборов значений {t_i}, и затем на основании анализа полученных (слабо) эффективных решений ЛПР определяет наиболее предпочтительное из них.

Рассмотренный метод целесообразно применять, когда ЛПР может обоснованно назначить значенияt_i или указать узкие пределы для них.

10.2.1.4. Линейная свертка

Если ЛПР может не только ранжировать критерии, но и дать сравнительную количественную оценку значимости (важности) критериев, решение многокритериальной задачи сводится к обычной задаче с одним критерием, в качестве которого берется обобщенный показатель вида

, (10.17)

где С_i- положительные числа, отражающие веса критериев в структуре предпочтений ЛПР. При групповом ЛПРC_i находятся по индивидуальным весам одним из методов обработки экспертных оценок. Обычно значенияС_iнормируются так, чтобы=1. Как следует из теоремы 5, точка максимума функции (10.17) при положительныхС_iявляется эффективной.

Данный способ решения многокритериальной задачи имеет существенные недостатки. Во-первых, большие затруднения возникают при определении весов. Одно дело – расположить критерии по важности, и совсем другое - оценить на сколько или во сколько один критерий важнее другого. Во-вторых, неизвестна связь между значениями весов и значениями критериев в точке максимумаF(Х).Очень часто эта зависимость оказывается существенно нелинейной (даже в линейных задачах), включая зоны нечувствительности значенийf_i к изменениюC_i. Поэтому для получения решения, удовлетворяющего ЛПР, приходится максимизироватьF(X) для нескольких наборовС_i. Наконец, заметим, что в свертке (10.17) целесообразно все критерии приводить к одним единицам измерения. С этой целью лучше представлять критерии в относительных единицах, беря за базовое максимальное или желаемое значение. Достоинство метода – в стандартности задачи, к которой сводится исходная многокритериальная проблема.

Пример 10.1. Рассмотрим задачу линейного программирования с тремя критериями: максимизировать

f₁(X)=-3x₁+ 2x₂,

f₂(X) = 4x₁₊ 3x_2,

f₃(X)=2x₁-5х₂

при условиях

2x₁+3x₂18,

2x₁+x₂10,

x₁,x₂0.

Допустимая область и линии равного уровня критериев показаны на рис.10.9. Максимальное значение функции f₁(X) равно 12 и достигается в точке А(0,6), при этом=18,=-30;max f₂(X)=24 в точке В(3,4), где=-1 и=-14; mахf₃(Х)=10 в точке С(5,0),в которой=-15 и=20. Если взять свертку с равными весами, то есть

то результат максимизации F(Х), как легко убедиться, совпадает с максимизацией одной функцииf₃(Х). Таким образом, при равных весах решение по линейной свертке дает наилучшее значениеf₃и наихудшее дляf₁. Используя параметрическое программи­рование,можно определить диапазон значенийC_i (зону нечувствительности), в котором оптимальное решение по F(Х) будет оставаться в точке С.