10.2.3. Построение эффективного множества

Очевидно, что если ЛПР показать эффективное множество в целом, то он сам сможет выбрать тот эффективный вектор, который предпочитает всем остальным. В таком случае для решения задачи не потребуется извлекать знания о предпочтениях ЛПР. Этот подход особенно удобен, если имеет место групповое принятие решений. Однако при числе критериев свыше двух построение эффективного множества оказывается непростой задачей. Дело не только в невозможности многомерного представления всего множества, но и в том, что даже для линейных задач эффективное множество является невыпуклым (часть границы выпуклого многогранного множества).

Рассмотрим кратко некоторые способы построения эффективных множеств. Для линейных многокритериальных задач эффективное множество векторов критериев полностью определяется входящими в него вершинами множества достижимостиG(для множества эффективных решений – эффективными вершинамиD). Применяя один из методов свертки с весами и решая задачу с разными ненулевыми значениями весов (построив сетку весов или параметрически), можно найти многие (реже – все) эффективные вершины. Заметим, что линейная свертка дает только вершины, другие способы свертки могут давать эффективные точки на ребре или грани. Чтобы получить представление о всем эффективном множестве, следует после нахождения очередного оптимального (эффективного) решения найти все альтернативные оптимальные решения, которые существуют, если среди оценок небазисных переменных есть нулевые (вводя поочередно эти переменные в базисное решение, можно получит все вершины эффективной грани). Подробно и наглядно эти вопросы рассмотрены в книге Р. Штойера[35]. При воссоздании эффективного множества по вершинам нужно помнить, что из-за его невыпуклости не всякая выпуклая комбинация эффективных вершин дает эффективную точку. Так как на рис.10.24 выпуклая комбинация эффективных вершин порождает треугольникABC, хотя эффективными являются только его стороныAB и BC. Для наглядности представления эффективное множество линейной задачи можно проектировать на плоскость – оно будет иметь вид одного или нескольких многоугольников с общими ребрами и вершинами (как развертка трехмерной фигуры). У каждой вершины может быть выведен соответствующий критериальный вектор. Выбор наилучшего решения облегчится, если ЛПР, перемещая указатель по представленному эффективному множеству, будет получать значения критериального вектора в точке указателя или иное представление, например, в виде графиков, о поведении вектора.

В отличие от описанного способа метод ограничений может применяться как для линейных, так и нелинейных многокритериальных задач. В критериальном пространстве строится сетка, значения критериев в узлах которой выступают в качестве ограничений на соответствующие критерии. Для этого сначала решается m однокритериальных задач (на максимум каждого частного критерия), которые дают диапазоны изменения каждого критерия [] на эффективном множестве. Сетка, накладываемая на этот интервал, включает S+1 узел:

. (10.39)

Затем для каждого критерия решаются задачи:

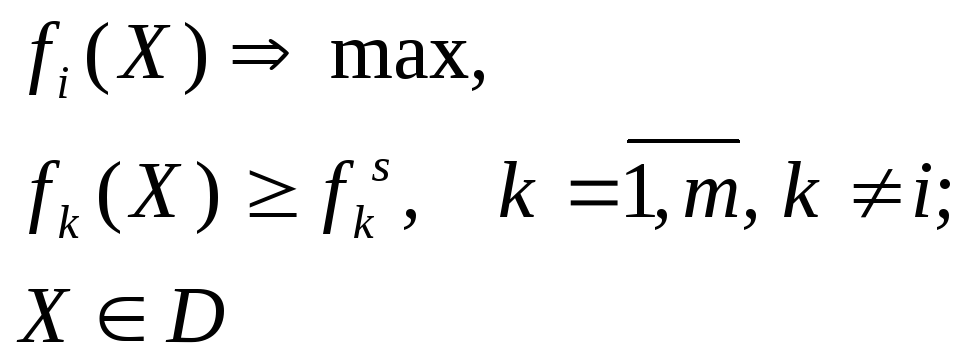(10.40)

для всех возможных сочетаний из (10.39). Чем мельче сетка, тем точнее можно представить эффективное множество (рис.10.25). Основным недостатком данного метода является большое число решаемых задач (10.40). При этом часть из них может оказаться неразрешимой, а часть может дать лишь слабо эффективные точки.

Так как не все процедуры гарантируют получение эффективных решений, для проверки эффективности следует использовать условия оптимальности, рассмотренные в разделе 10.1.4. Если решение удовлетворяет необходимым условиям, то гарантировать его эффективность нельзя. Но если оно не выполняется, то решение однозначно не эффективно. Удовлетворение достаточ­ных условий гарантирует эффективность решения. В противном случае ничего определенного об эффективности решения сказать нельзя. Наконец решение всегда эффективно, если оно удовлетворяет как необходимым, так и достаточным условиям.

В задачах с выпуклым множеством D допустимых решений и линейными критериями множество достижимости G выпукло. В таких случаях легче построить все множество G, чем невыпуклое эффективное множество. В то же время G дает полное представление о структуре последнего. Это преимущество особенно проявляется в линейных многокритериальных задачах, т.к. многогранное выпуклое множество G можно описать в виде

(10.41)

удобном для его построения. Имея G, легко получить любое двумерное сечение, необходимое ЛПР, или его проекции, которые выводятся на экран, обеспечивая более полное представление обо всем множестве достижимости и о его эффективном подмножестве. Можно также использовать аппроксимацию G более простой геометрической фигурой, имеющей ту же эффективную границу, что и G.

Для построения множества G в виде (10.41) применяют теорию линейных неравенств. Рассмотрим неравенство

, (10.42)

в котором v и w – k и l-мерные векторы переменных. Очевидно, что система (10.42) порождает в (k+l)-мерном пространстве некоторое многогранное множество M. Построим на нем множество M_w таких точек w’E¹, что для каждой найдется хотя бы одна точка v’ E^k, образующая пару {v’,w’}, удовлетворяющую (10.42). Поясним построение М_w на примере простой системы с k=l=1:

1),2),3),

4),5),6).

Множество M_wполучим, если исключим переменную v, для чего следует сложить пары неравенств с противоположными знаками приv(предварительно неравенство делится на коэффициент приv). B результате этих преобразований имеем:

1)+2): ,1)+5): ,2)+4): ,2)+6): ,

3),4)+5): ,5)+6):

Совместное решение неравенств и дает множество M_w:

,

которое представляет собой отрезок осиw (рис.10.26), то есть ортогональную проекцию M на пространство E¹ (здесь E¹). Этот метод может быть улучшен путем использования процедуры фильтрации несущественных ограни­чений в описании M_w.

Применительно к линейной задаче с n переменными и m критериями многогранное множество в пространстве E^n+m представляется в виде

.

Очевидно, что интересующее нас множествоG (аналог M_w) является ортогональной проекцией Z на критериальное пространство Е^m и может быть построено рассмотренным методом. Как отмечалось выше, в сложных случаях вместо точного множества G легче представить его аппроксимацию, но при этом упрощенное множество должно иметь то же эффективное множество, что и G. Более подробное рассмотрение этих вопросов выходит за рамки конспекта. В качестве иллюстрации на рис.10.27 показаны двумерные сечения (проекции) множества G для задачи с 4 критериями.

Другой способ построения сечений связан с понятием оболочки Эджворта-Парето (ОЭП). Под ОЭП понимается множество достижимостиG вместе со всеми доминируемыми им точками критериального пространства. Из определения следует, что множества Парето на G и ОЭП совпадают. Пример ОЭП для задачи ЛП с двумя критериями приведен на рис. 10.28. ЛПР предъявляются сечения не множества G, а оболочки Эджворта-Парето. В [21] показано, что при этом упрощается построение сечений и, что особенно важно, на таких сечениях легче анализировать подмножества Парето.

В практических приложениях методов решения многокритериальных задач редко используется какой-либо один подход в чистом виде, а комбинация подходов позволяет лучше приспособиться к особенностям конкретной проблемы и ЛПР. При этом может оказаться особенно плодотворным сочетание интерактивных процедур и методов представления достижимого (эффективного) множества с использованием средств мультимедиа.

97