10.1.4. Условия оптимальности

Здесь рассмотрим наиболее важные с точки зрения приложений необходимые и достаточные условия оптимальности. Они позволяют строить методы отыскания эффективных решений и способы проверки эффективности найденных решений.

Наиболее общий случай необходимых условий содержит следующая теорема.

Теорема 1. Пусть Y*Gи все . Вектор Y* слабо эффективен тогда и только тогда, когда найдутся такие числа, что

(10.1)

Условие не ограничивает применимость теоремы, так как его всегда можно обеспечить добавлением кположительной константы.

При оговариваемых свойствах D и f(X) справедливы теоремы 2 и 3.

Теорема 2. Пусть D выпукло, а , вогнуты и положительны наD. Тогда решение X* слабо эффективно в том и только в том случае, если существуют такие числа , что

. (10.2)

Теорема 3. Пусть D выпукло, а f вогнуто. Для слабой эффективности точки X^*D необходимо и достаточно, чтобы существовали числа , при которых

. (10.3)

Требование вогнутостиf существенно, так как его невыполнение может привести к тому, что не для всех слабо эффективных решений найдутся, удовлетворяющие (10.3). Например, для критериев и( выпукла) наD=[0,1] множество S(X)=D. Максимум функциидостигается только на одном из концов интервала[0,1] и поэтому ни при каких неотрицательныхимаксимизация этой функции не даст слабо оптимальную точку, лежащую внутриD.

Терема 4.ВекторY^*G эффективен тогда и только тогда, когда для каждого

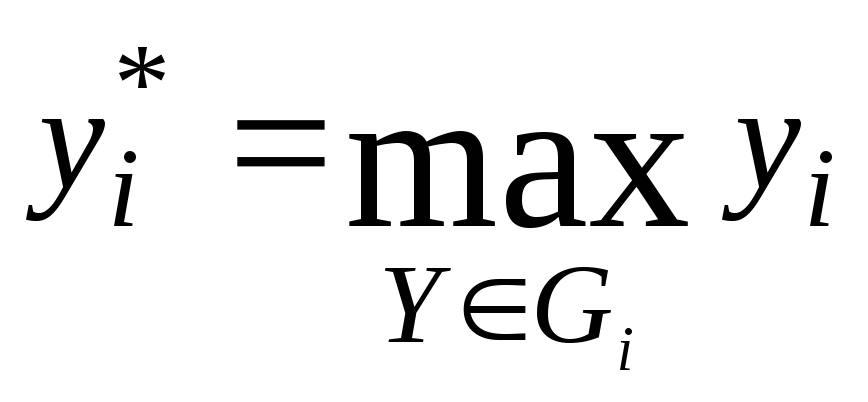, (10.4)

где

¦>, }. (10.5)

Если Y^*G эффективна, то она является единственной вG точкой, удовлетворяющей (10.4) при каждом.

Достаточные условия, приведенные ниже, основаны на свойствах возрастающей функции многих переменных. Поэтому сначала дадим определение такой функции. Числовая функция F(Y), определённая на множествеG, является возрастающей по отношению, если из выполнения неравенстваYY^ для векторовY,Y^G всегда следует справедливость неравенстваF(Y)>F(Y^). Аналогично,F(Y) – функция, возрастающая по отношению >, если изY>Y ^ всегда следуетF(Y)>F(Y^).

Теорема 5.Пусть функцияF(Y) определена на множествеG. Для того чтобы точкаY^*Gбыла эффективной (слабо эффективной), достаточно, чтобы она являлась точкой максимума на множествеG функцииF(Y), возрастающей по отношению(по отношению>).

Теорема легко доказывается от противного. Пусть Y^*G и

F(Y^*)F(Y) для всехYG. (10.6)

Предположим противное, т.е. что существует Y^G, для которого верно неравенствоY ^Y^*. Так как функцияF возрастающая по отношению, то противоречит (10.6). Аналогично доказываются достаточные условия слабой эффективности.

Теорема 5 играет важную роль в решении многокритериальных задач. Её применение основано на максимизации возрастающих функций многих переменных. Поэтому целесообразно рассмотреть примеры таких функций.

1). Функция F(Y)=,где, является возрастающей по каждой переменнойна числовой оси и потому возрастает понаE^m.Поэтому любая точка максимумаF(Y) наGэффективна. Эта же функция прии хотя бы одном из них положительном является возрастающей по отношению> и, значит, максимизация такой функции наG дает слабо эффективную точку.

2

m

m

m

). ФункцияF(Y)=,приs>0 и>0 является возрастающей по каждой переменной на множестве неотрицательных чисел и потому возрастает понаE_{>= (}т.е. в пространств Е где все >=0). Если жеs<0 и>0, то эта функция возрастает по ≥ на Е_> (т.е. в области положительных). Точка максимума такой функции эффективна.

3).Функция F(Y),гдеs>0, >0,а>= ,, возрастает по ≥ наG.Поэтому любая её точка максимума наG эффективна. Отсюда, в частности, следует, что минимизация широко применяемой функциидает эффективную точку.

4

m

m

). ФункцияF(Y) при >0 возрастает по каждой переменнойна множестве положительных чисел и поэтому является возрастающей по ≥ на Е_>. Если же ≥0 и есть среди них положительные, то эта функция будет возрастающей по отношению>на Е_>.

5). Возьмём функцию F(Y) при,. Еслидля всехi, то идля всехi. Поэтому справедливо неравенство

m

и, значит, приведённая функция возрастает по отношению > наE . Следовательно, любая её точка максимума наG слабо эффективна.