10.1.3. Определения

Для описания предпочтений используют бинарные отношения, вводимые на множестве А сравниваемых объектов. В многокритериальной задаче роль таких объектов играют X илиY на множествахD иG соответственно.

Если из двух объектов a и b ЛПР выбираетa, то говорят, чтоaпредпочтительнееb. Все пары вида (a,b), гдеa,bА, для которых a предпочтительнееb, образуют множество, называемое отношением строгого предпочтения наА. Такое отношение обозначают символом(ab или aPb, где Р – первая буква английского словаpreferance – предпочтение).

Объекты a и bнеразличимы для ЛПР, если они одинаковы по предпочтительности. Это значит, что не выполняется ни отношениеab, ниba. Множество всех неразличимых пар(a,b) называют отношением неразличимости или безразличия и обозначают символом ~ (a~b илиaIb, где I происходит от indifference – безразличие).

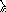
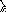
О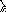чевидно, что для любой парыa,bA выполняется только одно из трех соотношений: ab, ba, a~b. Объединение Pи I дает отношение нестрогого предпочтения, обозначаемого символом (a b или aRb). Отношение a b означает, что a не менее предпочтительно, чем b.

В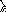соответствии с этими определениями решение Х*D (вектор Y*G) называют оптимальным по отношениюна множествеD (G), если не существует другого решения ХD (вектора YG), для которого справедливо соотношение ХХ* (YY*). Если для любыхXD (YG) выполняется соотношение X* X (Y* Y), то X*D (Y*G)называется оптимальным решением (вектором) по отношению .

При сравнении по предпочтительности векторов Y=f(X) наиболее просто сопоставлять те вектора, которые отличаются лишь одной компонентой. Однако в общем случае частные критерииy_i=f_i(X)могут по-разному соотноситься по предпочтительности в зависимости от того , на каких уровнях зафиксированы остальные критерии. Так если вектор (,) предпочтительнее вектора(), а вектор () менее предпочтителен, чем (), то какое из значение первого критерия,или, предпочтительнее сказать нельзя без знания значений остальных критериев. Так, например, чем выше потолок комнаты, тем лучше, но справедливо это до определенных соотношений высоты, ширины и длины комнаты. Чаще, однако, все значения частного критерия можно упорядочить по предпочтению без учета значений других критериев. Такие критерии называют независимыми по предпочтению от остальных. Примерами могут служить прибыль, издержки и т.п.

Задачи, в которых все критерии независимы по предпочтению, а отношением строгого предпочтения Rявляется отношение>=(не меньше) называются многокритериальными задачами максимизации (аналогично при отношении «не больше» – задачами минимизации).

Напомним, что Rвключает (объединяет)P и I. На множестве G (илиD) отношение строгого порядка P задают неравенством YY’ ( т.е. Y Y’ и YY’ ) или Y>Y’ (т.е. для). Наконец, равенство = порождает отношение безразличия.

Вектор (решение), оптимальный по отношению ≥ на множествеG (D), называется эффективным или парето-оптимальным. Значит, векторY^*G является парето-оптимальным (оптимумом Парето), если не существует векторY  G такой, чтоY  Y^*.Множество таких векторов обозначают через Р(Y) и называют множеством Парето (эффективным множеством). Множество эффективных решений обозначают через Р(X).

Вектор, оптимальный по отношению >, называют слабо эффективным, слабо оптимальным по Парето (слабым оптимумом Парето). Значит, векторY^*G слабо парето оптимальный, если не существуетYG такой, чтоY>Y^*.Множество таких векторов называют слабо эффективным и обозначают черезS(Y).Соответствующее множество слабо эффективных решений имеет обозначение S(X).Если вG не найдётсяYY^*,то не существует иY>Y^*. Следовательно, всякий эффективный вектор одновременно является и слабо эффективным, т.е.P(Y)S(Y). АналогичноP(X)  S(X).

Различие эффективного и слабо эффективного множеств хорошо видно на рис.10.3. Множество P(Y) состоит из частей границы множестваG: кривыхbc, de (исключая точкиd и e ) иgh, а S(Y) – из кривойabcde (включая точкуe) и кривойghk. Точкаd не входит вP(Y), т.к. она доминируется точкойc. Точно также точкаeменее предпочтительна, чемg.

Геометрическое определение множеств P(Y) и S(Y) основано на том, что все точки YE^m, для которых выполняется неравенствоYY⁰, образуют ортант (дляm=2 – прямой угол), стороны которого параллельны координатным осям, а вершиной является точка Y⁰.

Поэтому, если весь угол (ортант), построенный на некоторой точке Y*G, расположен вне множества G, то Y* парето-оптимальна. Если кроме вершины Y* пересечение ортанта и G содержит только точки, лежащие на одной из сторон ортанта, то Y* слабо парето-оптимальна, при этом Y*P(Y), т.е. не является эффективной.

Понятие слабой эффективности оказывается полезным и в случае, когда приходится сокращать первоначальный набор критериев. Нередко на первых этапах исследования трудно определить минимально необходимый набор критериев и поэтому начинают с возможно более полного набора. По мере изучения свойств задачи выявляются несущественные критерии, которые исключаются из дальнейшего рассмотрения. В [30] показано, что множество слабо эффективных решений, выделяемое на полном наборе критериев, содержит все исходные решения, эффективные по сокращенному набору критериев.