
ТЭЦ Лекции
.pdf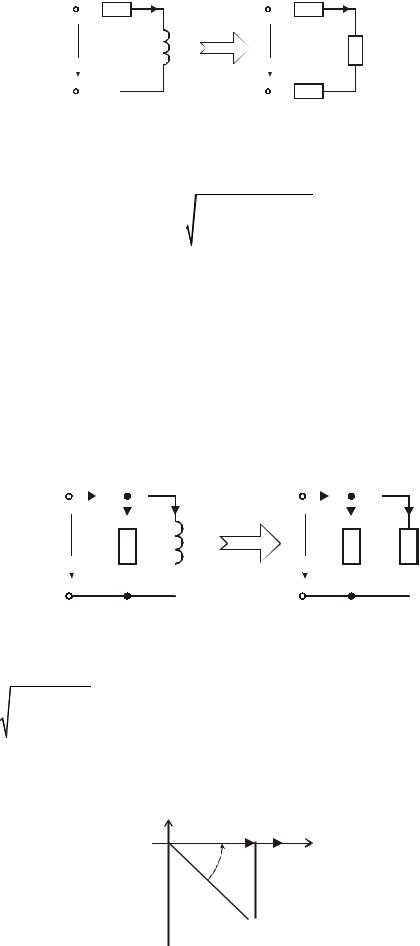
31 /102
|
|
|
|
|
R |
|
i(t) |
|
|
|
|
|
|
R |
|
|
I |
|
|
|
|
|
|
|||||||||
|
|
|
|
u(t) |
|
|
|
L |
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
ZL |
|||||||||
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
ZC |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
На основании II закона Кирхгофа в комплексной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||
U = |
U |
R + U L + |
U |
C |
= R I + Z L I + Z C I = |
R |
+ jω L + |
|
|
|
|
|
I = Z I , где |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jωC |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wL- |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
j×arctg |
wC |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Z = |
R + j ω L |
− |
|
|
= |
R2 + ω L − |
|
|
|
|
|
|
|
e |
|
|
R |
|
|
|
= |
Z |
ejjz . |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
ωC |
|
|
|
ωC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ω L − |
1 |
|
|
|
|
ϕ = ϕz |
= arctg |
ωC |
= arctg |
X |
– фазовый сдвиг между входным напряжением и током. |
||
|
|||||||
R |
|
|
|||||
|
|
|
|
R |
|||
Самостоятельно построить векторную диаграмму на комплексной плоскости!
Анализ параллельно соединенных RL, RC, RLC элементов символическим методом расчёта.
Анализ параллельно соединённых элементов удобно вести с использованием принципа дуальности.
Анализ параллельной RL-цепи.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
комплексная схема замещения |
|
||||||||||||
|
|
|
|
|
|
|
|
|
i(t) |
|
|
|
|
|
|
iL(t) |
|
I |
|
IL |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iG(t) |
|
|
|
IG |
||||||||||
|
|
|
|
|
|
|
|
u(t) |
|
|
|
|
|
|
|
|
|
|
|
U |
YL |
|||||||
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
L |
|
|
|
|
|
G |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании I закона Кирхгофа в комплексной форме: |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
I = I G + I L |
= GU + Y L U = |
G |
+ |
|
|
|
U = Y U , где Y – |
полная комплексная проводимость цепи. |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
j |
ω L |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
1 |
2 |
|
- j×arctg |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
jj |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Y = G − j |
|
= |
G2 + |
|
|
|
|
|
|
|
e |
|
|
|
G wL = |
Y |
e |
|
y , где |
Y |
– |
модуль комплексной проводимости, ϕy – |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
ω L |
|
|
ω L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
аргумент комплексной проводимости. |
|
||||
ϕ = −ϕy = arctg |
1 |
= arctg |
BL |
– фазовый сдвиг между входным напряжением и током. |
|
G ω L |
|
||||
|
|
G |
|
||
|
|
|
|
Im |
IG U Re |
0 ϕ
IL
I 
Из диаграммы видно, что фазовый сдвиг между напряжением и током больше нуля. Вывод: цепь носит индуктивный характер.
32 /102
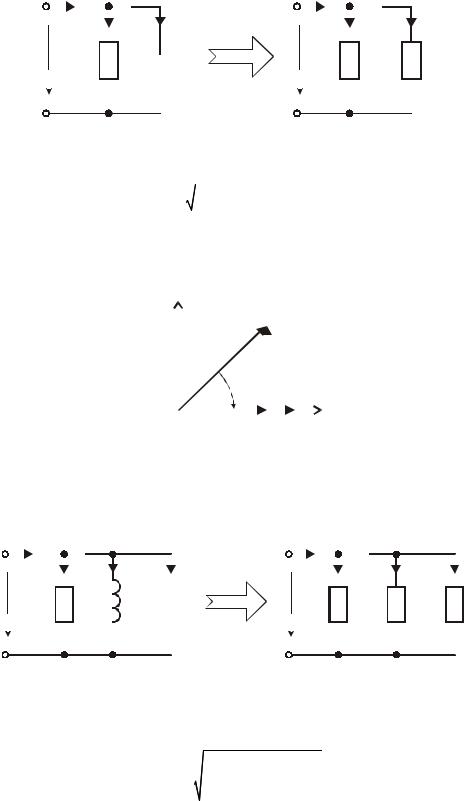
Анализ параллельной RC-цепи. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
комплексная схема замещения |
|
|||||||||||||||
|
|
|
|
|
i(t) |
|
|
iC(t) |
|
I |
|
|
|
|
|
|
IC |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IG |
|||||||
|
|
|
|
|
u(t) |
|
iG(t) |
|
|
|
U |
|
|
|
|
|
YC |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
G |
|
|
|
C |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На основании I закона Кирхгофа в комплексной форме: |
|
|
|
|
|
|
|
|||||||||||||||||||
I = I G + I C = GU + Y C U = (G + jωC ) |
U |
= Y U , где Y – |
полная комплексная проводимость цепи. |
|||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
|
|
|
Y = G + jωC = |
|
j×arctg wC |
= |
|
Y |
|
ejjy , где |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
G2 + (ωC )2 e |
|
G |
|
|
|
||||||||||||||||
|
Y |
|
– модуль комплексной проводимости, ϕy – аргумент комплексной проводимости. |
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
ϕ = −ϕy |
|
= −arctg ωC = −arctg |
BC |
– |
фазовый сдвиг между входным напряжением и током. |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
G |
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Im |
|
|
|
|
|
|
|
|
|
|
|
I |
|
IC |
|
|
|
ϕ |
|
||
|
|
|
Re |
||
|
|
|
|
|
|
0 |
|
|
IG U |
|
|
|
|
||||
Из диаграммы видно, что фазовый сдвиг между напряжением и током меньше нуля. Вывод: цепь носит ёмкостный характер.
Анализ параллельной RLC-цепи.
|
|
комплексная схема замещения |
|
|
||||||
i(t) |
|
|
|
iC(t) |
I |
|
|
IC |
||
|
|
|
|
|
IG |
IL |
||||
|
iG(t) iL(t) |
C |
|
|||||||
u(t) |
U |
G |
YL |
YC |
||||||
|
|
|
|
|
||||||
G |
L |
|
|
|||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
На основании I закона Кирхгофа в комплексной форме:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
I = I G + I L + I C = GU + Y L |
U |
+ Y C |
U |
= G + |
|
|
|
|
+ jωC U = Y |
U |
, где |
|||||||||||||||
|
jω L |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
2 |
1 |
|
2 |
|
j×arctg |
wC - |
wL |
|
|
|
jjy |
|||||||||
|
|
|
|
|
|
|
G |
|
|
|
|||||||||||||||||
|
Y = G + j ωC − |
|
|
= |
|
G + ωC − |
|
e |
|
|
|
|
= |
Y |
e . |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
ω L |
|
|
|
ω L |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ωC − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ = −ϕy |
= −arctg |
ω L |
= −arctg |
B |
– |
фазовый сдвиг между входным напряжением и током. |
|||||||||||||||||||||
|
|||||||||||||||||||||||||||
G |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Самостоятельно построить векторную диаграмму на комплексной плоскости!

33 /102
Мощность в электрической цепи при гармоническом воздействии. Баланс мощности.
|
|
|
|
|
|
|
|
|
|
|
|
i(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u (t ) = Um sin ωt , то есть ϕu |
= 0 . |
|
|
u(t) |
|
|
|
ЛЭЦ |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
i (t ) = Im sin (ωt + ϕi ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ϕ = ϕu |
− ϕi = −ϕi – фазовый сдвиг в цепи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Определим среднюю за период мощность, потребляемой цепью: |
|
|
2 π |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
1 |
|
T |
|
Um Im |
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
|
∫u (t )i (t ) dt = |
|
∫sin ωt sin (ωt − ϕ) dt , с учётом того, что ω = |
|
имеем: |
|
|
||||||||||||||||||||
|
|
|
|
T |
T |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
P = |
Um Im |
cos ϕ = U I cos ϕ . |
|
|
|
|
|
(49) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– активная мощность цепи при гармоническом воздействии [Вт]. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Поскольку полное сопротивление цепи с одной стороны Z = |
U |
, с другой Z = |
|
R |
|
, то U = |
R I |
. |
||||||||||||||||||||||||
|
|
cos ϕ |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
cos ϕ |
||||
|
|
|
|
|
|
|
|
|
P = |
R I |
I cos |
ϕ = R I 2 , |
или P = GU 2 . |
|
|
|
|
|
(50) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
cos ϕ |
|
|
|
|
|
||||||||||||||||||
|
|
|
В ОТЦ вводят понятие реактивной мощности при гармоническом воздействии [ВАр]: |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Q = U I sin ϕ = X I 2 = BU 2 . |
|
|
|
|
|
(51) |
|||||||||||||||
Кроме активной и реактивной мощности используют понятие комплексной мощности [ВА] |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
S = P + jQ = |
|
S |
|
ejϕ . |
|
|
|
|
|
(52) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
= |
|
|
= S полная мощность в цепи, ϕ = arctg |
Q |
– фазовый сдвиг в цепи. |
|
|
|
|
||||||||||||||||||||
|
S |
|
P2 + Q2 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Мощности P, Q и S можно выразить другим способом: |
I e− jϕi |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
S = U I cos ϕ + jU I sin ϕ = U I ejϕ , поскольку ϕ |
u |
= 0 , ϕ = −ϕ , то S =U e j0 |
=U I * . |
(53) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
Таким образом, определяем активную и реактивную мощность: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
P = Re (S ) и Q = Im (S ) . |
|
|
|
|
|
(54) |
|||||||||||||||
Важным понятием в ОТЦ является коэффициент мощности, так как S = U I , а P = U I cos ϕ , то
cos ϕ = |
P |
– |
отношение активной к полной мощности цепи. |
(55) |
|
||||
|
S |
|
|
|
Чем выше cos ϕ , тем |
меньше потерь энергии в линии передачи |
и выше степень |
||
использования электрических машин. Если cos ϕ = 1 , то P = S , Q = 0 . Определим условие выделения максимальной мощности в нагрузке:
|
|
|
|
|
|
|
|
|
Zг |
|
I |
|
|
|
|
|
|
|
|
|
|
Eг |
|
|
|
|
|
|
= Rг + j X г |
|
|
|
Uг |
|
Uн |
|
Zн |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
Z г |
– сопротивление генератора. Z н = Rн + j X н – |
сопротивление нагрузки. |
|||||||||||
I = |
|
|
U |
г |
= |
U г |
|
|
|
|
|||
|
|
|
|
|
|||||||||
|
Z г + Z н |
Rг + Rн + j( X г + X н ) |
. |
|
|
|
|
||||||
Действующее значение тока определяем в виде:
34 /102
I = |
|
I |
|
= |
|
Uг |
, P = U |
|
I = I 2 R = |
Uг2 |
R . |
|
|
|
|||||||||
|
|
|
|
|
(Rг + Rн )2 + ( X г + X н )2 |
||||||
|
|
|
|
|
|
(Rг + Rн )2 + ( X г + X н )2 |
н |
н |
н |
н |
|
|
|
|
|
|
|
Следовательно, максимальная мощность в нагрузке выделяется при условиях:
X |
г |
= − X |
н |
, R = R , то есть Z |
г |
= R − j X |
н |
= Z |
* . |
(56) |
|||
|
|
г н |
|
|
|
н |
|
н |
|
||||
|
|
|
|
P |
= |
Uг2 |
. |
|
|
|
|
(57) |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
нmax |
|
4 Rг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
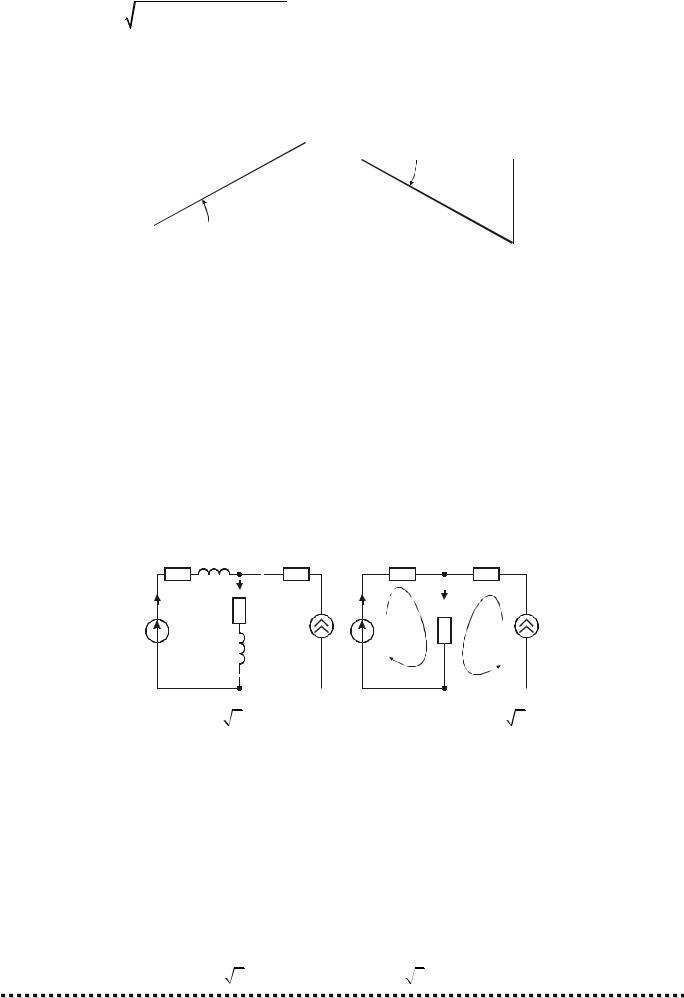
По аналогии с треугольниками сопротивлений и проводимостей введем треугольник мощностей.
|
|
P |
|
S |
|
ϕ |
|
ϕ |
Q |
|
|
|
S |
Q |
|
|
|
|
|
P
В соответствии с законом сохранения энергии развиваемая источниками энергия равна энергии, потребляемой приёмниками.
На основании теоремы Телледжена ∑ S = ∑U I * определим баланс комплексной мощности:
|
|
|
∑ S ист = ∑ S пот . |
|
(58) |
На практике более удобна следующая формула: |
|
|
|||
n |
n |
|
|
||
∑(Ek I *k + |
U |
Jk |
J * ) = ∑(Ik2 Rk + j Ik2 |
( X Lk − X Ck )) , |
(59) |
k =1 |
k =1 |
|
|
||
Если действительные направления ЭДС и тока в некоторой ветви совпадают, то мощность такого источника ЭДС входит в уравнение (59) с положительным знаком и источник отдает энергию в цепь (работает в режиме генератора). Если направления ЭДС и тока ветви противоположны, то мощность источника ЭДС записывается в уравнении (59) с отрицательным знаком и такой источник работает в режиме приёмника, потребляя энергию.
Методы расчета ЛЭЦ при гармоническом воздействии. (МТВ, МКТ, МУН)
Методика расчета ЛЭЦ при гармоническом воздействии такая же, как и на постоянном токе, только в соответствующих уравнениях стоят комплексы напряжений и токов.
R1 |
L |
1 |
|
1 |
|
C3 R3 |
|
Z |
1 |
|
1 |
Z |
3 |
|
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
i1(t) |
i2(t) |
|
|
|
|
|
i(t) |
I1 |
|
I2 |
Z2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
|
R2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||
e(t) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
L2 |
|
E |
|
|
|
|
J |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
C2 |
|
I11 |
|
|
J |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Дано: e (t ) = Em cos (ωt + ϕe ) = E 
 2 cos (ωt + ϕe ) , i (t ) = Jm cos (ωt + ϕi ) = J
2 cos (ωt + ϕe ) , i (t ) = Jm cos (ωt + ϕi ) = J 
 2 cos (ωt + ϕi ) .
2 cos (ωt + ϕi ) .
Для комплексной схемы замещения можно записать: E = E ejϕe , J = J ejϕi .
Z1 = R1 + jω L , Z 2 = R2 + jω L2 + |
|
|
1 |
, Z 3 |
= R3 + |
|
|
1 |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
jωC2 |
|
|
|
|
jωC3 |
|
|
|
|
|||||
По МТВ составляется 2 уравнения: (1) I 2 = I1 + J , (2) |
|
E = I1 Z1 + I 2 Z 2 . |
|
|
|
|
|
|
|
|
||||||||||||
По МКТ составляется 1 уравнение: I11 (Z1 + Z 2 ) + J Z 2 = E , где I1 = I11 , |
I 2 |
= I11 + J . |
||||||||||||||||||||
|
|
|
1 |
|
1 |
1 |
|
|
|
E −V |
|
|
|
|
V |
|
|
|||||
По МУН составляется 1 уравнение: V 1 |
|
+ |
|
= E |
|
|
+ J , I 1 |
= |
|
|
|
1 |
, |
I 2 = |
|
|
1 |
. |
||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Z1 |
|
Z 2 |
Z1 |
|
|
|
Z1 |
|
|
|
|
Z 2 |
||||||||
В результате расчетов получаем комплексные токи ветвей в виде:
I |
1 |
= I ejϕi1 |
, I |
2 |
= I |
2 |
ejϕi2 . |
|
1 |
|
|
|
Далее необходимо представить мгновенные значения токов ветвей:
i1 (t ) = I1 
 2 cos (ωt + ϕi1 ) , i2 (t ) = I2
2 cos (ωt + ϕi1 ) , i2 (t ) = I2 
 2 cos (ωt + ϕi2 ) .
2 cos (ωt + ϕi2 ) .
35 /102
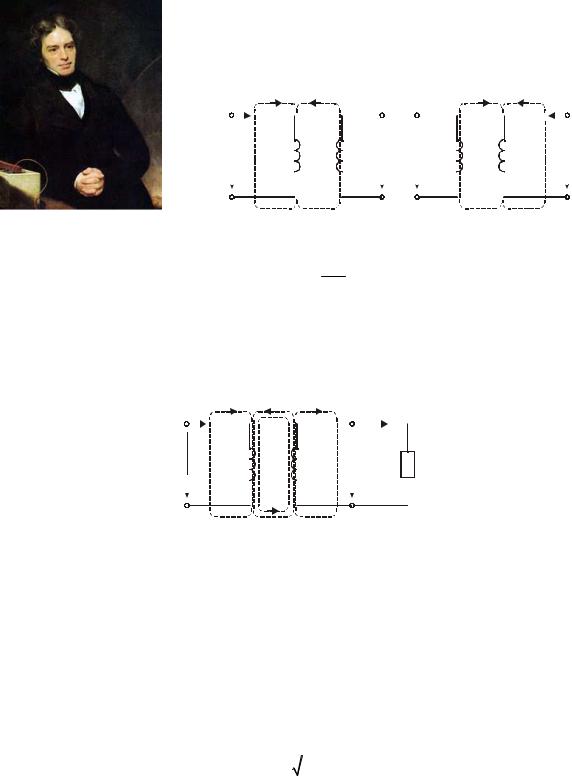
Электрические цепи с индуктивными связями. Основные понятия.
Мы рассматривали цепи без учета явления взаимоиндукции. При протекании переменного тока i1 через катушку индуктивности L1 в окружающем пространстве, согласно закону об электромагнитной индукции (закон Фарадея), создаётся магнитный поток Φ11 . Если какая либо часть этого потока Φ12 пронизывает витки другой катушки L2 , то в ней наводится напряжение взаимоиндукции.
uM2 |
= M12 |
d i1 |
. |
(60) |
|
||||
|
|
d t |
|
|
Майкл Фа?радей(Michael Faraday), 1791-1867,
английский физик, химик и физико-химик
i |
Φ11 |
Φ12 |
|
|
|
Φ21 |
Φ22 |
|
i2 |
|||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
u |
L1 |
|
L2 |
uM2 |
L1 |
|
L2 |
|
|
u |
||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
|
|
|||||||||
|
|
|
|
|
||||||||
|
||||||||||||
|
uM1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если напряжение u приложено к катушке индуктивности L2 , то напряжение взаимоиндукции uM1 возникает на зажимах катушки L1 .
uM1 = M 21 d i2 . (61)
d t
Согласно принципу взаимности M12 = M 21 = M – взаимоиндуктивность [Гн].
Рассмотренная индуктивная связь носит односторонний характер, поскольку ток i1 вызывает напряжение взаимоиндукции uM2 , а ток i2 – напряжение взаимоиндукции uM1 .
В случае замыкания одной из катушек на конечное сопротивление R проявляется
двухсторонняя индуктивная связь. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
i1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2 |
|
|
|
|
u1 |
L1 |
|
|
|
|
|
L2 |
|
|
u2 |
R |
|||||||||
|
|
|
|
|
|
|
Φ21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Φ11 |
|
|
Φ12 |
|
|
|
|
|
|
Φ22 |
|
|
|
|
|
|
|||
В катушке L1 |
индуцируется напряжение u1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
u = L |
di1 |
|
+ M |
di2 |
. |
(62) |
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
1 |
1 d t |
d t |
|
||||||||||||||
В катушке L2 |
индуцируется напряжение u2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
u |
|
|
= L |
di2 |
+ M |
di1 |
. |
(63) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
d t |
|
d t |
|
|||||||||
Включение катушек согласное, |
если |
потоки |
|
само- и |
взаимоиндукции складываются. |
|||||||||||||||||
В противном случае включение встречное. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Степень связи между L1 и L2 оценивается коэффициентом связи: |
||||||||||||||||||||||
|
|
|
|
|
|
|
k = |
|
|
|
|
M |
. |
|
|
|
(64) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
L1 L2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
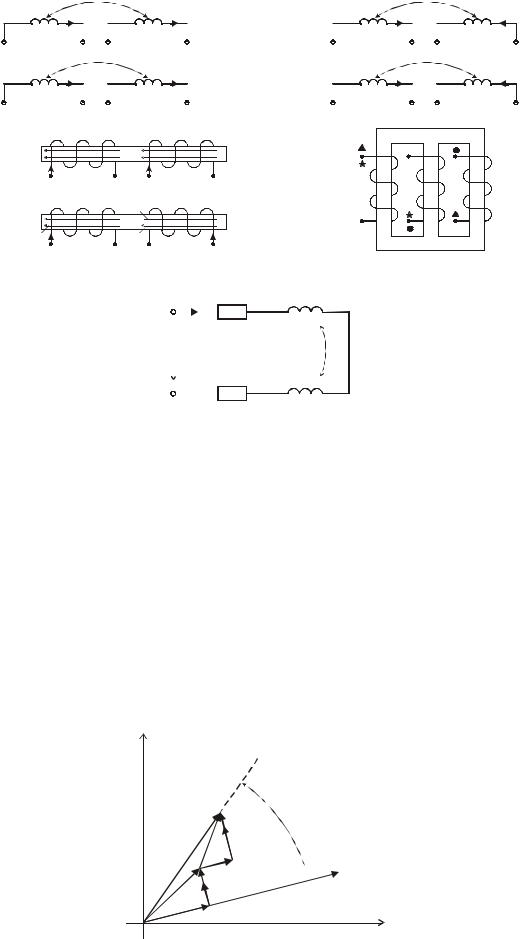
Если k = 1 – жесткая индуктивная связь, если k = 0 – отсутствие индуктивной связи.
36 /102
Для компактности и удобства изображения схем электрических цепей с взаимной индуктивностью вводят понятие одноименных зажимов – узлов, относительно которых одинаково ориентированные токи создают складывающиеся потоки само- и взаимоиндукции.
|
|
M |
|
|
|
|
M |
|
|||
* |
i1 |
|
* |
i2 |
* |
i1 |
|
|
|
* i2 |
|
|
L1 |
|
L2 |
|
согласное включение |
|
L1 |
|
|
|
L2 |
|
|
M |
|
|
|
|
M |
|
|||
* |
i1 |
|
|
* i2 |
|
* |
i1 |
|
|
* |
i2 |
L1 |
|
L2 |
встречное включение |
L1 |
|
L2 |
|||||
|
|
|
|
|
|
|
|||||
Направление магнитных потоков самоиндукции и согласное включение катушек индуктивности
Ф11 |
1 |
Ф21 |
2 |
|
|
|
1 |
2 |
3 |
||
|
|
|
|||
Ф12 |
* |
Ф22 |
* |
|
|
|
|
|
|
||
Ф11 |
1 |
Ф21 |
2 |
|
|
|
|
|
|
||
Ф12 |
* |
Ф22 |
* |
|
|
|
|
|
|
Последовательное соединение катушек индуктивности. Виды включения.
Рассмотрим согласное включение катушек индуктивности:
|
|
|
|
|
|
i(t) R1 |
L1 |
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
u(t) |
M |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
R2 |
L2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
* |
u (t ) = uR1 (t ) + uL1 (t ) + uM (t ) + uR 2 (t ) + uL2 (t ) + uM (t ) . |
|
|||||||
u (t ) = (R + R |
)×i (t ) + ( L + L + 2 M )× |
d i |
. |
|
||||
|
|
|||||||
1 |
2 |
1 |
2 |
|
|
|
|
|
d t
В комплексной форме можно записать:
U = (R1 + R2 ) I + jw(L1 + L2 + 2 M ) I , откуда полное сопротивление цепи:
Z = R1 + R2 + jw( L1 + L2 + 2 M ) .
Фазовый сдвиг между входным током и напряжением определяется:
w(L1 |
+ L2 + 2 M ) |
||
j = arctg |
|
|
. |
|
R1 + R2 |
||
|
|
||
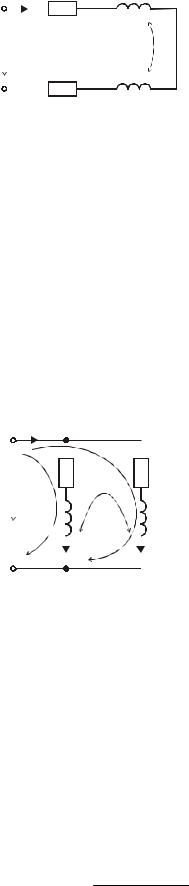
Определим напряжение на катушке L1 с потерями
U 1 = (R1 + jw(L1 + M )) I .
Определим напряжение на катушке L2 с потерями R2 :
U 2 = (R2 + jw(L2 + M )) I .
Построим векторную диаграмму напряжений при согласном включении катушек:
Im |
|
|
|
|
U |
UM |
ϕ |
|
U2 |
UL2 |
|
|
UM |
UR |
|
|
2 |
I |
|
|
|
||
U1 |
UL1 |
|
|
UR1 |
|
||
|
|
||
|
|
|
Re |
37 /102
Рассмотрим встречное включение катушек индуктивности:
|
|
|
|
|
|
i(t) R1 |
L1 |
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
u(t) |
M |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
R2 |
L2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
* |
u (t ) = uR1 (t ) + uL1 (t ) − uM (t ) + uR2 (t ) + uL2 (t ) − uM (t ) . |
|
|||||||
u (t ) = ( R + R |
)i (t ) + ( L + L − 2 M ) |
d i |
. |
|
||||
|
|
|||||||
1 |
2 |
1 |
2 |
d t |
|
|||
|
|
|
|
|
||||
В комплексной форме можно записать:
U= ( R1+R2 ) I+ jω(L1+ L2 −2 M ) I , откуда полное сопротивление цепи: Z=R1+R2 +jω( L1+L2 −2 M ) . Фазовый сдвиг между входным током и напряжением определяется:
ω(L1 |
+ L2 |
− 2 M ) |
||
ϕ = arctg |
|
|
|
. |
|
R1 + |
R2 |
||
|
|
|||
Определим напряжение на катушке L1 с потерями R1 :
U 1 = (R1 + jω(L1 − M )) I .
Определим напряжение на катушке L2 с потерями R2 :
U 2 = (R2 + jω(L2 − M )) I .
Параллельное соединение катушек индуктивности. Виды включения.
Рассмотрим случай согласного включения:
|
|
|
|
|
|
|
|
|
i(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 |
M |
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
u(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
I |
|
|
|
i1(t) |
|
|
L1 |
II |
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i2(t) |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Запишем комплексы токов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I = I1 + I 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(65) |
||||||||||||||||
|
|
|
U = I1 Z1 |
|
+ I 2 Z св = U R |
+ U L |
+ U M |
1 |
, |
(66) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
U = I 2 Z 2 |
|
+ I 1 Z св |
= |
U |
R |
+ U L |
+ U M |
2 |
. |
(67) |
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||||
Z1 = R1 + jω L1 , |
|
|
|
|
|
Z 2 = R2 + jω L2 |
|
|
Z св = jω M . |
||||||||||||||||||||||||||||||||||
Из уравнений (65), (66) и (67) определяем комплексы токов: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
I |
|
= |
|
|
|
U |
|
|
|
|
|
= |
U |
, I |
|
= |
|
|
|
|
U |
|
|
= |
|
U |
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1 |
Z1 Z 2 − Z св2 |
|
|
|
|
2 |
|
Z1 Z 2 − Z св2 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Z1эс |
|
|
|
|
|
|
|
|
|
|
Z 2 эс |
||||||||||||||||||||||||||
|
|
|
|
Z 2 − Z св |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 − Z св |
|
|
|
|
|
|
|
|
|
||||||||||||
С другой стороны эквивалентные сопротивления Z1эс и Z 2эс можно представить: |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Z1эс = Z1 + Z1вн.с. , Z 2эс = Z 2 + Z 2вн.с. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Ток в неразветвленной части цепи определяем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
I = |
|
|
1 |
+ |
|
1 |
= |
|
|
|
|
|
|
|
U |
|
|
|
= |
U |
|||||||||||||||||||||
|
|
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Z1эс |
|
|
|
|
2эс |
|
|
|
|
|
Z1 Z 2 − Z св |
|
|
|
Z эс |
||||||||||||||||||||||
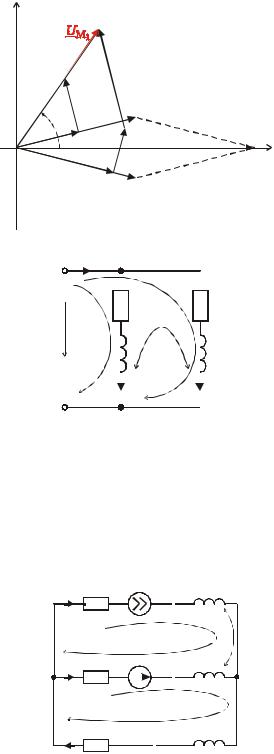
Z1 + Z 2 − 2 Z св
где Z эс эквивалентное сопротивление цепи при согласном включении.
38 /102
Im |
|
|
|
|
|
|
|
|
U |
UM2 |
|
|
|
|
|
|
|
|
|
|
ϕэс |
UL1 |
|
I1 |
|
|
|
|
|
|
|
|
||
|
U |
R1 |
|
UL |
2 |
I |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
UR2 |
I2 |
|
|
||
|
|
|
|
|
|
|
Рассмотрим случай встречного включения: i(t)
|
|
|
|
|
R1 |
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|||
u(t) |
|
|
|
|
M |
|||||
|
* |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
L2 |
||
|
|
|
|
|
|
|
|
|
|
|
I |
i1(t) |
|
L1 |
II |
|
|
* |
|||
|
|
|||||||||
|
|
|
|
|
i2(t) |
|||||
|
|
|
|
|
|
|
|
|
||
Запишем комплексы токов:
|
I = I |
1 |
+ I 2 |
, |
(68) |
|
|
U = I1 |
Z |
1 |
+ I 2 |
Z св , |
(69) |
|
U = I 2 |
Z 2 + I1 Z св . |
(70) |
|||
Z1 = R1 + jω L1 , |
Z 2 = R2 + jω L2 , |
Z св = − jω M . |
||||
Самостоятельно определить эквивалентное сопротивление цепи при встречном включении.
Методы анализа индуктивно-связанных электрических цепей.
При расчете цепей с индуктивными связями отдают предпочтение МТВ и МКТ. Схема № 1:
J |
R1 |
|
J |
C1 L |
1 * |
||||
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
M |
||
|
|
|
|
|
|
|
|||
I2 R2 |
|
E |
|
C2 L2 * |
|||||
|
|||||||||
|
|
|
|
|
|
|
|
||
Расчёт по МТВ.
(2) E = I 2 R2
Расчёт по МКТ.
I11
I3
+ jω L2 +
R3 |
|
|
|
|
C |
L |
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
(1) |
I 3 = I 2 + J , |
|
||||
1 |
|
|
+ jω M J |
+ I 3 |
||
|
|
|
||||
|
|
|||||
jωC2 |
|
|
|
|
||
|
+ jω L3 + |
1 |
|
|
R3 |
|
. |
||
jωC |
||||
|
|
|
||
|
3 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
I 11 R2 |
+ R3 + j |
ω L2 |
+ ω L3 |
− |
|
|
− |
|
|
|
− J R2 |
+ j |
ω L2 |
ωC |
|
ωC |
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
|
||||||
Выразим комплексные токи ветвей: I 3 = I11 , I 2 |
= I11 − J . |
|
|
||||||||||
− |
1 |
|
+ J jω M = E . |
|
|
||
|
|||
|
ωC2 |
|
|
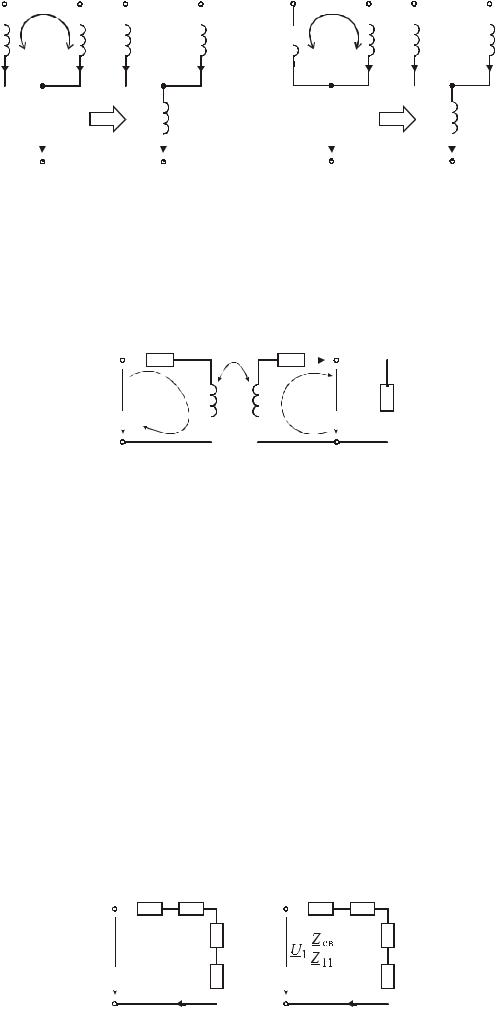
Метод развязки индуктивной связи.
Заключается в составлении эквивалентных схем, не содержащих индуктивные связи.
|
|
M |
|
|
|
|
L1−M |
|
|
L2−M |
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
L1 |
|
L2 |
|
|||||||||
|
|
* |
|
|
* |
|
|
i1(t) |
|
|
i2(t) |
|
|
|
|
|
|
|
|
||||||
|
|
i1(t) |
|
i2(t) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
M |
||
|
|
|
i(t) |
|
|
|
|
|
|
i(t) |
||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 
*
 i1(t)
i1(t)
39 /102
M |
|
*L2 |
|
|
|
L1+M |
|
|
L2+M |
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
|
|
i2(t) |
|
|
i1(t) |
|
|
i2(t) |
||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
−M |
||
|
|
|
|
|
|
|
|
|
|||
|
i(t) |
|
|
|
i(t) |
||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Самостоятельно провести развязку индуктивной связи по схеме № 1. Составить эквивалентную схему замещения без индуктивной связи.
После развязки индуктивной связи можно применять такие методы как: МУН и метод эквивалентного генератора.
Анализ воздушного электрического трансформатора. Схемы замещения.
Трансформатором называют статическое устройство, предназначенное для преобразования значений переменных напряжений и токов. Трансформатор состоит из двух индуктивно связанных
катушек индуктивности L1 и L2 , |
расположенных на общем сердечнике. Катушка, к которой |
|||||||||||||
подключается источник – первичная, к которой подключается нагрузка – вторичная. |
||||||||||||||
|
|
R1 |
i1(t) |
M |
|
|
R2 |
i |
2 |
(t) |
|
|||
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
|
|
u1(t) |
L1 |
|
|
|
L2 |
|
u2(t) |
Zн |
|||||
|
|
I |
|
|
|
|
|
|
||||||
|
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сопротивление нагрузки в общем случае комплексное: Z н = Rн + j X н . Составим уравнения по 2 закону Кирхгофа для I и II контуров
|
|
|
|
|
|
|
|
|
|
U 1 = Z11 I1 − Z св I 2 , 0 = Z 22 I 2 − Z св I1 . |
|
|
|
|
|
|
|
(71) |
||||||||||||||||||||||||||||||||||
Z11 = R11 + j X11 = R1 + jω L1 , то есть R11 = R1 , |
|
X11 = ω L1 ; Z св = j X св |
= jω M , то есть X св = ω M ; |
|||||||||||||||||||||||||||||||||||||||||||||||||
Z 22 = R22 + j X 22 = R2 + Rн + j(ω L2 + X н ) , то есть R22 = R2 + Rн , |
X 22 |
= ω L2 + X н . |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
Из уравнений (71) определяем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
I 1 |
= I 2 |
Z 22 |
, далее U 1 = Z11 I 2 |
Z 22 |
− Z св I 2 , откуда определяем: |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Z св |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Z св |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U 1 |
Z св |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
I |
|
= |
|
U 1 Z св |
|
|
|
= |
Z11 |
|
|
, тогда I |
|
= |
|
|
|
|
|
U |
1 Z 22 |
|
= |
|
|
U |
1 |
. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
2 |
|
Z11 Z 22 − Z св2 |
Z 22 |
− |
|
Z |
св2 |
|
1 |
|
|
Z11 Z 22 − Z св2 |
Z11 − |
Z св2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 22 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Введем понятие вносимых сопротивлений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
Z |
1вн |
= − |
Z св2 |
= R |
|
|
+ j X |
|
|
, Z |
2вн |
= − |
Z св2 |
|
= R |
|
+ j X |
|
. |
|
|
|
(72) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1вн |
|
|
|
|
2вн |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Z 22 |
|
|
1вн |
|
|
|
|
|
|
|
|
|
|
|
|
Z11 |
|
|
2вн |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Комплексы токов можно записать как: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
Z св |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
1 |
= |
|
|
|
U |
1 |
|
|
|
, I 2 |
= |
|
|
|
1 |
Z11 |
|
|
. |
|
|
|
|
|
|
|
|
|
(73) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Z11 + Z1вн |
|
Z 22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ Z 2вн |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Уравнения (73) соответствуют одноконтурным схемам замещения трансформатора. |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
R11 |
|
|
X11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R22 |
X22 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
вн |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
вн |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
U1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
X1вн |
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
X2вн |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||

40 /102
Из уравнений (72) получим в явном виде вносимые сопротивления:
|
|
|
|
|
|
|
|
X св2 |
|
|
|
|
|
|
X св2 |
|
|
|
|
|
|
|
|
|
X св2 |
|
|
|
|
|
|
|
|
X св2 |
|
|
||||||||||||||||
R1вн = |
|
|
|
|
|
|
|
|
|
|
|
R22 , R2вн = |
|
|
|
|
|
|
|
|
|
R11 , X1вн = − |
|
|
|
X 22 , X 2вн = − |
|
|
|
X11 . |
||||||||||||||||||||||
R2 |
|
+ X 2 |
|
R2 |
+ X 2 |
R2 |
+ X 2 |
R2 + X |
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
22 |
|
|
|
22 |
|
|
|
|
|
11 |
|
|
|
11 |
|
|
|
|
|
22 |
|
22 |
|
|
|
|
|
|
|
|
|
|
11 |
|
11 |
|
||||||||||||
С физической точки |
зрения R1вн |
и R2вн представляют собой |
эквивалентные |
|
резистивные |
|||||||||||||||||||||||||||||||||||||||||||||||
сопротивления, вносимые за счёт взаимной индуктивности соответственно в контуры I и II. При |
||||||||||||||||||||||||||||||||||||||||||||||||||||
этом на R1вн при протекании тока I1 |
|
рассеивается та же мощность, что и на R2 при протекании |
||||||||||||||||||||||||||||||||||||||||||||||||||
тока I 2 и соответственно на R2вн |
при протекании тока I 2 |
рассеивается та же мощность, что и на |
||||||||||||||||||||||||||||||||||||||||||||||||||
R1 при протекании тока I1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Определим отношение комплексных токов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 1 |
= |
Z 22 |
= |
R2 + Rн + j(ω L2 + X н ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
I 2 |
|
Z св |
|
|
|
jω M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В отсутствии потерь R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
I |
1 |
|
|
|
|
Rн + j(ω L2 + X |
н ) |
|
|
|
jω L R + j X |
н |
|
L |
Z |
н |
|
1 |
|
Z |
н |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
2 |
+ |
н |
= |
2 |
+ |
|
|
= |
|
+ |
|
|
, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jω M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
I 2 |
|
|
|
|
|
|
|
|
|
jω M jω M M Z св |
|
kтр |
|
Z св |
|
|
|
||||||||||||||||||||||||||
где kтр = |
M |
= |
|
|
|
|
|
1 |
|
|
|
|
|
– коэффициент трансформации. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
I1 |
|
|
|
Z н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
L |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
I 2 |
|
|
|
Z св |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Определим отношение напяжений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
I 2 |
Z11 Z 22 − Z св2 |
(R1 + jω L1 ) (R2 + Rн + j(ω L2 + X н )) − ( jω M ) |
2 |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
U |
1 |
= |
Z |
св |
|
|
= |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( Rн + j X н ) jω M |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
U 2 |
|
|
|
|
|
|
|
I 2 Z н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Отношение, как комплексных токов, так и напряжений в воздушных трансформаторах с потерями
зависит отсопротивления нагрузки Z н . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
В отсутствии потерь R1 = R2 |
= 0 имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
U |
1 |
= |
jω L1 (Rн + j(ω L2 + X н )) + (ω M )2 |
|
= |
|
|
jω L1 (Rн + j X н ) + jω L1 jω L2 |
+ (ω M )2 |
, далее |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
U 2 |
|
|
|
( Rн + j X н ) jω M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Rн + j X н ) jω M |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
U |
|
|
jω L |
jω L1 jω L2 + (ω M )2 |
|
|
jω L |
|
−ω2 L1 L2 + (ω M )2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
U |
1 |
= jω M + |
|
( R + j X |
|
) jω M |
|
= jω M |
+ (R + j X |
|
) jω M . |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Считаем, что индуктивная связь жесткая, то есть коэффициент связи |
|
k = |
1 , тогда |
k = |
|
M |
|
= 1 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
L1 L2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда M 2 |
= L L . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, отношение напряжений запишем в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
1 |
|
= |
L |
|
= |
|
M 2 |
1 |
|
|
= |
|
M |
= kтр . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U 2 |
M |
|
|
L2 |
M |
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
kтр |
= |
M |
= |
L1 |
= |
|
|
= |
|
|
|
L1 |
|
|
|
|
= |
|
|
|
L1 |
|
, либо kтр = |
M |
= |
L1 |
|
= |
|
U |
1 |
. |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 L2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L2 |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
L2 |
|
|
M U 2 |
|
|
|
|
|
|||||||||||||||||||||||
Окончательно имеем формулу для определения коэффициента трансформации:
kтр = |
U 1 |
= |
|
L1 |
. |
|
|
|
(74) |
||||
|
|
|
|
|
|
||||||||
|
|
U |
2 |
|
|
|
L2 |
|
|
|
|
||
|
|
|
|
|
|||||||||
Для идеального трансформатора выполняются условия: R1 = R2 = 0 |
и L1 = L2 → ∞ . Коэффициент |
||||||||||||
трансформации идеального трансформатора определяется как: |
|
||||||||||||
kтр∞ = |
U 1 |
|
= |
w1 |
= |
I 2 |
. |
(75) |
|||||
|
|
w2 |
|
||||||||||
|
|
|
|
U 2 |
|
|
|
|
I1 |
|
|||
w1 и w2 – число витков первичной и вторичной катушек.
