§ 8. Геометрические приложения

Уравнение касательной плоскости к поверхности в точке :

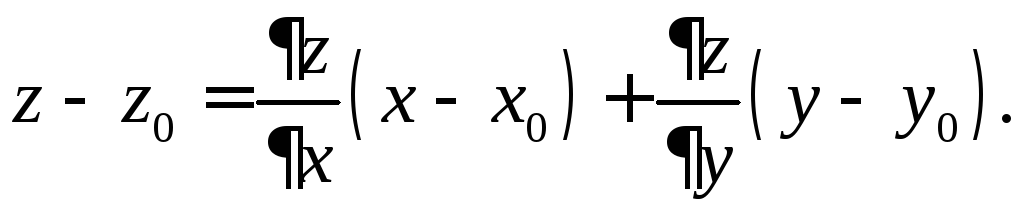
Уравнение нормали к поверхности в точке :

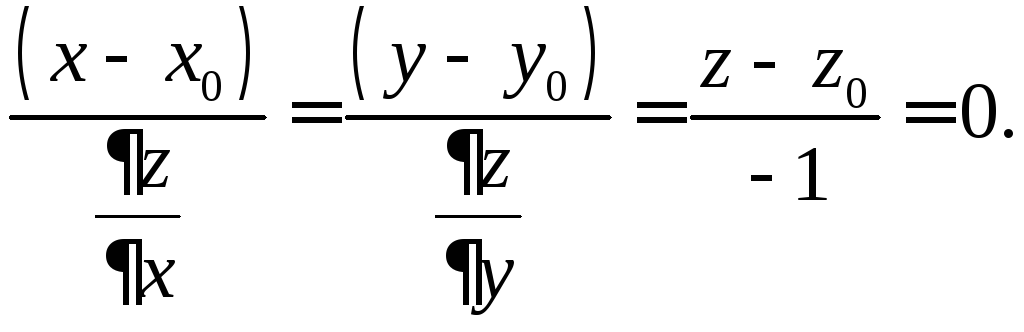
Нормаль – это прямая, перпендикулярная касательной плоскости в точке .

Если функция задана неявно , то уравнение касательной плоскости к поверхности в точке запишется следующим образом:

.

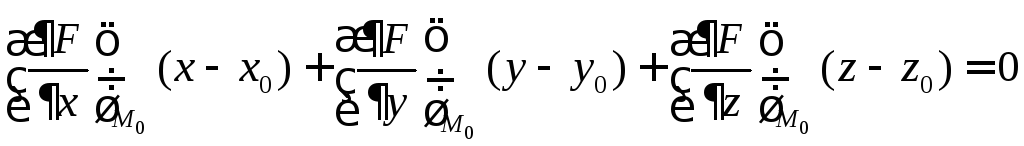Уравнение нормали

.

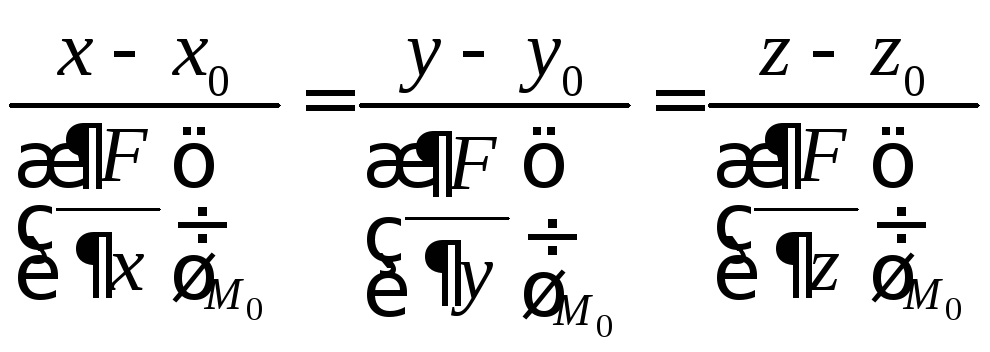Это уравнение прямой в каноническом виде, известном из курса аналитической геометрии.

Пример 8.1. Найти уравнения касательной плоскости и нормали к поверхности : в точке .

Решение. Запишем уравнение поверхности в неявном виде:

.

Уравнение касательной плоскости к поверхности в точке :

.

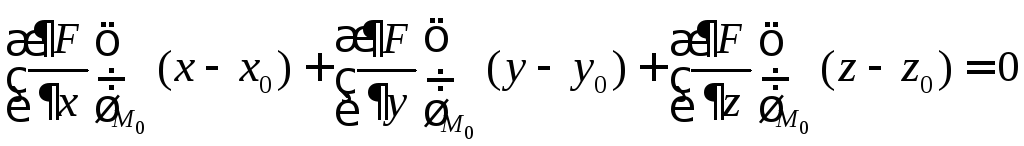Найдем частные производные в точке :

.

Тогда уравнение касательной плоскости к поверхности в точке

, или .

Уравнение нормали к поверхности :

,

.

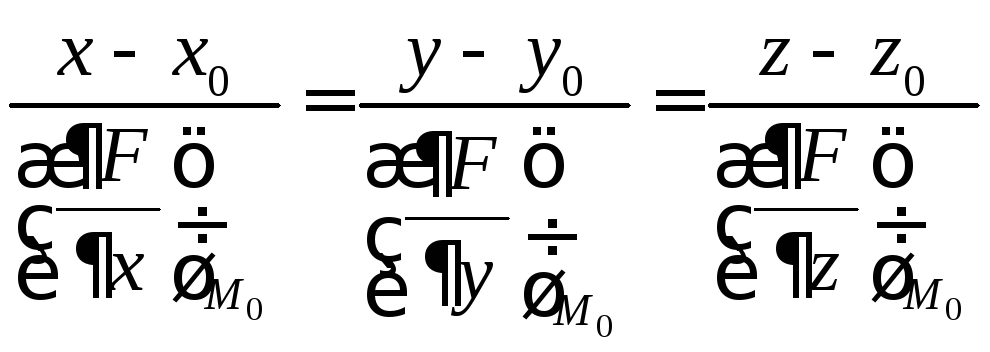Написать уравнения касательных прямых и нормальных плоскостей в данных точках к следующим кривым:

8.1. , , , в точке .
8.2. , , в точке .
8.3. ,, в точке.

8.4. Доказать, что касательная к винтовой линии , , образует постоянный угол с осью .

8.5. Доказать, что кривая , , пересекает все образующие конуса под одним и тем же углом.

8.6. Найти производную функции 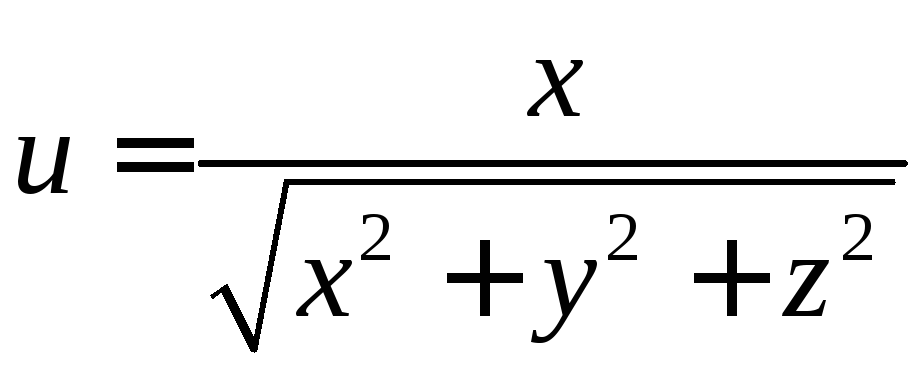в точкев направлении касательной в этой точке к кривой ,.

Написать уравнения касательной плоскости и нормали в точке к следующим поверхностям:

8.7. ,.	8.8. ,.
8.9. ,.
8.10. , ,,.

8.11. На поверхности найти точки, в которых касательные плоскости параллельны координатным плоскостям.

8.12. Найти огибающую кривую однопараметрического семейства плоских кривых: .

8.13. Найти огибающую кривую эллипсов 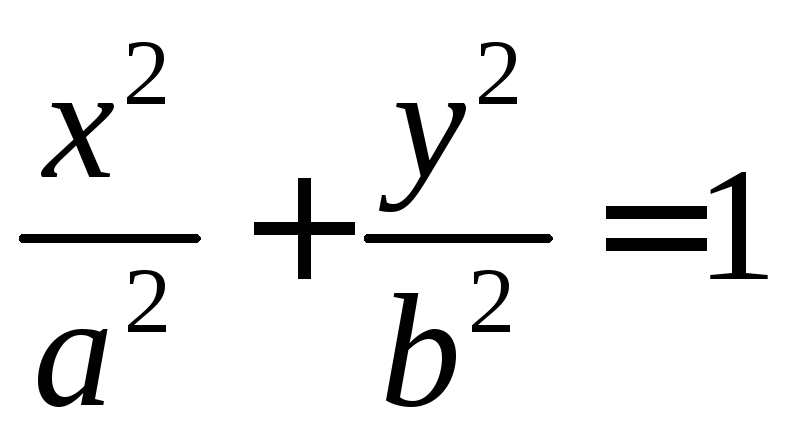, имеющих постоянную площадьS.

8.14. Найти огибающую кривую семейства шаров

,

где и t – переменный параметр.

Ответы: 8.1. . 8.2. ; . 8.3. . 8.6. .

8.7. . 8.8.

. 8.9. .

8.10. 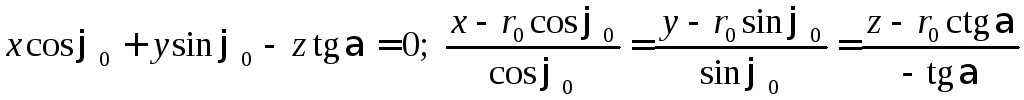. 8.11. . 8.12. .

8.13. . 8.14.

.

§ 9. Формула Тейлора и ряд Тейлора

Пусть функция в окрестности точкиимеет непрерывные производные до порядкавключительно. Тогда в этой окрестности справедливаформула Тейлора

,

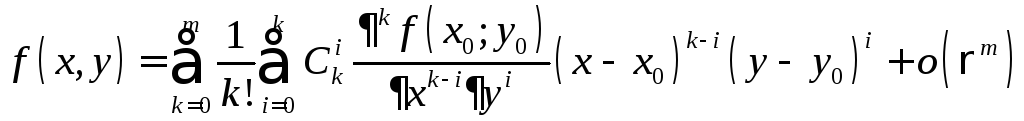где

,

а – остаточный член в форме Пеано.

В частном случае при эту формулу называютформулой Маклорена.

Если функция в окрестности точкиимеет непрерывные производные всех порядков, то ряд

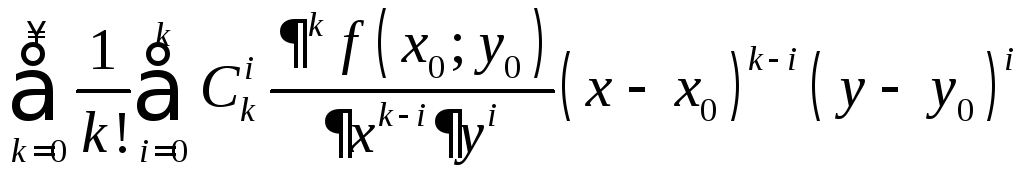
называют рядом Тейлора функции в точке. Если этот ряд сходится в некоторой окрестности точкик функции, то говорят, что в этой окрестности функцияразлагается в ряд Тейлора. В частном случае приэтот ряд называютрядом Маклорена.

Пример 9.1. Разложить функцию по формуле Тейлора в окрестности точки .

Решение. Используем формулу Тейлора для функции двух переменных:

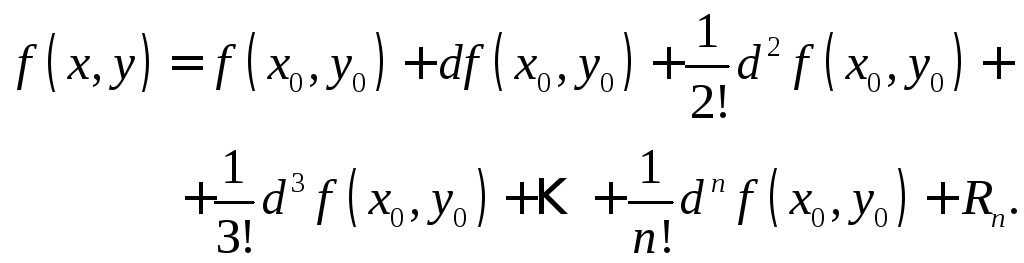
Найдем функцию и частные производные последовательно первого, второго, третьего, порядков в точке :

;

;

;

.

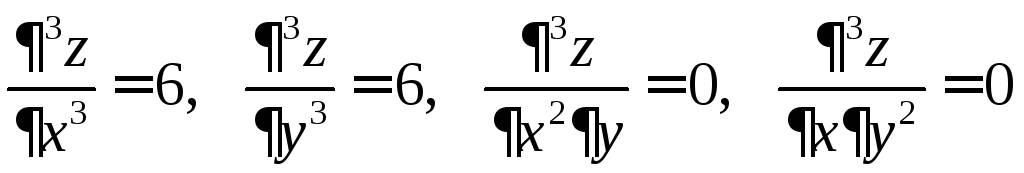Далее все частные производные равны нулю. Подставим найденные производные в формулу Тейлора, принимая :

.

Таким образом, функция разложена по формуле Тейлора без остатка:

.

9.1. Функцию разложить по формуле Тейлора в окрестности точки.

9.2. Найти приращение, получаемое функцией при переходе от значенийк значениям,.

9.3. В разложении функции в окрестности точкивыписать члены до второго порядка включительно.

9.4. Упростить выражение

,

считая малыми по модулю.

Разложить в ряд Маклорена следующие функции:

9.5. .

9.6. .

9.7. Написать разложение в ряд Тейлора функции 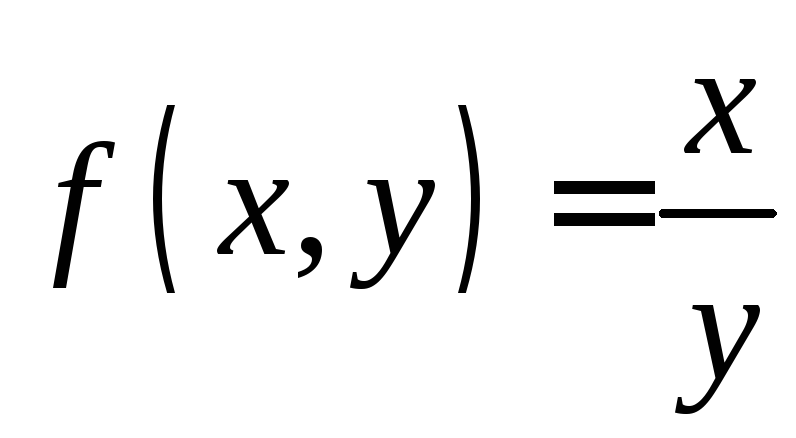в окрестности точки.

9.8. Пусть – та неявная функция оти, определяемая уравнением, которая припринимает значение. Написать несколько членов разложения функциипо возрастающим степеням биномов.

Ответы:

9.1. .

9.2. .

9.3. ,

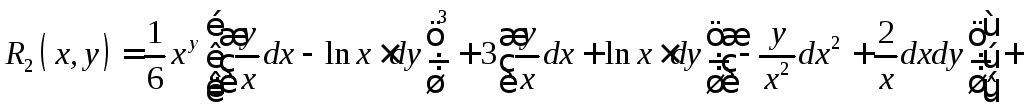
где 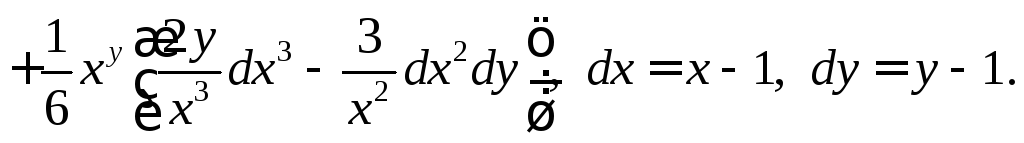9.4. .

9.5. .

9.6. , .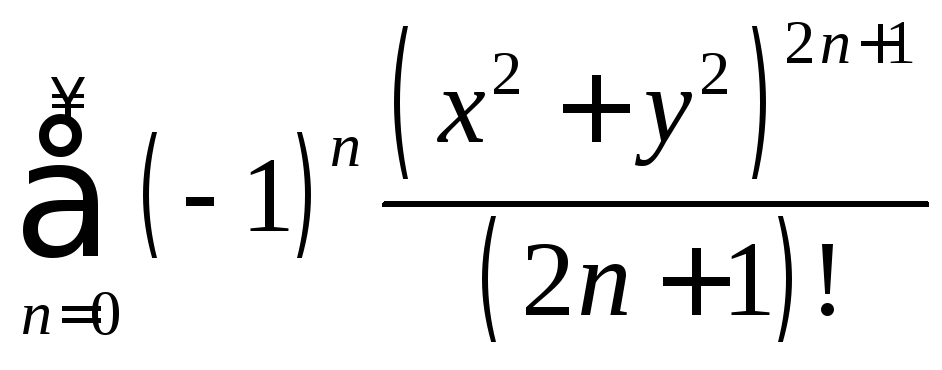

9.7. .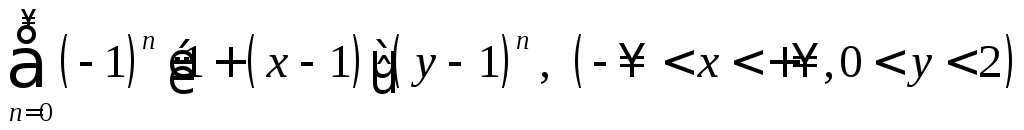

9.8.