§ 7. Замена переменных

Рассмотрим несколько способов дифференциальных замен.

1. Замена переменных в выражении, содержащем обыкновенные производные. Пусть в дифференциальном выражении

требуется перейти к новым переменным: независимой переменной и функции, связанным с прежними переменнымииуравнениями

.

Дифференцируя эти уравнения, имеем:

Аналогично выражаются производные высших порядков В результате получаем

.

2. Замена независимых переменных в выражении, содержащем частные производные. Если в дифференциальном выражении

положить , гдеи– новые независимые переменные, то последовательные частные производныеопределяются из следующих уравнений:

Последовательно дифференцируя эти уравнения, получают производные высших порядков.

3. Замена независимых переменных и функции в выражении, содержащем частные производные. В общем случае, если имеем уравнения

,

где и– новые независимые переменные,– новая функция, то для частных производныхполучаем такие уравнения:

Производные высших порядков получают последовательным дифференцированием этих уравнений.

Пример 7.1. Найти якобиан отображения

.

Решение. Так как

,

то

.

Пример 7.2. Преобразовать выражение к новым переменным, если.

Решение. Найдем частные производные и, используя частные производные функциипо переменными. Продифференцируем обе части равенствапо переменными:

;

Следовательно,

.

Выразим ичерез новые переменные. Так как . Тогда исходное уравнение примет вид

.

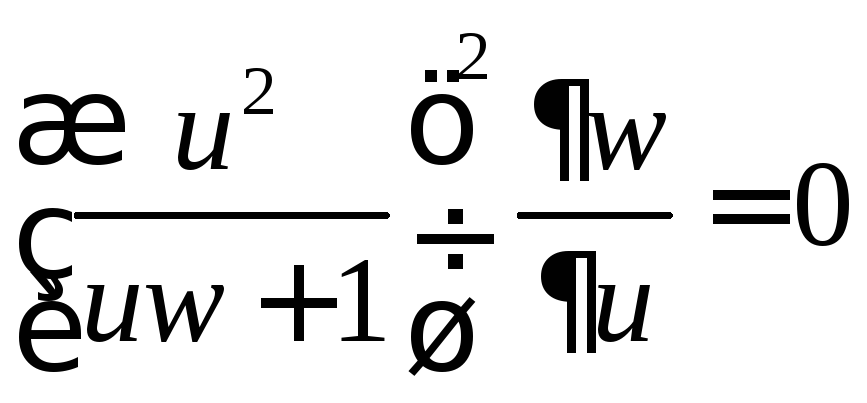7.1. Преобразовать уравнение , принявза функцию и– за независимое переменное.

Введя новые переменные, преобразовать следующие обыкновенные дифференциальные уравнения:

7.2. , если.

7.3. , если.

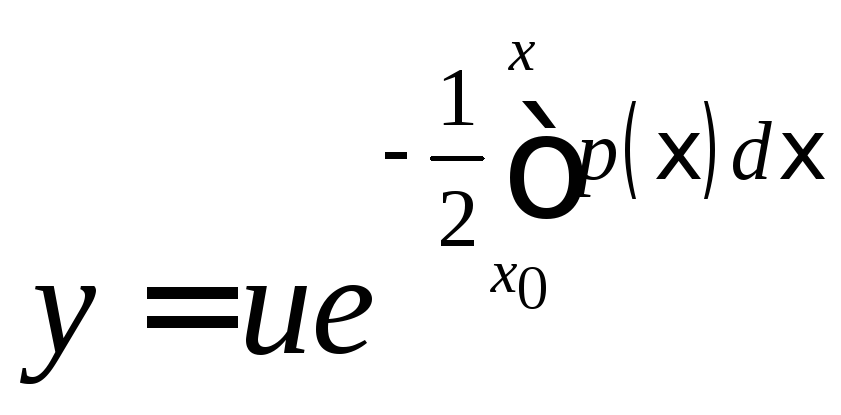7.4. , если, где.

7.5. , еслии, где.

7.6. Преобразовать к полярным координатам и, полагая,, следующее уравнение:.

7.7. Преобразовать к полярным координатам выражение .

7.8. Преобразовать выражение , введя новые функции,.

7.9. Введя новые независимые переменные и, решить следующее уравнение: , если и.

7.10. Приняв u и v за новые независимые переменные, преобразовать следующее уравнение: , если и.

7.11. Преобразовать выражени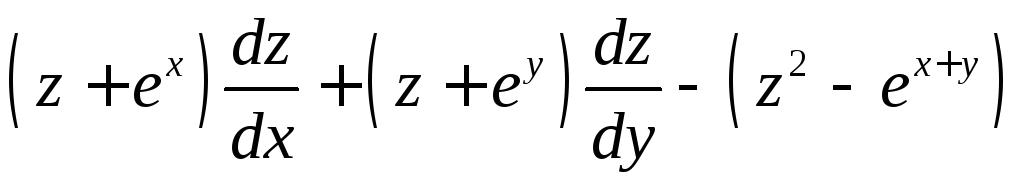е , приняв за новые независимые переменные,.

7.12. Преобразовать выражение ,приняв x за функцию, а ,– за независимые переменные.

Перейти к новым переменным u, v, w, где , в следующих уравнениях:

7.13. , если ,,.

7.14. , если ,,.

Преобразовать к полярным координатам r и , полагая,, следующие выражения:

7.15. .

7.16. .

7.17. .

Приняв u и v за новые независимые переменные, преобразовать следующие уравнения:

7.18. 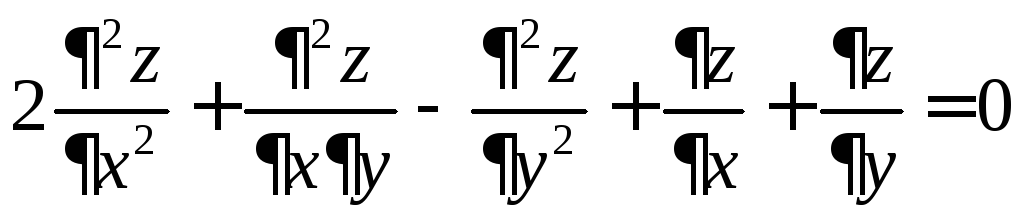, если и.

7.19. 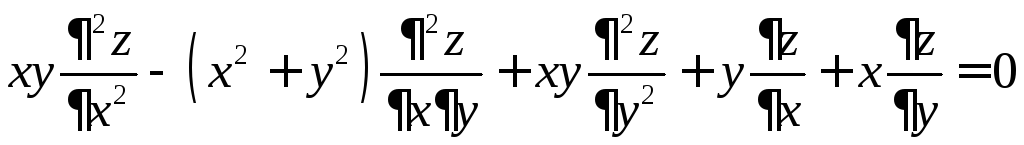, если и.

7.20. Показать, что уравнение не меняет своего вида при замене переменных и.

Приняв u и v за новые независимые переменные и за новую функцию, преобразовать следующие уравнения:

7.21. 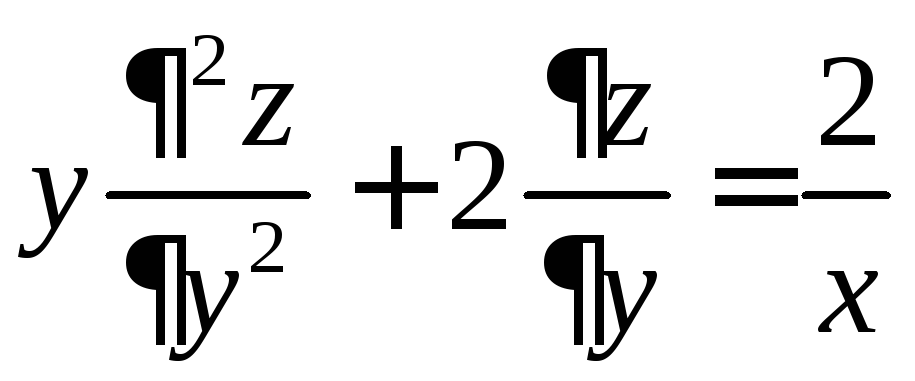, если ,,.

7.22. , если ,,.

7.23. Найти в точке дифференциал отображения.

7.24. Найти в точке (0;0) производную отображения и исследовать его на дифференцируемость в этой точке:

1) ;
2) .

7.25. Найти якобиан отображения:

1) ;

2) .

Ответы: 7.1. . 7.2. . 7.3. . 7.4. . 7.5. . 7.6. . 7.7. . 7.8. . 7.9. . 7.10. . 7.11. . 7.12. . 7.13. . 7.14. . 7.15. .

7.16. . 7.17. . 7.18. .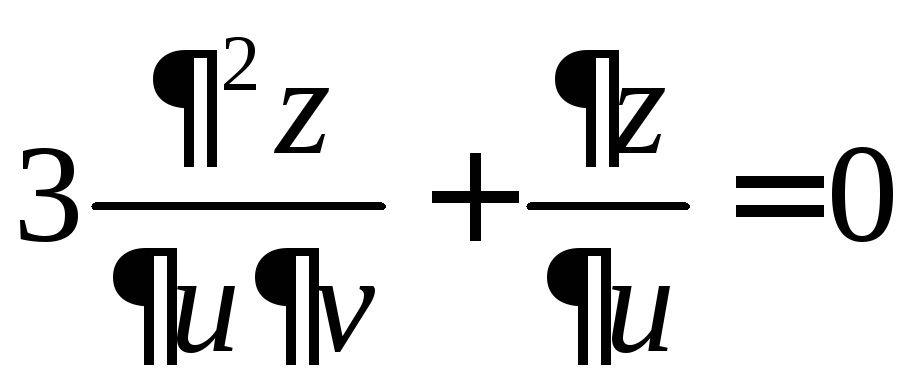

7.19. . 7.21. . 7.22. .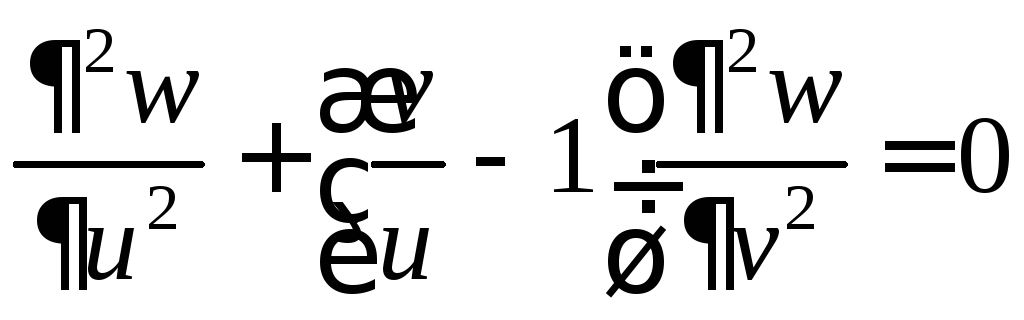

7.23. . 7.24. 1) , дифференцируемо; 2) , недифференцируемо. 7.25. 1) ; 2).