Размещено на http://www.allbest.ru/

Международный университет природы, общества и человека «Дубна»

кафедра высшей и прикладной математики

кафедра системного анализа и управления

Курсовая работа по линейной алгебре

и аналитической геометрии

на тему:

«Исследование кривых и поверхностей второго порядка»

выполнил: студент группы 1202 Пелеванюк И.С.

руководители: доцент Казача Г.С.

доцент Шевцов В.Ф.

Дубна, 2008

Оглавление

Введение 3

Постановка задачи 3

1.Общая теория кривых второго порядка 4

1.1 Кривые второго порядка 4

1.2 Классификация кривых второго порядка 5

2.Исследование кривой второго порядка 7

2.1 Определение зависимости типа кривой от параметра с помощью инвариантов 7

кривая поверхность порядок 9

2.2 Построение кривых при различных значениях параметра 9

2.3 Приведение уравнения кривой при β = 0 к каноническому виду 10

2.4 Определение эксцентриситета, фокусов, директрис, асимптот данной кривой второго порядка 12

2.5 Построение кривой второго порядка в общей и канонической системах координат 13

3.Общая теория поверхностей второго порядка 16

3.1 Поверхности второго порядка 16

3.2 Исследование формы поверхности второго порядка методом сечения плоскостями 17

4. Исследование поверхности второго порядка 19

4.1 Приведение уравнения поверхности к каноническому виду 19

4.2 Исследование формы поверхности методом сечений плоскостями 19

4.3 Построение поверхности в канонической системе координат 28

Вывод 29

Список используемой литературы 30

Введение Постановка задачи

Задание 1. Для данного уравнения кривой второго порядка с параметром :

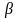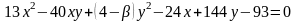
1. Определить зависимость типа кривой от параметра β с помощью инвариантов.

2. Построить кривые всех возможных типов для данного уравнения с параметром.

3. Привести уравнение кривой при β = 0 к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.

4. Найти фокусы, директрисы, эксцентриситет и асимптоты (если они есть) данной кривой второго порядка.

5. Построить кривую в канонической и общей системах координат.

Задание 2. Для данного уравнения поверхности второго порядка:

.

1. Привести уравнение поверхности к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.

2. Исследовать форму поверхности методом сечений и построить полученные сечения.

3. Построить поверхность в канонической системе координат.

1.Общая теория кривых второго порядка

1.1 Кривые второго порядка

Пусть кривая Г задана в декартовой прямоугольной системе координат xOy уравнением:

. (1.1)

Если хотя бы один из коэффициентов отличен от нуля, то кривую Г называют кривой второго порядка.

Теорема 1. Для произвольной кривой второго порядка 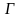существует такая декартова прямоугольная система координат XO'Y, что в этой системе кривая Г имеет уравнение одного из следующих канонических видов:

1) , а  b > 0 — эллипс;

2) 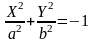— мнимый эллипс;

3) 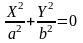— две мнимые пересекающиеся прямые;

4) — гипербола;

5) — две пересекающиеся прямые;

6) — парабола;

7) — две параллельные прямые;

8) — две мнимые параллельные прямые;

9) 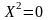— две совпадающие прямые.

В этих уравнениях a, b, p — положительные параметры.

Систему координат XO'Y назовем канонической системой координат, а систему координат xOy — общей системой координат.

Функция 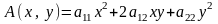называется квадратичной формой, соответствующей уравнению (1.1).

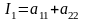,(1.2)

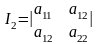.(1.3)

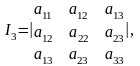(1.4)

Значения не меняются при переходе от одной декартовой прямоугольной системы координат к другой, полученной в результате поворота осей координат и переноса начала координат, то есть являются инвариантами кривой Г относительно поворота осей координат и переноса начала.

1.2 Классификация кривых второго порядка

В зависимости от значения инварианта 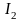принята следующая классификация кривых второго порядка.

Если кривая второго порядка Г называется кривой эллиптического типа.

Если кривая второго порядка Г называется кривой параболического типа.

Если кривая второго порядка Г называется кривой гиперболического типа.

Кривая второго порядка Г называется центральной, если .

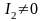Кривые эллиптического и гиперболического типа являются центральными кривыми.

Центром кривой второго порядка Г называется такая точка плоскости, по отношению к которой точки этой кривой расположены симметрично парами. Точка является центром кривой второго порядка, определяемой уравнением (1.1), в том и только в том случае, когда ее координаты удовлетворяют уравнениям:

(1.5)

Определитель этой системы равен . Если , то система имеет единственное решение. В этом случае координаты центра могут быть определены по формулам:

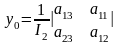, .(1.6)

Классификация кривых второго порядка в зависимости от инвариантов:

1) эллипс — ;

2) мнимый эллипс — ;

3) две мнимые пересекающиеся прямые (точка) — ;

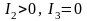4) гипербола — ;

5) две пересекающиеся прямые — ;

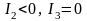6) парабола — ;

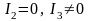7) две параллельные прямые — ;

8) две мнимые параллельные прямые — ;

9) две совпадающие прямые — .