Laboratorny_praktikum_EPiV

УДК 621.372.8 ББК 32.86-01

Э455

Составители: А.С. Волошин, В.С. Панько

Э455 Электромагнитные поля и волны: лабораторный практикум для студентов специальности 210406.65 «Сети связи и системы коммутации» и направления 210400.62 «Телекоммуникации» [Электронный ресурс] /сост. А.С. Волошин, В.С. Панько. – Красноярск: Сиб. федер. ун-т, 2012. – 1 диск. – Систем. требования: Pentium 200 МГц и выше, 256 Мб оперативной памяти, 50 Мб свободного места на жестком диске, Windows 98 и выше. – Загл. с экрана – Электромагнитные поля и волны. Лабораторный практикум.

Приведены 5 лабораторных работ по основным разделам дисциплины. Даны краткие теоретические сведения, порядок выполнения работ.

Предназначен для студентов специальности 210406.65 «Сети связи и системы коммутации» и направления 210400.62 «Телекоммуникации».

УДК 621.372.8 ББК 32.86-01 © Сибирский федеральный

университет, 2012

2

ВВЕДЕНИЕ

Выполнение лабораторных работ является обязательной составляющей при изучении дисциплины «Электромагнитные поля и волны». Настоящий лабораторный практикум составлен в соответствии с Государственным образовательным стандартом.

Цель настоящего издания – научить студентов применять физические законы, изучаемые в теоретическом курсе, к решению конкретных практических задач. Также при выполнении лабораторных работ студенты приобретают основные навыки исследовательской работы, учатся правильно пользоваться современными измерительными приборами и аппаратурой, знакомятся с методами измерений различных физических величин и обработкой полученных результатов, что является хорошей предпосылкой успешной дальнейшей работы

инаучной деятельности.

Впрактикуме приведены 5 лабораторных работ, которые студентам нужно выполнить в пятом семестре при изучении дисциплины «Электромагнитные поля и волны».

Каждая работа содержит теоретический материал, в котором кратко изложены принципы работы рассматриваемого устройства, а также суть и актуальность проводимого исследования. Кроме того, во всех лабораторных работах подробно раскрывается экспериментальная часть метода, положенного в основу изучения каждого опыта, а также приводится порядок выполнения работы и техника обработки результатов. Для детальной проработки пройденного материала и закрепления полученных знаний в конце каждой работы приведены контрольные вопросы. С целью помочь студентам найти ответы на контрольные вопросы в завершении описания к каждой из работ также приведен соответствующий библиографический список рекомендуемой литературы.

Настоящий лабораторный практикум предназначен для студентов радиотехнических специальностей вузов.

3

Лабораторная работа № 1

ИЗМЕРИТЕЛЬНАЯ ЛИНИЯ

Цель работы: Изучить устройство измерительной линии, освоить ее настройку и методы измерения на ней. Освоить методику определения нормированных сопротивлений СВЧ-нагрузок с помощью измерительной линии.

Конструкция и принцип действия измерительных линий

Измерительными линиями называются приборы, позволяющие измерять распределение поля вдоль линии передачи. С помощью измерительной линии определяют коэффициент стоячей и бегущей волны, коэффициент отражения, полное сопротивление нагрузки.

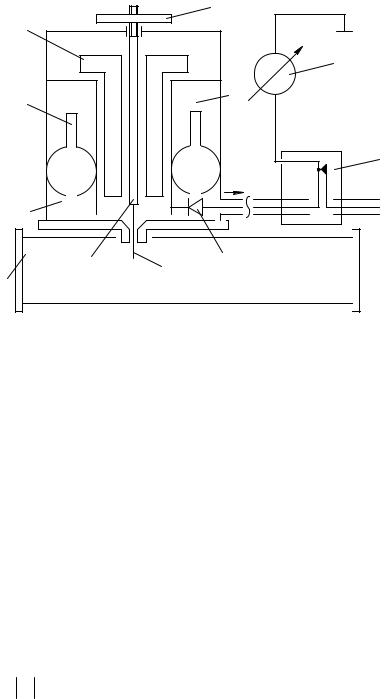
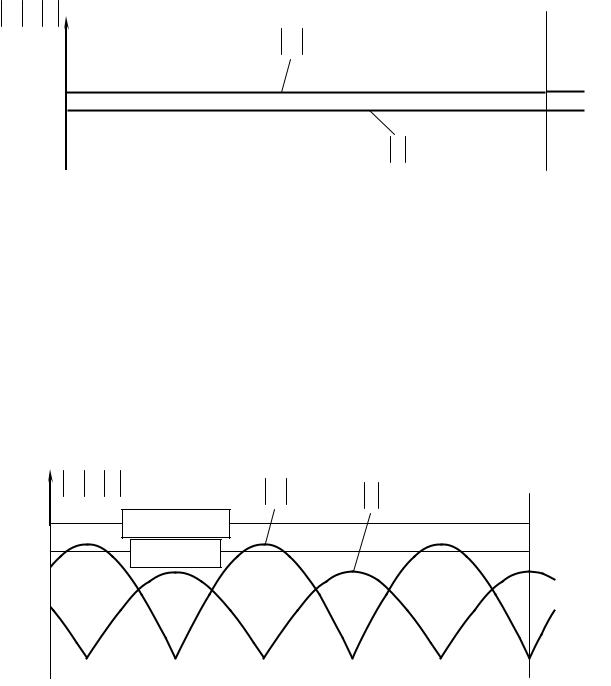
Наибольшее распространение получили коаксиальные и волноводные измерительные линии. Основой волноводной измерительной линии является отрезок волновода прямоугольного сечения с продольной щелью, прорезанной в середине его широкой стенки (рис. 1.1). Вдоль щели передвигается каретка с зондом, который соединяется с резонатором. Длина измерительной линии выбирается таким образом, чтобы вдоль нее укладывалось не менее 5-6 длин волн.

Настройка измерительной линии сводится к получению точного резонанса в камере детекторной секции (по максимальному показателю индикатора) и подбору оптимальной глубины погружения зонда в волновод. Резонансная система линии состоит из двух резонаторов, настройка которых производится путем перемещения поршней с использованием внешних элементов. Настройка резонаторов необходима потому, что в спектре генератора могут присутствовать несколько близких частот. Детекторную секцию настраивают путем вращения контактного поршня 4 и перемещения подвижного поршня 5 (рис. 1.1). Регулировка погружения зонда в волновод производится гайкой 6.

Принцип измерения с помощью измерительной линии основан на возможности определения величины и характера комплексного сопротивления нагрузки по распределению электромагнитного поля вдоль линии.

Для описания процессов, происходящих в волноводах конечной длины (каковой и является измерительная линия), используют теорию длинных линий, которая основана на концепции падающих и отраженных волн. Структура падающей и отраженной волны предполагается такой же, как и в линии бесконечной длины, т. е. напряжение и ток в линии являются функциями только продольной координаты x. Записывается это следующим образом:

Uɺ( x) = Uɺпадe−iγx + Uɺотрeiγx ,

Iɺ( x) = 1 (Uɺпадe−iγx + Uɺотрeiγx ), (1.1)

Z0

4

где Uɺпад и Uɺотр − соответственно комплексные амплитуды падающей и отра-

женной волн; Z0 − волновое сопротивление линии передачи; γ − комплексная постоянная распространения.

Рис. 1.1. Упрощенная схема измерительной линии типа Р1-4:

1 – волновод стандартного сечения со щелью; 2 – внутренний стержень; 3 – внешняя трубка; 4 – контактный поршень; 5 – подвижный поршень;

6 – гайка, регулирующая глубину погружения зонда; 7 – внутренняя трубка; 8 – индикаторный прибор; 9 – ВЧ фильтр; 10 – детектор; 11 − зонд.

Амплитуда падающей волны напряжения Uɺпад определяется мощностью

генератора.

Отношение комплексной амплитуды напряжения отраженной волны Uɺотр к комплексной амплитуде напряжения падающей волны Uɺпад в данном сечении линии x зависит от величины нагрузки, подключенной к концу линии, и называется коэффициентом отражения по напряжению Гɺ( x):

В общем случае коэффициент отражения является комплексной величиной, т. е. Гɺ( x) = Г eiϕ , где φ − фаза коэффициента отражения. Полное сопро-

тивление нагрузки Zɺн (импеданс) и ее проводимость Yɺн (адмиттанс) также имеют комплексный характер:

Zɺн = Rн + jX н ,

Yɺн = Gн + jBн ,

5

где RН и GН − вещественные части сопротивления и проводимости (активное сопротивление и активная проводимость) нагрузки соответственно; Xн и Bн − мнимые части сопротивления и проводимости (реактивное сопротивление и реактивная проводимость соответственно).

Для пассивных нагрузок всегда выполняется условие Г £1. Коэффици-

Если линия передачи не согласована с нагрузкой, т. е. Zɺн ¹ Z0 , то коэф-

фициент отражения в таких случаях будет отличен от нуля, и в линии будут присутствовать две волны – падающая и отраженная. Одновременное существование в линии передачи двух волн, которые в разных точках линии обладают различными фазовыми сдвигами, приводит к тому, что результирующее колебание изменяет свою амплитуду и начальную фазу от точки к точке, т. е. имеет место интерференция падающей и отраженной волн. Интерференция этих двух волн будет создавать в линии периодическую структуру поля, которое будет характеризоваться значением напряжения в пучностях Umax и узлах Umin. Значение напряжения в узлах и пучностях зависит от сопротивления нагрузки и определяется следующим образом:

Umin = Uпад – Uотр ,

Umax = Uпад + Uотр .

Решение практических задач часто требует согласования различных нагрузок с линией передачи. В качестве меры согласования используют коэффициент стоячей волны по напряжению (обозначается КСВН):

Иногда вместо КСВН используют другой коэффициент – коэффициент бегущей волны (КБВ):

6

Определив при помощи измерительной линии один из приведенных выше коэффициентов, можно вычислить модуль коэффициента отражения

|Г |:

Таким образом, модуль коэффициента отражения в линии без потерь, описываемы формулами (1.6), не зависит от значения координаты l и полно-

стью определяется сопротивлением нагрузки Zɺн .

Входное сопротивление нагруженного отрезка линии в произвольной точке продольного сечения зависит от сопротивления нагрузки Zɺн , волнового сопротивления линии Z0 и расстояния от нагрузки до точки измерения l:

где β − коэффициент фазы, который равен мнимой части коэффициента рас-

длина волны в линии. Формула (1.7) также носит название формулы трансформации сопротивления в линии передачи.

Как видно из (1.7), входное сопротивление является периодической функцией с периодом πβ = λ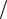2 . Соответственно, пучности и узлы напряже-

ний и, следовательно, токов в линии также чередуются через каждые λ/2. Это означает, что удлинение или укорочение линии на отрезок, кратный λ/2, не сказывается на величине входного сопротивления.

Часто при записи выражения для определения Zɺвх и Zɺн используют нормировку относительно волнового сопротивления линии Z0:

Рассмотрим характер распределения тока и напряжения в идеальной линии без потерь для основных частных случаев нагрузки. Следует иметь в виду, что определение распределения напряжения и тока вдоль линии производят при помощи измерительной линии, в которой происходит преобразование напряжения и тока детекторной головкой. Иначе говоря, измеряются только амплитуды полей токов и напряжений, и, следовательно, их распределения вдоль измерительной линии в этом случае будут однополярными.

7

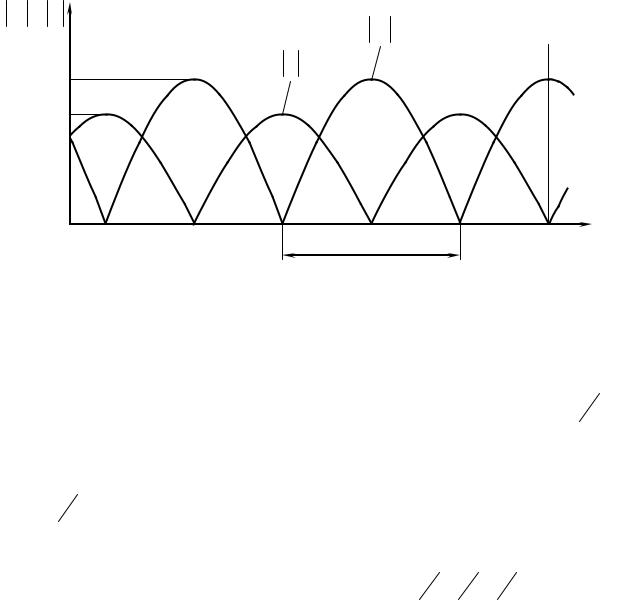
1. Рассмотрим распределение полей токов и напряжений вдоль разомкнутой линии (холостой ход), т. е. Zɺн = ∞ (рис. 1.2). Вертикальной пунктирной линией на рисунке отмечено сечение нагрузки.

U , I

U

Рис. 1.2. Распределение амплитуд напряжений и токов в разомкнутой линии.

Так как линия на конце разомкнута, то в линии устанавливается такой режим, что на конце получается максимальное значение напряжения и нулевое

конца линии образуется узел напряжения и пучность тока. В этом сечении входное сопротивление отрезка равно нулю, а эквивалентная схема может быть представлена последовательным колебательным контуром. На расстоя-

нии l = λ 2 от конца линии ток снова равен нулю, а напряжение максимально.

В этом случае входное сопротивление отрезка становится равным бесконечности, а эквивалентная схема может быть представлена параллельным колеба-

тельным контуром. В промежутках между точками λ 4 , λ 2 , 3 4 λ и т. д. в за-

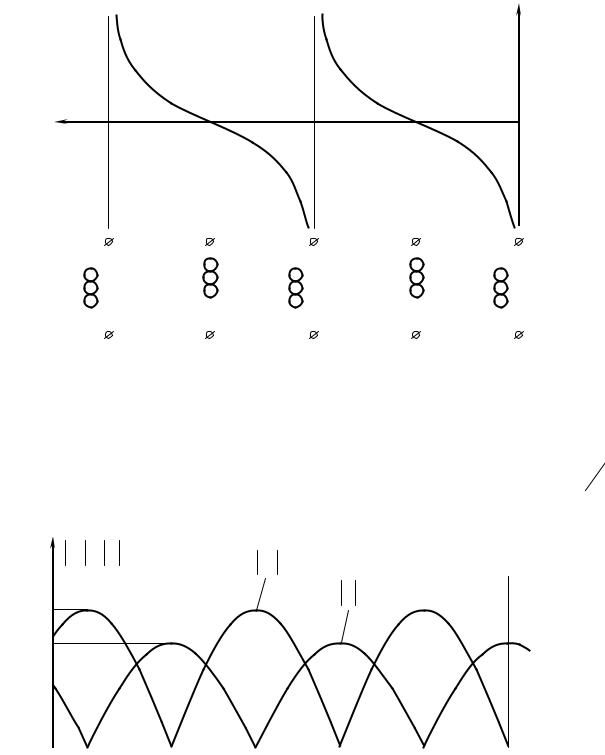
висимости от расстояния до конца линии входное сопротивление линии может иметь емкостной (в диапазоне значений l, где Zɺвх < 0 ) или индуктивный (в диапазоне значений l, где Zɺвх > 0 ) характер (рис. 1.3).

8

Рис. 1.3. Эпюры входного сопротивления для разомкнутой линии.

2. Короткозамкнутая линия ( Zɺн = 0 ).

В этом случае ток на конце линии будет иметь максимальное значение, а напряжение равняться нулю. Распределение тока и напряжения получается

аналогичным случаю холостого хода, только смещенным вдоль линии на λ 4

(рис. 1.4).

0 x

Рис. 1.4. Распределение амплитуд напряжений и токов в короткозамкнутой линии.

3. Линия нагружена на активное сопротивление RН, равное ее волновому

сопротивлению, т. е. Zɺн = Rн = Z0 .

В этом случае линия подобна бесконечно длинной линии. Вся энергия, подводимая к линии, распределяется вдоль нее в виде бегущей волны и полно-

9

стью поглощается в нагрузке на конце линии. Амплитуда напряжения и тока будет постоянна по всей линии (рис. 1.5).

U , I

U

Zɺн = Z0

Uпад

Iпад

I

0 x

Рис. 1.5. Распределение амплитуд напряжений и токов в согласованной линии.

4. Линия нагружена на чисто активное сопротивление, не равное ее волновому сопротивлению, т. е. Zɺн = Rн ¹ Z0 .

В этом случае часть энергии отражается от нагрузки, и в линии будет присутствовать и падающая, и отраженная волны. Величина и положение максимума и минимума определяется соотношением между волновым сопротив-

лением линии и сопротивлением нагрузки. При Zɺн < Z0 распределение напряжения и тока будут напоминать случай короткого замыкания. Особенно это будет заметно при Zɺн Z0 . На конце линии будет наблюдаться максимум тока и минимум напряжения (рис. 1.6).

0 x

Рис. 1.6. Распределения амплитуд напряжений и токов вдоль линии, нагруженной на чисто активное сопротивление, гораздо меньшее волнового сопротивления линии.

При Zɺн > Z0 распределение напряжения будет несколько напоминать

распределение напряжения при холостом ходе, т. е. на конце линии будет наблюдаться максимум напряжения и минимум тока. Особенно это будет замет-

но при значениях Zɺн Z0 (рис. 1.7).

10