II. Дифференциальное исчисление функций нескольких переменных

§ 1. Функции нескольких переменных. Основные понятия.

Область существования. Линии и поверхности уровня

Чтобы изобразить на плоском рисунке поверхность, заданную функцией двух переменных , используют так называемыелинии уровня, которые задаются уравнением где. Этот способ заключается в следующем: сначала строят сечения поверхности горизонтальными плоскостями , а затем наносят полученные кривые на плоскость. На географических картах таким способом изображают рельеф местности.

Поверхности уровня функции представляют собой геометрическое место точек пространства, в которых данная функция принимает одно и то же значение

.

Определение (Функция многих переменных). Если каждой точке из множестваточек-мерного евклидова пространстваставится в соответствие по известному закону некоторое числото говорят, что на множествезадана функция, или. При этом множествоназывается областью задания функции

Число соответствующее данной точкеиз множества, называютчастным значением функции в точке . Совокупность всех частных значений функцииназываютмножеством значений этой функции. Так как точка определяется своими координатами то для функции переменныхиспользуется еще одно обозначение

Пример 1.1. Найти область значений функции

Решение. Областью задания этой функции является круг радиусом 1 с центром в начале координат, а множество значений представляет собой отрезок

Пример 1.2. Найти область определения функции

.

Решение. Эта функция определена для всех троек , удовлетворяющих одновременно условиям

Пример 1.3. Найти линии уровня функции .

Решение. На основе определения линий уровня запишем

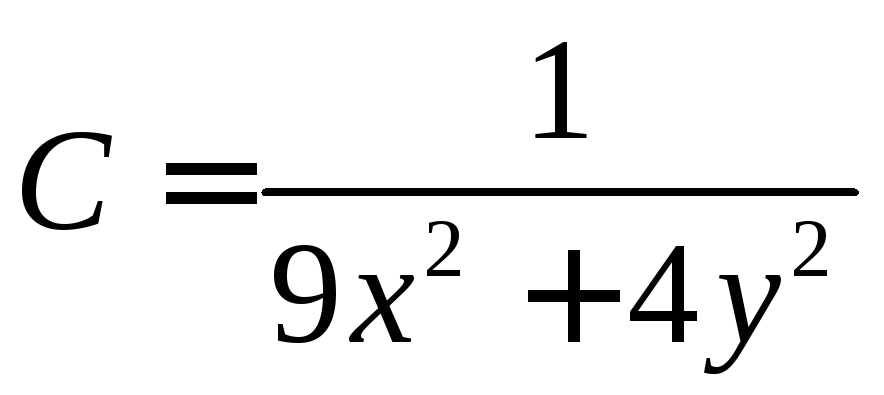, или . Преобразуем это выражение:

.

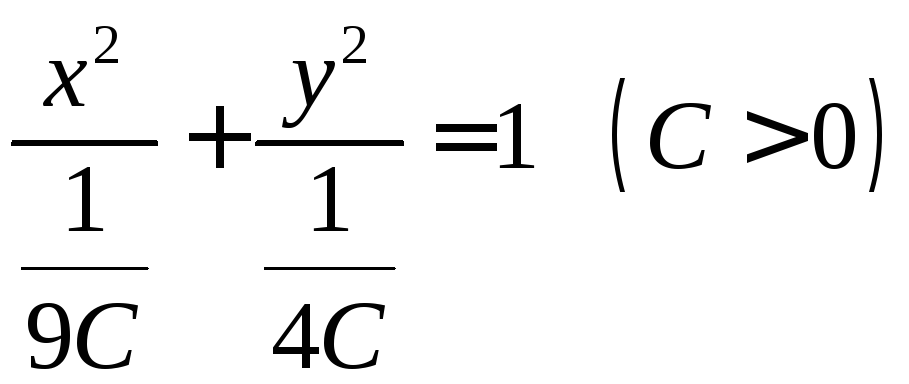Таким образом, линии уровня заданной функции являются эллип-сами.

Пример 1.4. Найти поверхности уровня функции .

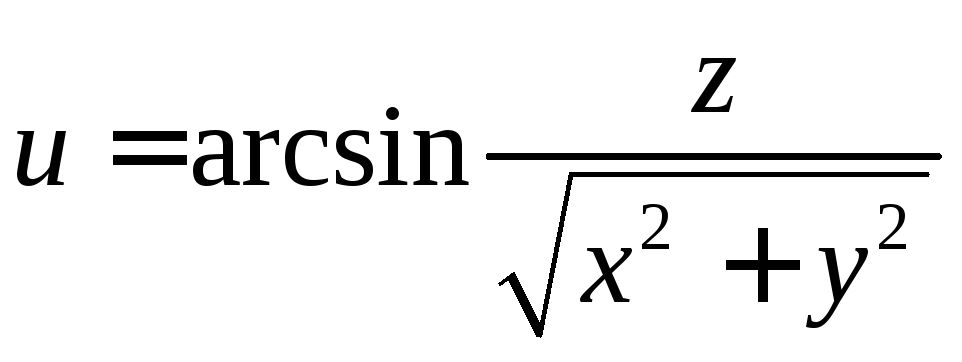Решение. Запишем уравнение поверхности уровня

.

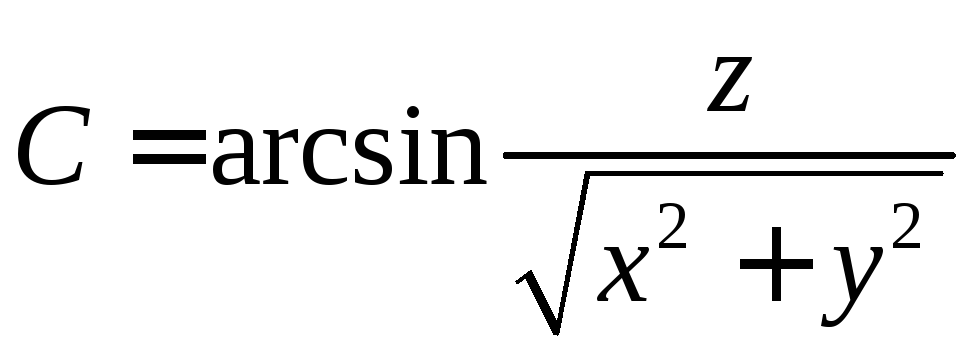Преобразуем это уравнение:

.

Тогда поверхностями уровня будет семейство конусов

.

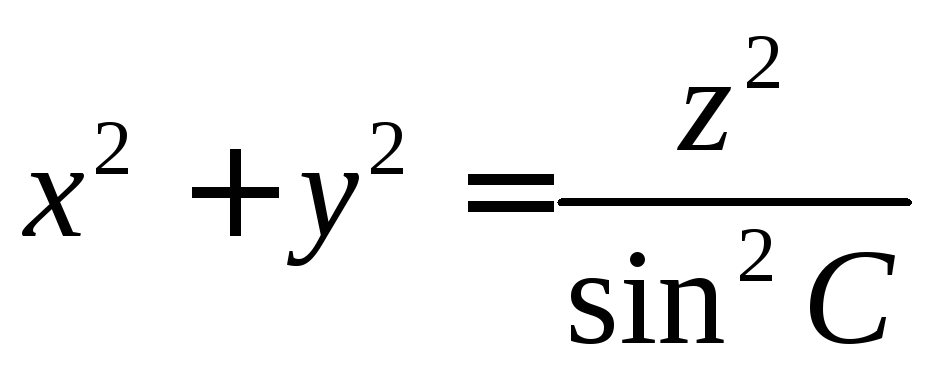Сделав замену , получим

,

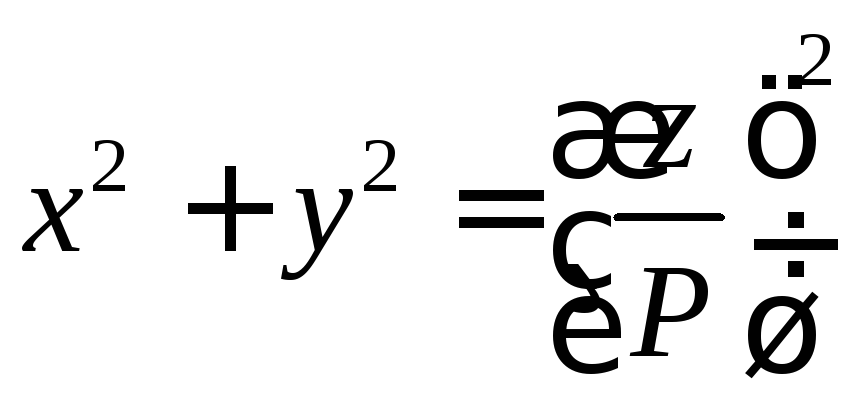где .

Определить и изобразить области существования следующих функций:

1.1. .	1.2. .
1.3. .1.3. .	1.4. .
1.5. .	1.6. .

Построить линии уровня следующих функций:

1.7. .
1.8. а) ;	б) ;
в) ;	г) .
1.9. .	1.10. .

Построить поверхности уровня следующих функций:

1.11. .

1.12. .

Ответы: 1.1. Все точки плоскости вне круга .1.2. Кольцо .1.3. Пара вертикальных углов .1.4. Совокупность четырех октантов пространства. 1.5. Открытая пирамида с вершинами в точках .1.6. Внутренность двуполостного гиперболоида . 1.7. Семейство подобных эллипсов. 1.8. а) I и III квадранты при , семейство двухзвенных ломаных линий, звенья которых параллельны осям координат, а вершины расположены на прямойпри; б) линии уровня – стороны углов, параллельные положительным направлениям координатных осейи, с вершинами на прямой; в) семейство контуров квадратов с общим центром, стороны которых параллельны осям координатипри, точкапри; г) прямые, параллельные оси, если, стороны углов, параллельные координатной осии положительной полуоси, с вершинами на параболе, если, положительная полуось, если.1.9. Пучок окружностей, проходящих через начало координат (не включая этого начала) и ортогональных к оси .1.10. Семейство окружностей, ортогональных к оси и проходящих через точки, за вычетом последних.1.11. Семейство двуполостных гиперболоидов при , семейство однополостных гиперболоидов при, конус при.1.12. Семейство концентрических сфер при , семейство сферических слоев , где , приили.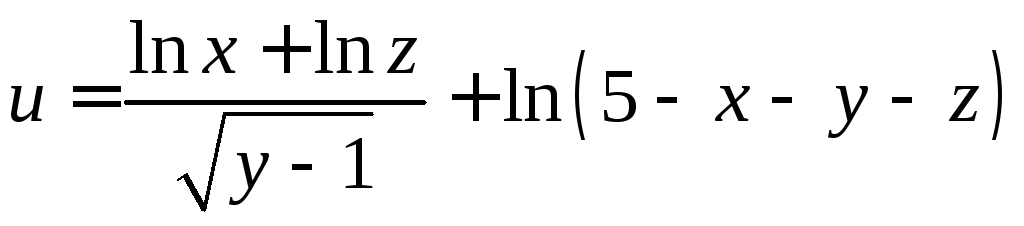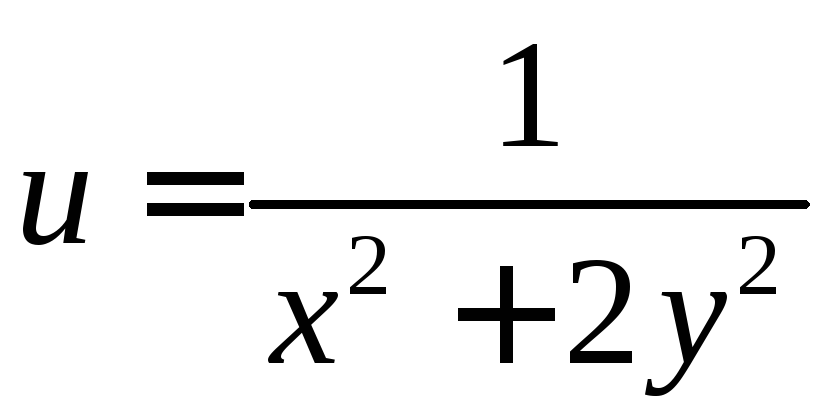