§ 3. Частные производные и полный дифференциал функции нескольких переменных

Определение 3.1. Если существует предел отношения частного приращенияфункции в точкек соответствующему приращениюаргументаприто этот предел называетсячастной производной функции в точкепо аргументу:

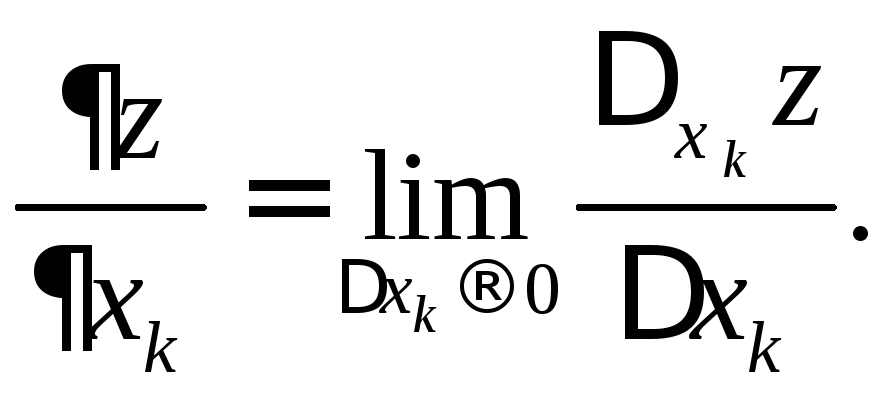
Для частных производных общеприняты следующие обозначения: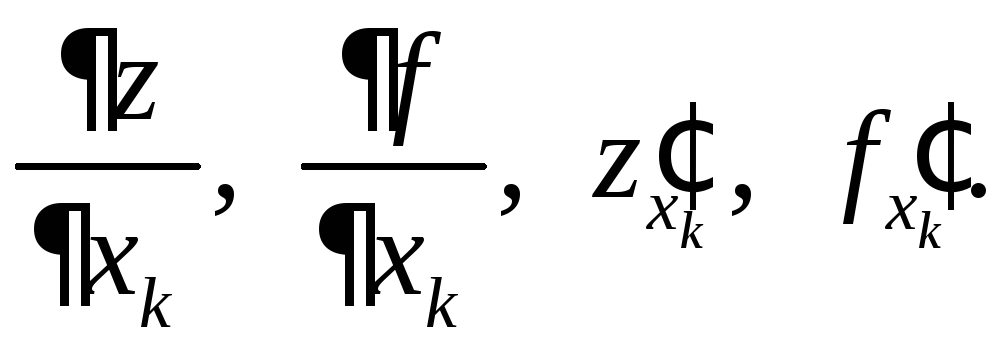

Из определения следует простой практический метод отыскания частных производных: когда мы вычисляем производную функции по какой-нибудь одной переменной, то все остальные при этом считаем константами. Что касается правил вычисления, то они не отличаются от таковых для функций одной переменной.

Определение 3.2. Дифференциалом дифференцируемой в точкефункции называется главная линейная относительно приращений аргументов часть приращения функции в точке. Если все коэффициентыв представленииприращения дифференцируемой функции равны нулю, то дифференциалфункции в точке М считается равным нулю.

Таким образом, дифференциалом дифференцируемой в точкефункции называется выражение

или

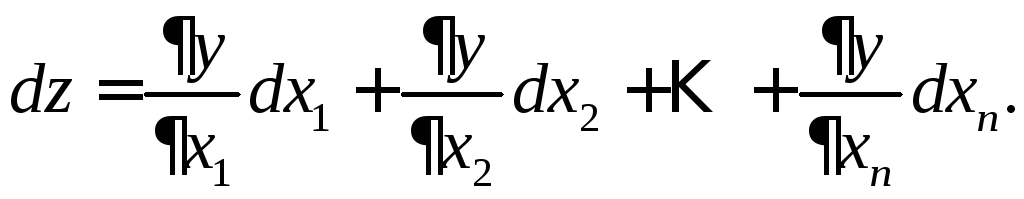
Пусть частная производная по аргументуфункции, определенной в областисуществует в каждой точкеобласти. В этом случае указанная частная производная представляет собой функцию переменныхтакже определенную в области. Если эта функцияимеет частную производную по аргументув некоторой точкеобласти, то ее называют второй частной производной, или частной производной второго порядка функциив точкесначала по аргументуа затем по аргументуи обозначают одним из следующих символов:

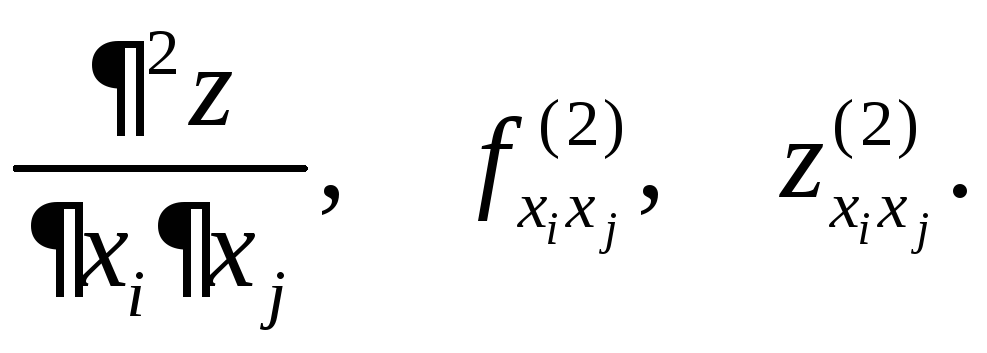
При этом если то частную производнуюназывают смешанной частной производной второго порядка. Аналогично понятию второй частной производной, можно последовательно ввести понятие третьей частной производной, затем четвертой и т. д.

Так как частная производная функции по аргументу определяется как обыкновенная производная функции одной переменнойпри фиксированных значениях остальных переменных, то методика вычисления частных производных высших порядков предполагает умение вычислять только обыкновенные производные первого порядка.

Принцип, по которому мы находили частные производные высших порядков, мы можем применить к нахождению дифференциалов высших порядков:

Для независимых переменных справедливы следующие формулы:

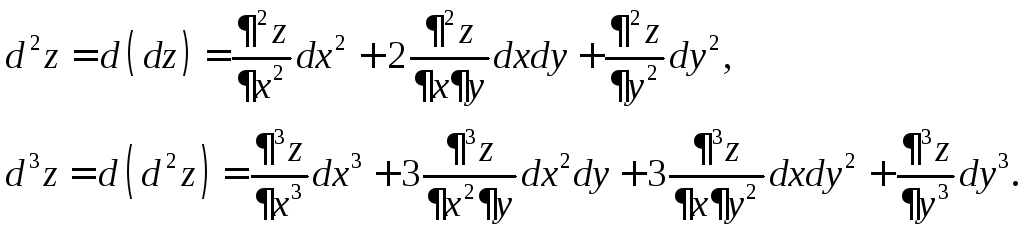
В общем случае удобна операторная запись для дифференциала -го порядка

Это выражение также справедливо только в случае независимых переменных.

Приближенные вычисления. Если функция дифференцируема в точке, то можно приближенно заменить приращение функции в этой точке ее дифференциалом. Тогда

Если в этой формуле положить , то получим формулу для приближенных вычислений

Пример 3.1. Найти частные производные 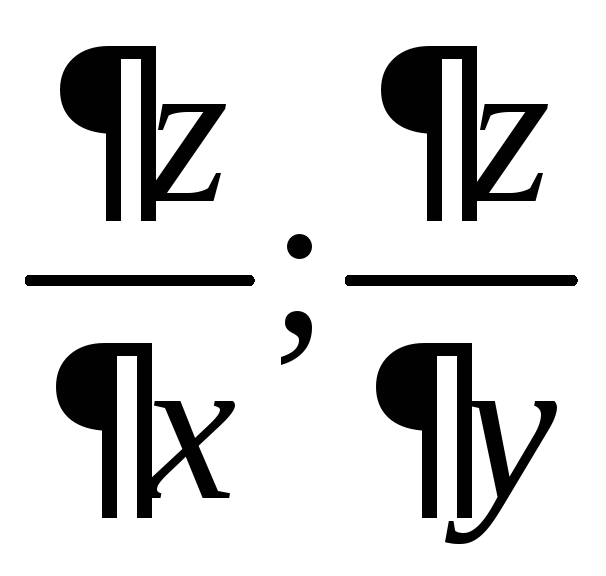функции

.

Решение. Найдем частную производную вначале по переменной , считая другую переменнуюконстантой:

.

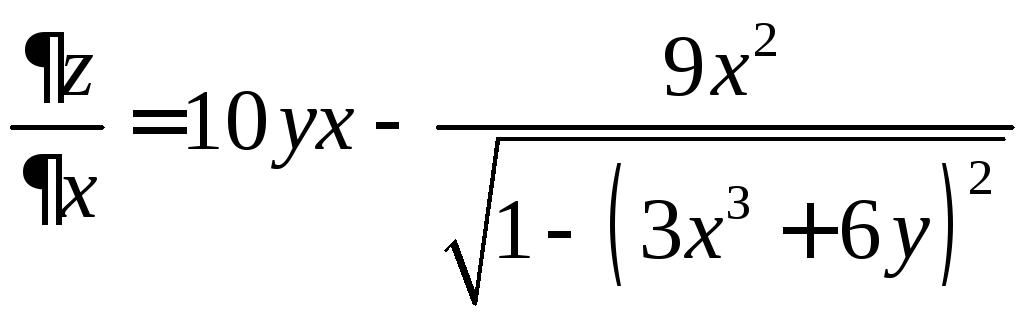Затем продифференцируем функцию по другой переменной, а будем считать константой:

.

Пример 3.2. Найти частные производные 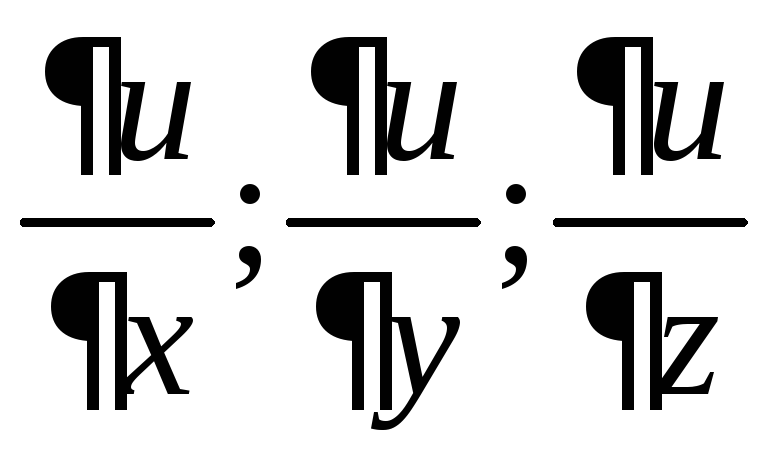функции трех переменных

.

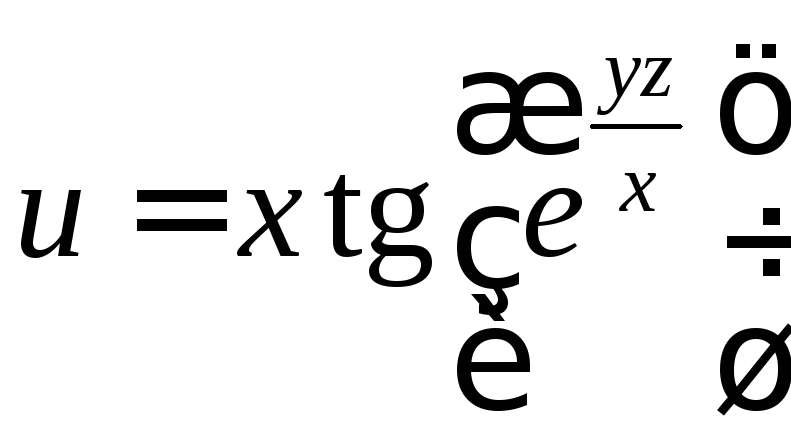Решение. Используя тот же принцип, что и в предыдущем примере, найдем последовательно все частные производные:

;

; .
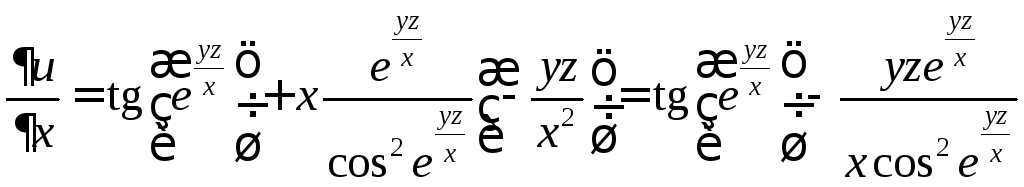
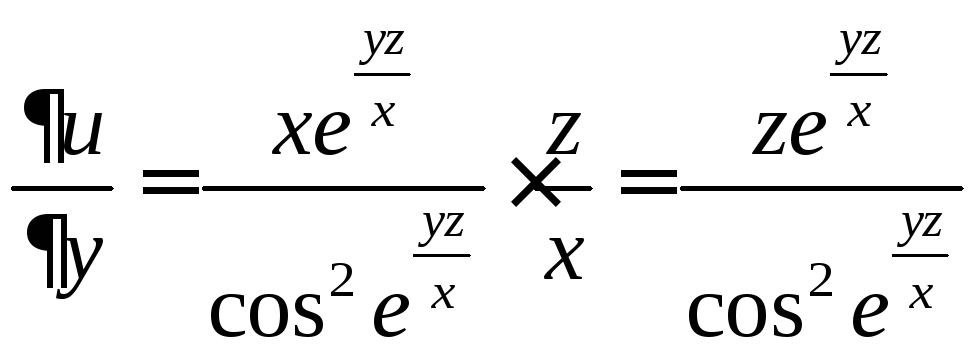
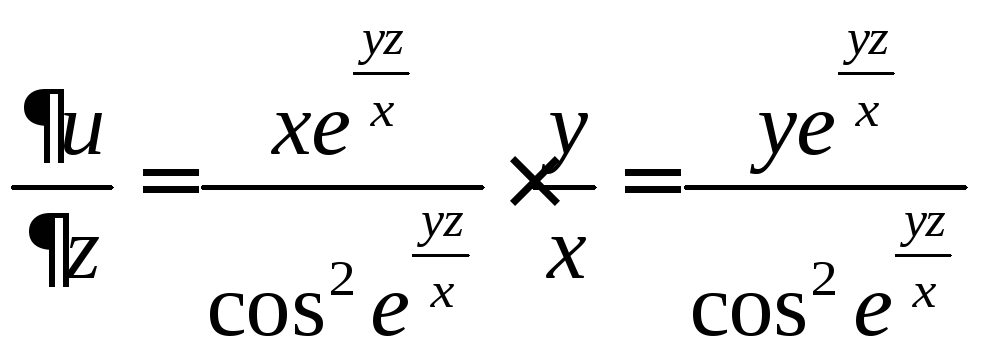