§ 2. Предел и непрерывность функции нескольких переменных

Рассмотрим функцию определенную на множестветочек-мерного евклидова пространстваи точкупространства, быть может и не принадлежащую множествуно обладающую тем свойством, что в любой-окрестности этой точкисодержится хотя бы одна точка множестваотличная от. Расстояние между точкамииобозначим.

Определение 2.1 (Предел функции в точке по Гейне). Число называется пределом функциив точке, если для любой сходящейся кпоследовательноститочек множества, все элементыкоторой отличны от, соответствующая числовая последовательность значений функциисходится к числу

Определение 2.2 (Предел функции в точке по Коши). Число называется пределом функцииприесли для любого положительного числанайдется отвечающее ему положительное числотакое, что для любой точкииз множества, удовлетворяющей условиюсправедливо неравенство.

Для обозначения предела функции в точкепринято использовать следующие символы:

,

где – координаты точки.

Понятие непрерывности функции переменных также имеет два определения.

Рассмотрим функцию переменных, заданную на некотором множествепространства . Пусть – некоторая точка принадлежащая множеству , такая, что в любой-окрестности точкисодержатся точки множестваотличные от.

Определение 2.3. Функция называется непрерывной в точке, если предел функции в точкесуществует и равен частному значению

Точки пространства , в которых функция не обладает свойством непрерывности, называютсяточками разрыва этой функции.

На основе определений предела функции в точке по Гейне и по Коши мы можем сформулировать определения непрерывности функций в данной точке по Гейне и по Коши.

Определение 2.4 (Непрерывность функции точке по Гейне). Функция называется непрерывной в точке, если для любой сходящейся кпоследовательноститочек множествасоответствующая числовая последовательностьзначений функции сходится к числу

Определение 2.5 (Непрерывность функции в точке по Коши). Функция называется непрерывной в точке, если для любого положительного числанайдется отвечающее ему положительное числотакое, что для любой точкииз множества, удовлетворяющей условиюсправедливо неравенство

Дадим определение непрерывности функции на множестве.

Определение 2.6. Функция , определенная на множестве, называется непрерывной на этом множестве, если она непрерывна в каждой точкеэтого множества.

Определение 2.7 (Равномерная непрерывность функции на множестве). Функция , определенная на множестве, называетсяравномерно непрерывной на этом множестве, если для любого существует такое, что для любых двух точекмножества, расстояние между которыми удовлетворяет условию, выполняется неравенство

.

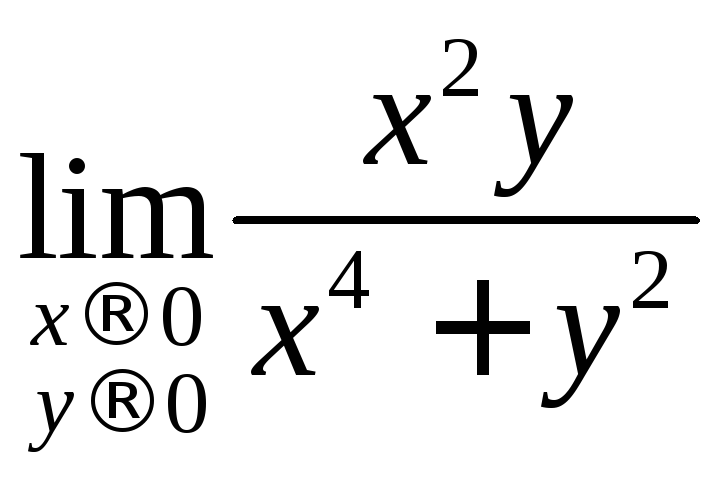Пример 2.1. Найти предел функции в точкепо прямой; доказать, чтоне существует.

Решение. Функция определена во всех точках плоскости, кроме точки . Так как

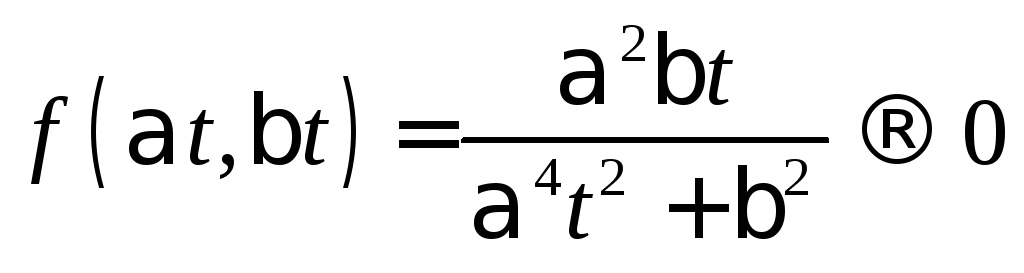
при (если, то), то предел функции в точке по каждой прямой, проходящей через начало координат, равен нулю.

Чтобы доказать, что 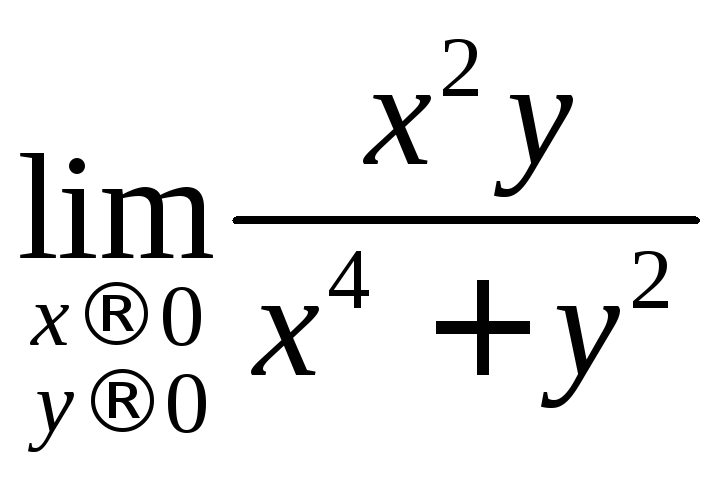не существует, достаточно указать кривую, проходящую через начало координат, по которой предел функции в точкене равен нулю. Такой кривой является, например, парабола. Действительно,и.

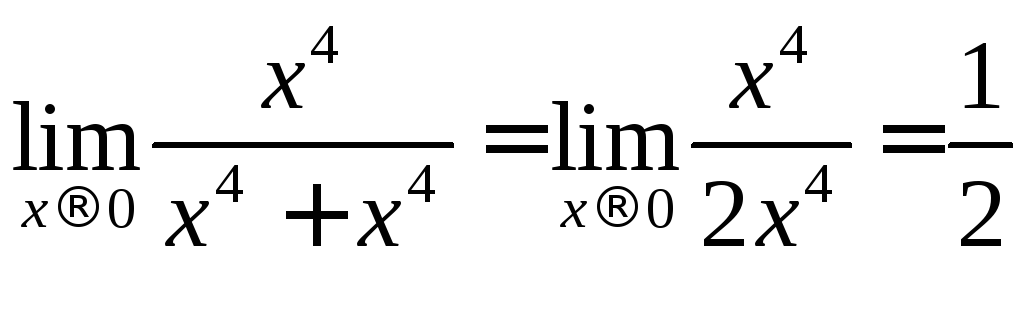Пример 2.2. Исследовать на непрерывность функцию

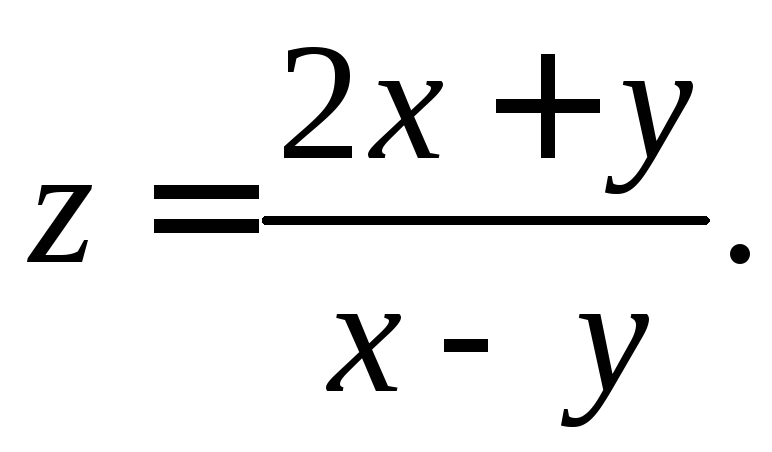
Решение. Функция не определена во всех точках, для которых . Следовательно, она терпит разрыв в точках, лежащих на этой прямой.

Пример 2.3. Исследовать на равномерную непрерывность функцию .

Решение. Функция непрерывна на множестве рациональных точек плоскости. Однако она не является равномерно непрерывной, так как разность значений функции в точках и, где, будет больше любого числа, если, как бы мало ни было расстояниемежду точками.

2.1. Показать, что для функции 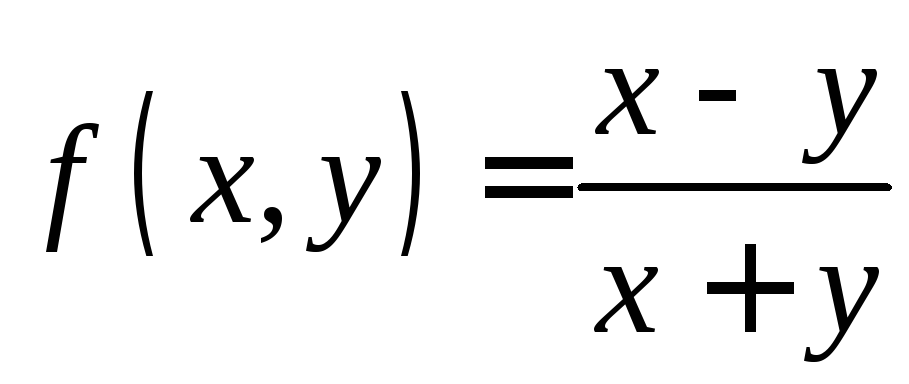имеются повторные пределы, ноне существует.

2.2. Показать, что для функции 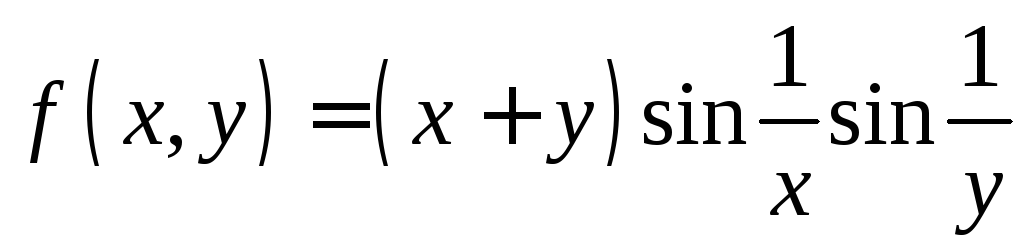оба повторных пределане существуют, но существует.

2.3. Найти , если

а) ;	б) ;
в) ;	г) ;
д) .

Найти следующие двойные пределы:

2.4. .	2.5. .
2.6. .	2.7. .

2.8. Определите, по каким направлениям существует конечный предел:

а) ;

б) ,

если .

Найти точки разрыва следующих функций:

2.9. .	2.10. .
2.11. .

2.12. Показать, что функция

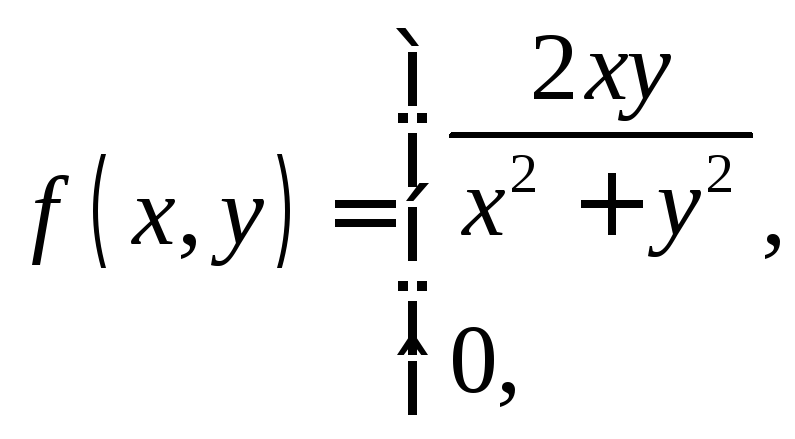
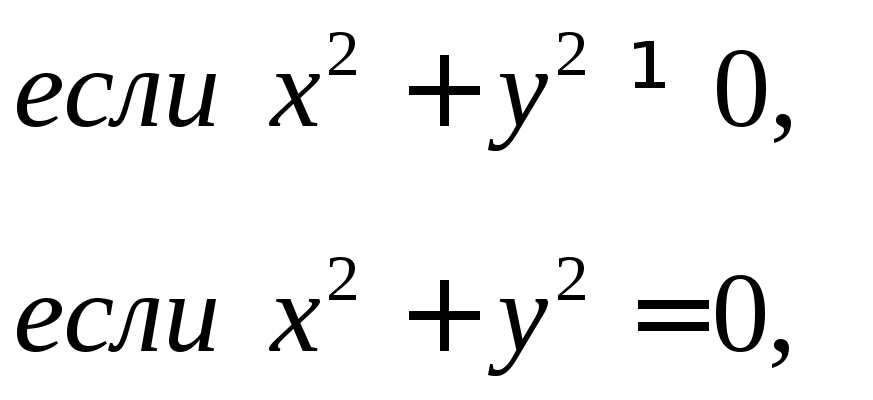
непрерывна по каждой переменной ив отдельности, но не является непрерывной по совокупности этих переменных.

2.13. Найти значение , при котором функция

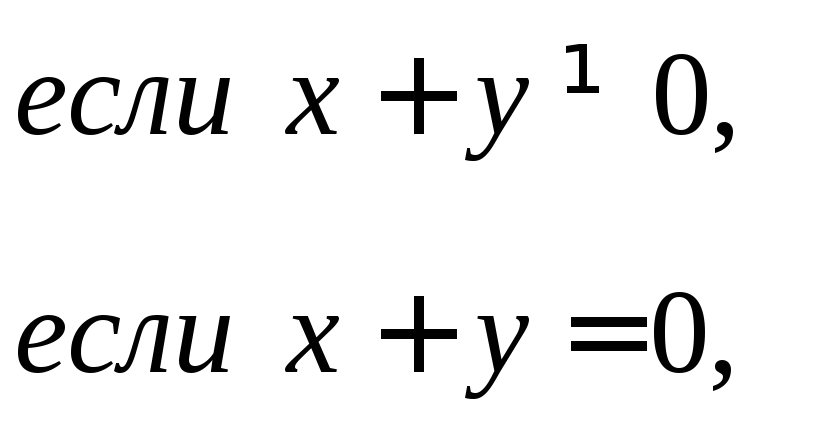
является непрерывной в .

Исследовать на равномерную непрерывность следующие функции на множестве :

2.14. .

2.15. .

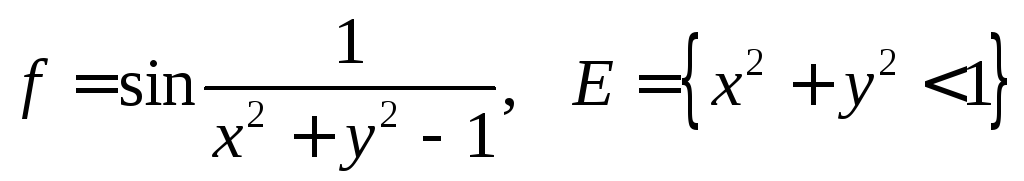2.16. .

2.17. Найти образ окружности при отображении:

1) ;

2) .

2.18. Найти образ прямой при отображении:

.

Ответы: 2.3. а) 0, 1; б) , 1; в) 0, 1; г) 0, 1; д) 1,. 2.4. 0. 2.5. .2.6. 0. 2.7. .2.8. а) ; б) и.2.9. Все точки прямой .2.10. – точка бесконечного разрыва; точки прямой– устранимые точки разрыва.2.11. Точки координатных плоскостей .2.13. 0. 2.14. Равномерно непрерывна 2.15. Не является равномерно непрерывной. 2.16. Не является равномерно непрерывной; 2.17. Эллипс 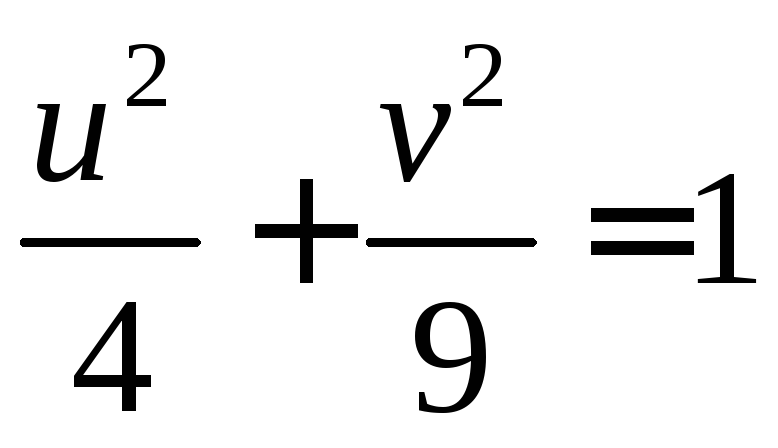;2.18. Цилиндр , если; ось, если.
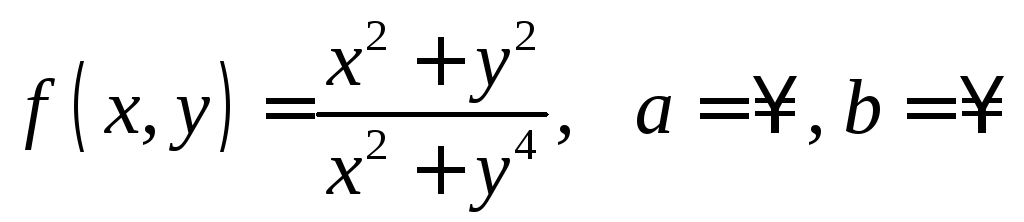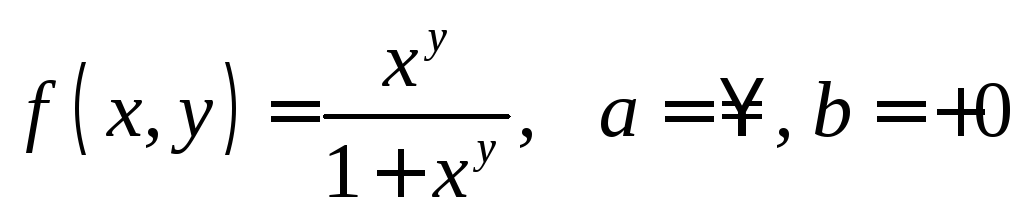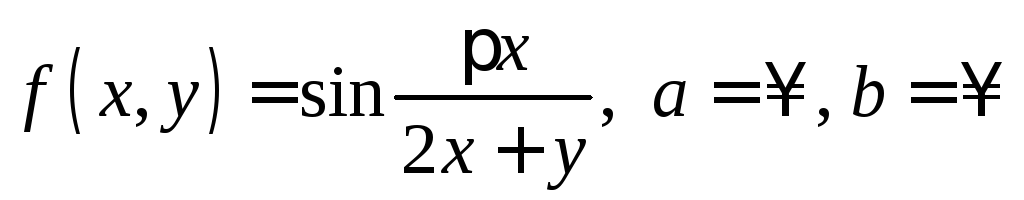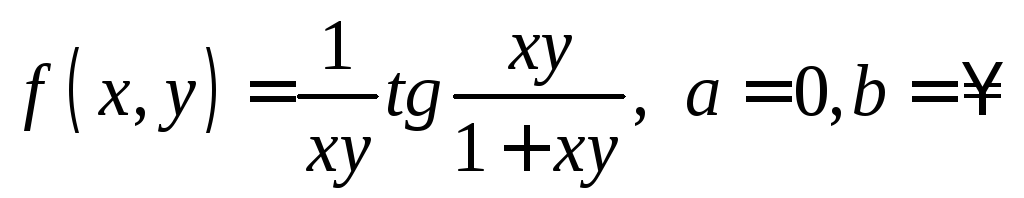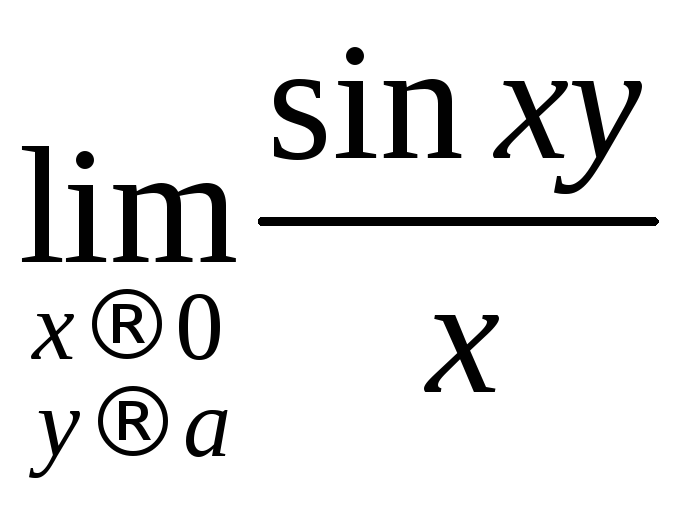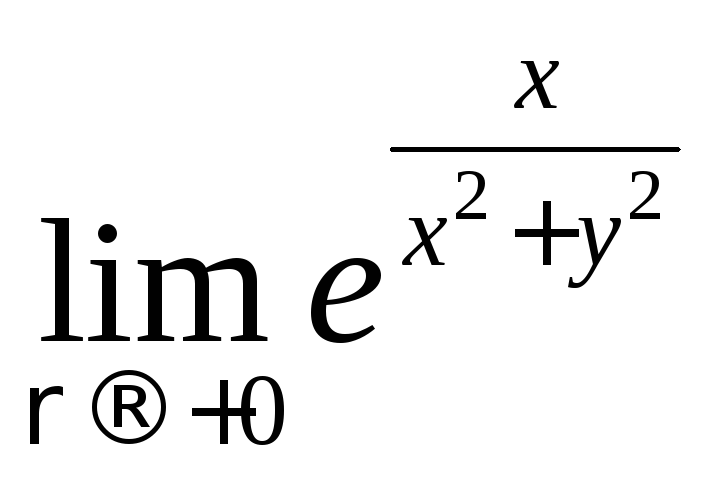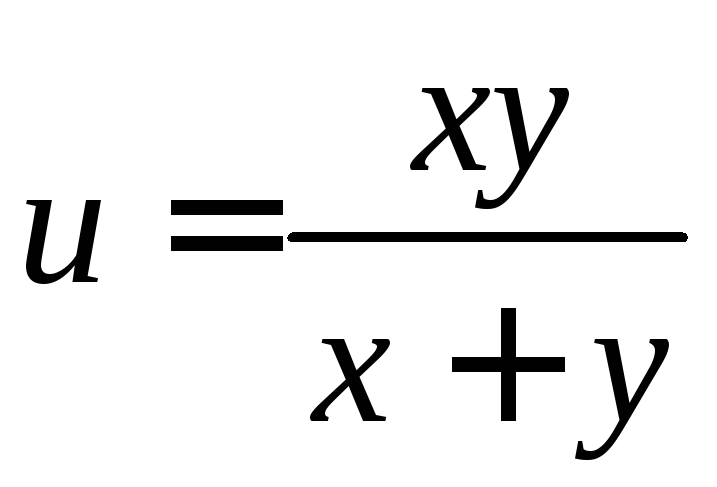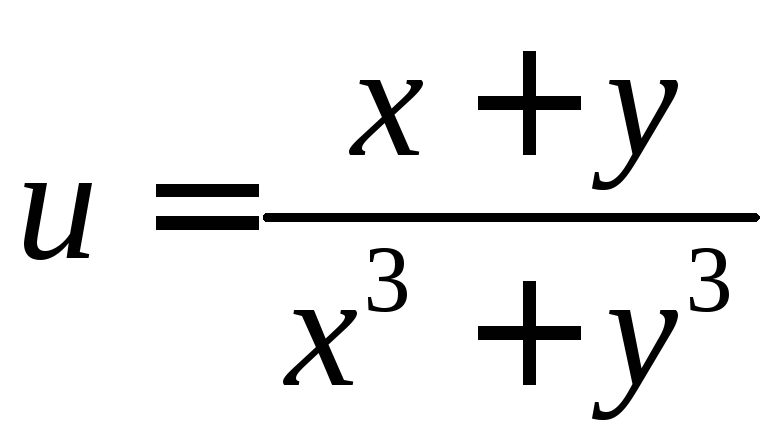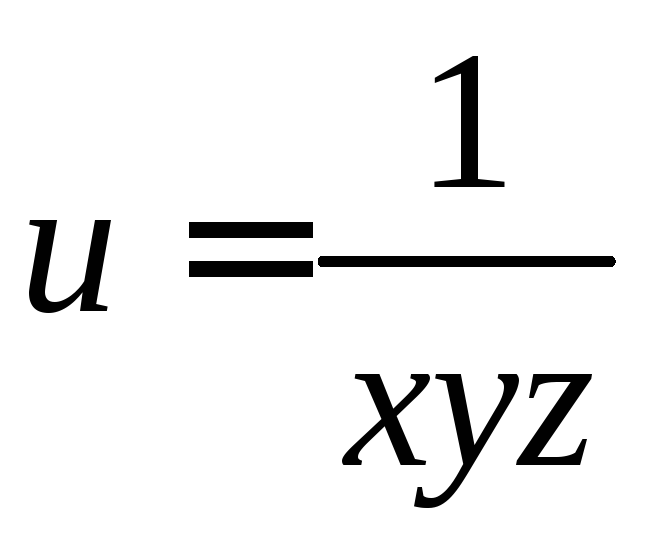