
- •II. Дифференциальное исчисление функций нескольких переменных
- •§ 1. Функции нескольких переменных. Основные понятия.
- •Область существования. Линии и поверхности уровня
- •§ 2. Предел и непрерывность функции нескольких переменных
- •§ 3. Частные производные и полный дифференциал функции нескольких переменных
- •Пример 3.3. Найти полный дифференциал функции в точке .
- •§ 4. Производная сложной функции
- •§ 5. Производная по направлению. Градиент
- •Пример 5.1. Для функции найти градиент и производную по направлению векторав точке.
- •§ 6. Дифференцирование неявных функций
- •§ 7. Замена переменных
- •§ 8. Геометрические приложения
- •§ 9. Формула Тейлора и ряд Тейлора
- •§ 10. Экстремум функции нескольких переменных
§ 5. Производная по направлению. Градиент
Производная по
направлению некоторого вектора
![]() характеризует скорость изменения
функции
характеризует скорость изменения
функции![]() в точке
в точке![]() вдоль этого вектора.
вдоль этого вектора.
Если функция
![]() имеет в точке
имеет в точке![]() непрерывные частные производные, то в
этой точке существует производная
непрерывные частные производные, то в
этой точке существует производная![]() по направлению
по направлению
![]() ,
где
,
где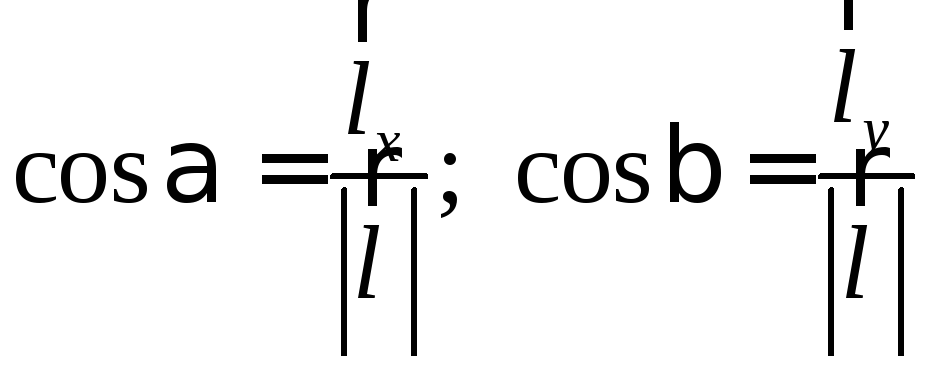 ;
;![]() – длина вектора
– длина вектора![]() ,
причем
,
причем
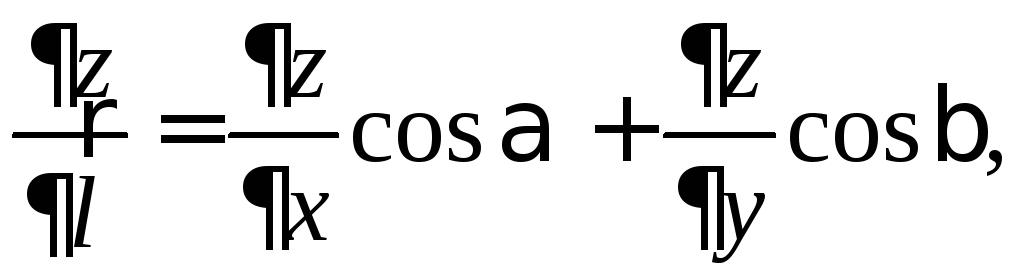
где значения
частных производных ![]() ,
,
![]() вычисляются в
точке
вычисляются в
точке
![]() .
.
Вектор с координатами
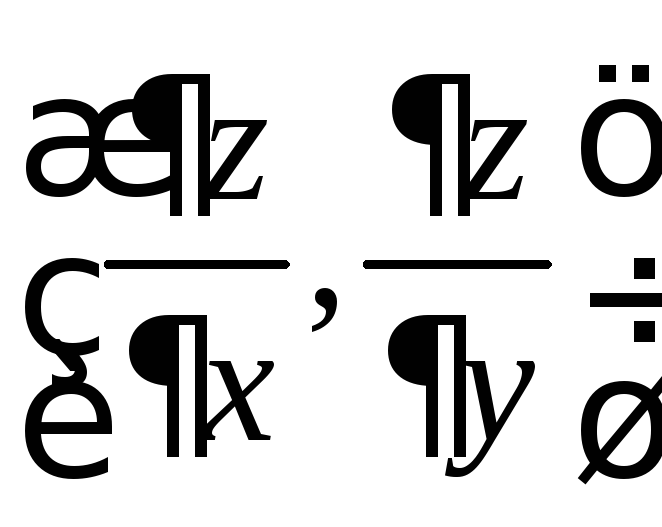 ,
характеризующий направление максимального
роста функции в точке
,
характеризующий направление максимального
роста функции в точке![]() ,
называютградиентом
функции в этой точке и обозначают
,
называютградиентом
функции в этой точке и обозначают
![]() .
.
Производная по направлению и градиент связаны соотношением
![]()
Для функции трех
переменных
![]() направление
направление![]() задается вектором
задается вектором![]() ,
где
,
где![]() – углы между вектором
– углы между вектором![]() и положительными направлениями осей
и положительными направлениями осей![]() ,
,![]() ,
,![]() ,
а
,
а![]() называют направляющими косинусами
вектора
называют направляющими косинусами
вектора
![]() .
.
Тогда
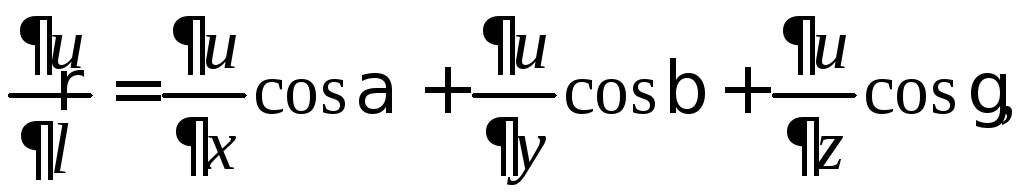
где
![]() есть вектор с координатами
есть вектор с координатами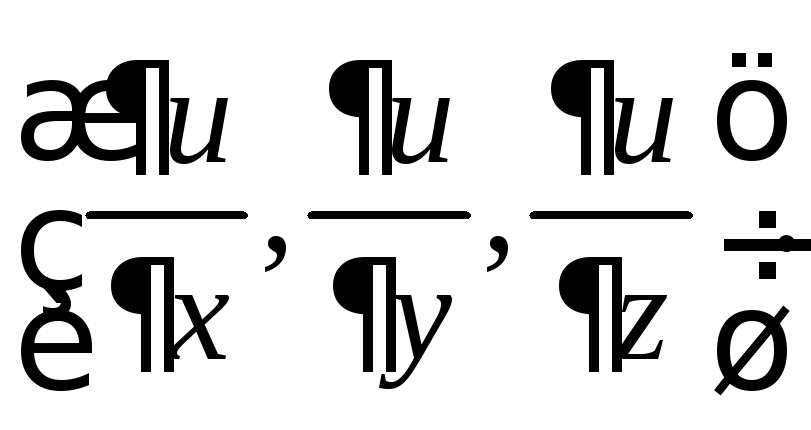
Пример 5.1. Для функции найти градиент и производную по направлению векторав точке.
Решение.
Найдем координаты вектора![]()
![]() в точке
в точке
![]() согласно определению
согласно определению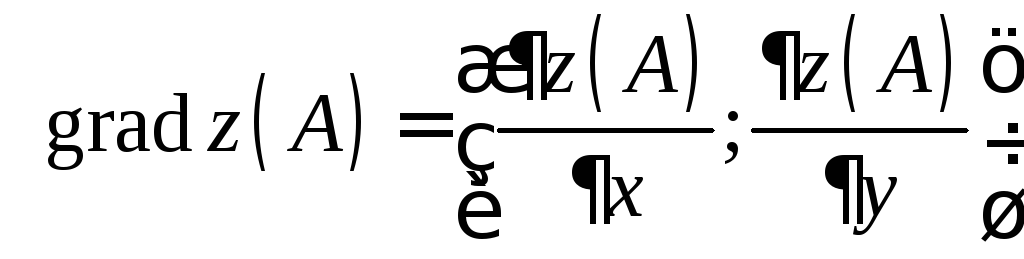 .
.
Вычислим частные
производные и найдем их значения в точке
![]() :
:
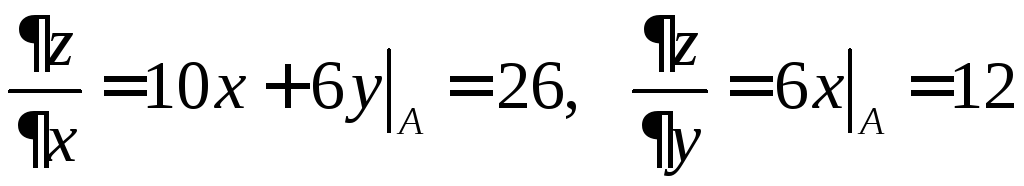 .
.
Таким образом,
![]() .
.
Длину вектора
![]() определим
по формуле
определим
по формуле
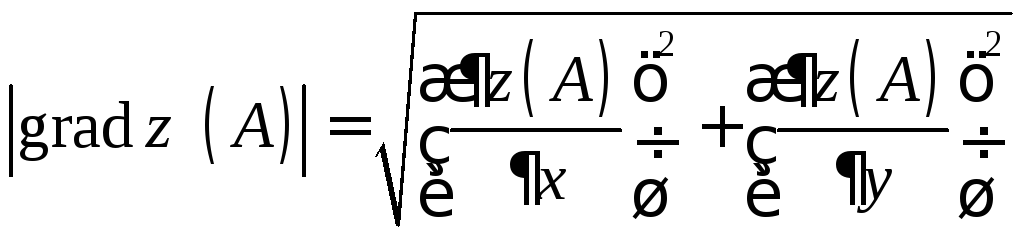 ,
,
Тогда, учитывая найденные координаты вектора, получим
![]() .
.
Далее найдем
производную в точке
![]() по направлению вектора
по направлению вектора
![]() .
Как известно,
.
Как известно,
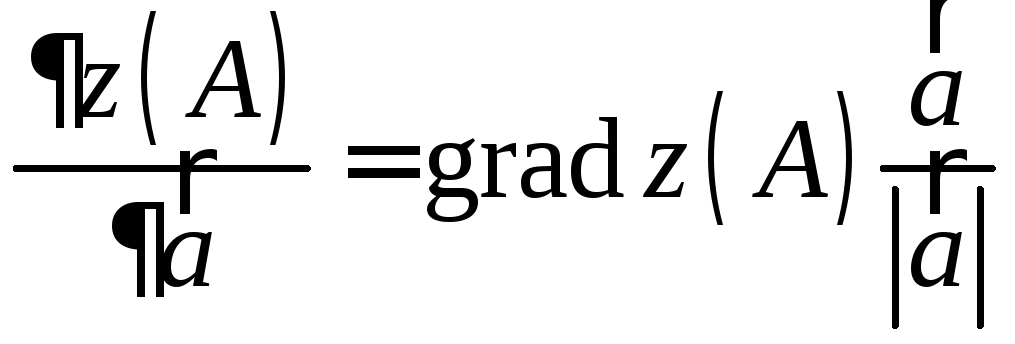 ,
,
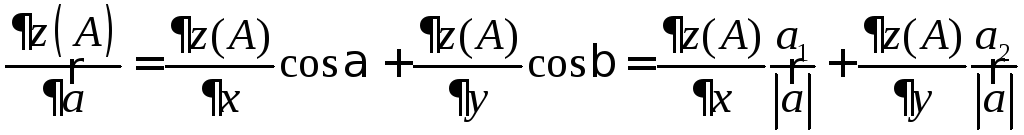 ,
,
где
![]() .
.
Тогда производная
по направлению вектора
![]() в точке
в точке![]() равна
равна
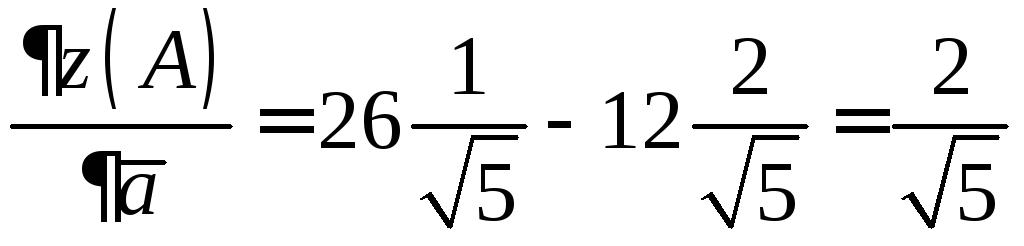 .
.
5.1.
Верно ли следующее утверждение: градиентом
функции
![]() в точке
в точке![]() является вектор
является вектор![]() ?
?
Найти производную
функции
![]() по направлению вектора
по направлению вектора![]() в точке
в точке![]() ,
если:
,
если:
5.2.
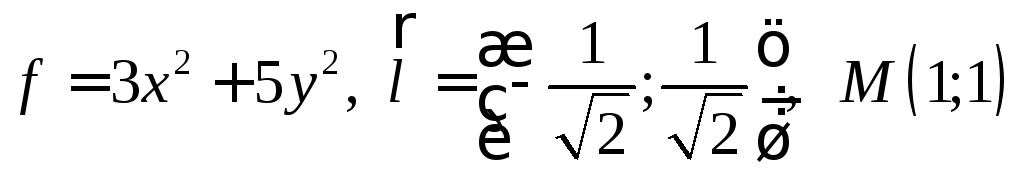 .
.
5.3.
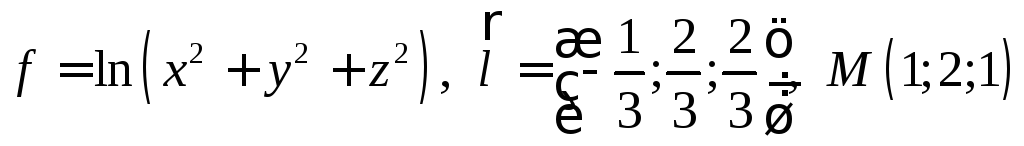 .
.
Найти производную
функции
![]() в точке
в точке![]() по направлению вектора
по направлению вектора![]() ,
если:
,
если:
5.4.
![]() .
.
5.5.
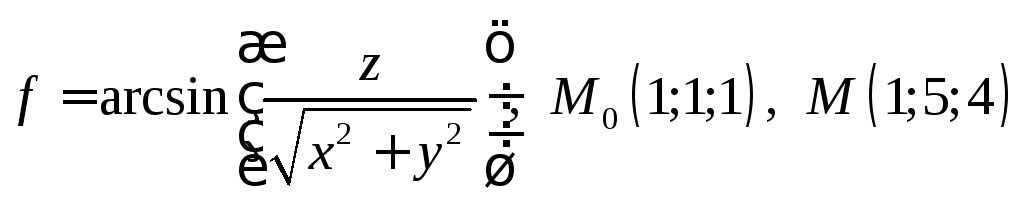 .
.
5.6.
Показать, что в точке
![]() угол между градиентами функций
угол между градиентами функций
![]()
и
![]() ,
,
где
![]() – константы, а
– константы, а![]() стремится к нулю, если точка
стремится к нулю, если точка![]() удаляется в бесконечность.
удаляется в бесконечность.
5.7.
Решить уравнение
![]() ,
если
,
если
![]() .
.
5.8.
Найти наибольшее значение производной
![]() в точке
в точке
![]() ,
если
,
если
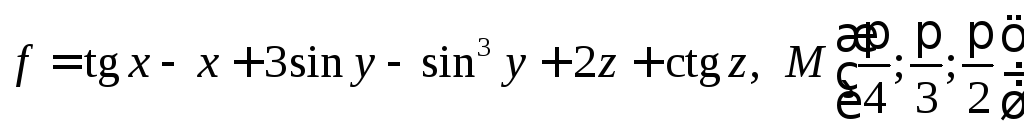 .
.
Ответы: 5.1.
Неверно. 5.2.
![]() .
5.3.
.
5.3.
![]() .
5.4.
.
5.4.
![]() .
5.5.
.
5.5.
![]() .5.7.
.5.7. ![]() ,
,
![]() ,
,
![]() .
5.8.
.
5.8.
![]() .
.
§ 6. Дифференцирование неявных функций
Теорема существования. Если:
1) функция
![]() обращается в нуль в некоторой точке
обращается в нуль в некоторой точке![]() ;
;
2)
![]() и
и![]() определены и непрерывны в окрестности
точки
определены и непрерывны в окрестности
точки![]() ;
;
3)
![]() ,
,
то в некоторой
достаточно малой окрестности точки
![]() существует единственная однозначная
непрерывная функция
существует единственная однозначная
непрерывная функция
![]() ,
,
удовлетворяющая уравнению
![]()
и такая, что
![]() .
.
Частные
производные функций, заданных неявно.
Если выполнены все условия приведенной
выше теоремы и, кроме того, функция
![]() дифференцируема в окрестности точки
дифференцируема в окрестности точки![]() ,
то функция
,
то функция![]() дифференцируема в окрестности точки
дифференцируема в окрестности точки![]() и ее производные
и ее производные![]() и
и![]() могут быть найдены из уравнений
могут быть найдены из уравнений
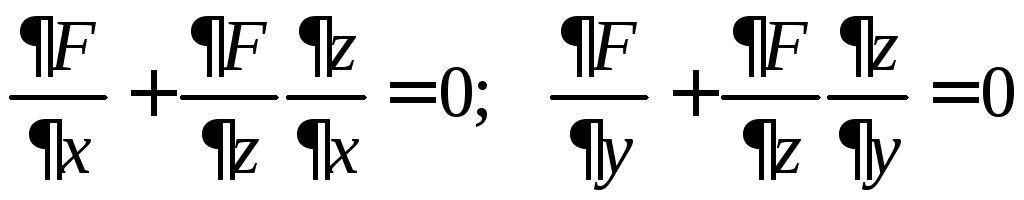 .
.
Если функция
![]() дифференцируема достаточное число раз,
то последовательным дифференцированием
этих уравнений вычисляются производные
высших порядков от функции
дифференцируема достаточное число раз,
то последовательным дифференцированием
этих уравнений вычисляются производные
высших порядков от функции![]() .
.
Дифференцирование
неявных функций, заданных системой
уравнений.
Пусть функции
![]() удовлетворяют следующим условиям:
удовлетворяют следующим условиям:
1) обращаются в
нуль в точке
![]() ;
;
2) дифференцируемы
в окрестности точки
![]() ;
;
3) функциональный
определитель (якобиан)
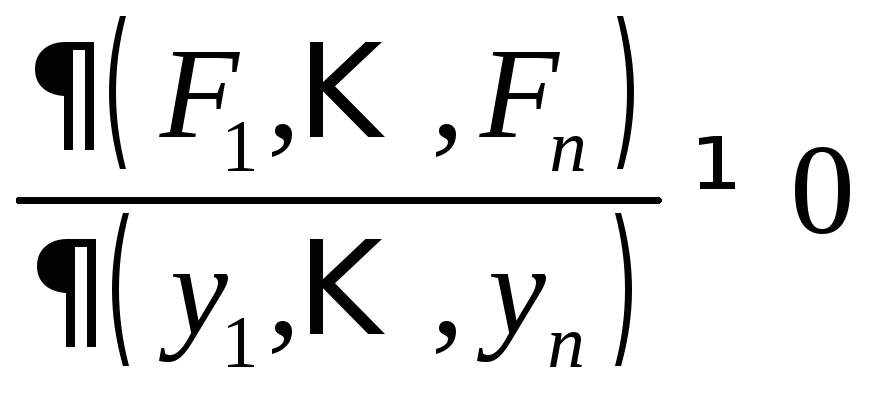 в точке
в точке![]() .
.
Тогда система уравнений
![]()
однозначно
определяет в некоторой окрестности
точки
![]() систему дифференцируемых функций
систему дифференцируемых функций
![]() ,
,![]() ,
,
удовлетворяющих
системе уравнений
![]() и начальным условиям
и начальным условиям
![]() ,
,![]() .
.
Дифференциалы этих неявных функций могут быть найдены из системы
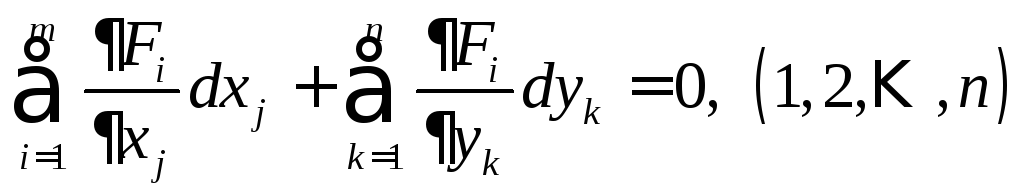 .
.
Пример 6.1.
Найти в точке (1;1) частные производные
функции
![]() ,
заданной неявно уравнением
,
заданной неявно уравнением
![]() .
.
Решение.
Из уравнения найдем значение функции
![]() в данной точке:
в данной точке:
![]() .
Функция
.
Функция
![]()
![]() равна нулю в точке (1;1;2) и непрерывна в
ее окрестности, а ее частные производные
равна нулю в точке (1;1;2) и непрерывна в
ее окрестности, а ее частные производные
![]()
также непрерывны,
![]() .
.
Поэтому функция
![]() является непрерывно дифференцируемой
в окрестности точки (1;1;2) и ее частные
производные можно найти по формулам:
является непрерывно дифференцируемой
в окрестности точки (1;1;2) и ее частные
производные можно найти по формулам:
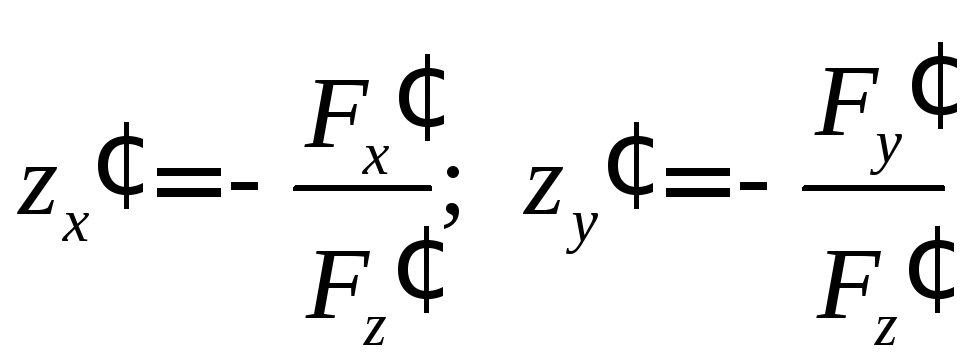 .
.
Тогда
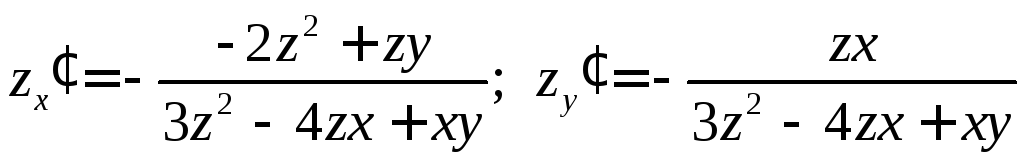 ,
,
а значение в точке (1;1;2):
![]() .
.
Пример 6.2. Найти
производные первого и второго порядков
неявных функций
![]() в точке
в точке![]() ,
если эти функции заданы системой
уравнений
,
если эти функции заданы системой
уравнений
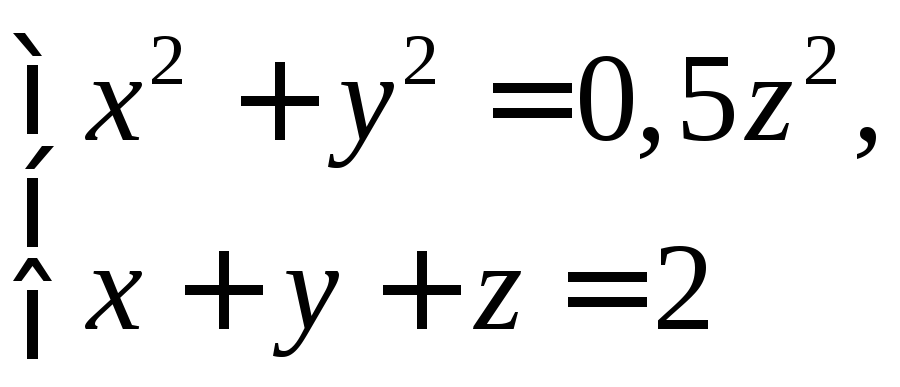 (1)
(1)
и удовлетворяют
условиям
![]() .
.
Решение. Функции
![]() и
и ![]()
дифференцируемы
в окрестности точки
![]() .
Частные производные
.
Частные производные
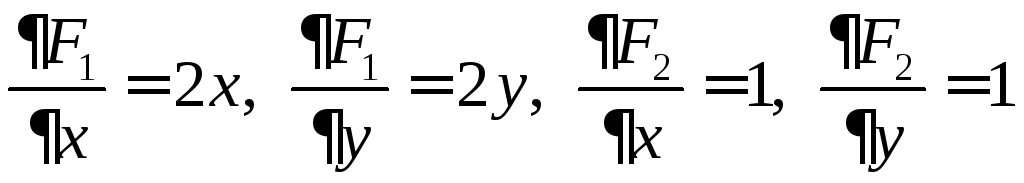
непрерывны в точке
![]() .
Так как
.
Так как![]() и
и ![]() ,
а якобиан в точке
,
а якобиан в точке
![]() отличен от нуля, т. е.
отличен от нуля, т. е.
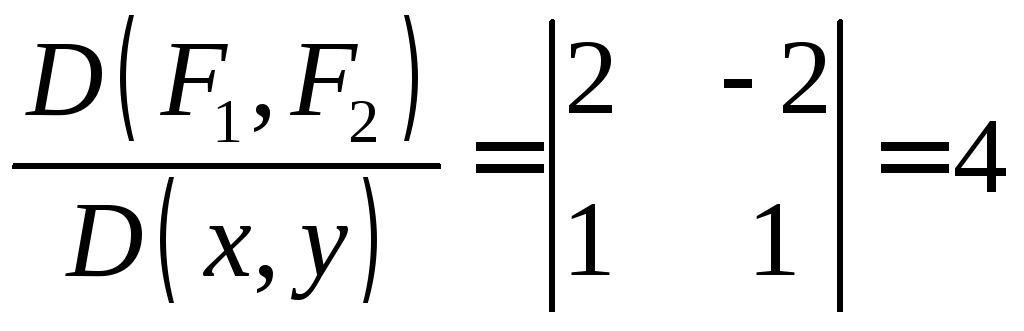 ,
,
то система уравнений
(1) определяет единственную пару функций
![]() ,
дважды дифференцируемых в окрестности
точки
,
дважды дифференцируемых в окрестности
точки![]() .
.
Продифференцируем
систему (1) по переменной
![]() :
:
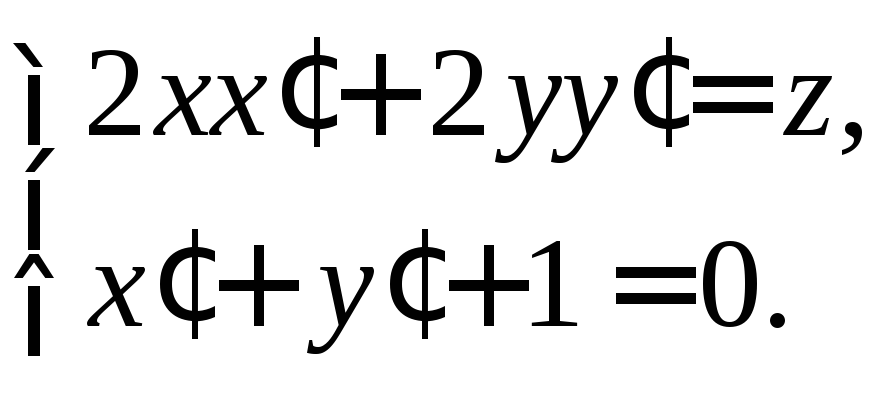 (2)
(2)
Подставив координаты
точки
![]() в эту систему, получим
в эту систему, получим
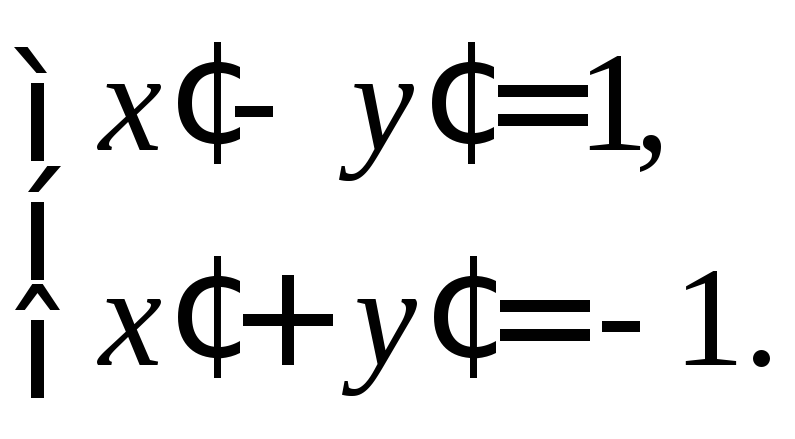
Тогда
![]() .
Еще раз продифференцируем по
.
Еще раз продифференцируем по![]() систему (2):
систему (2):
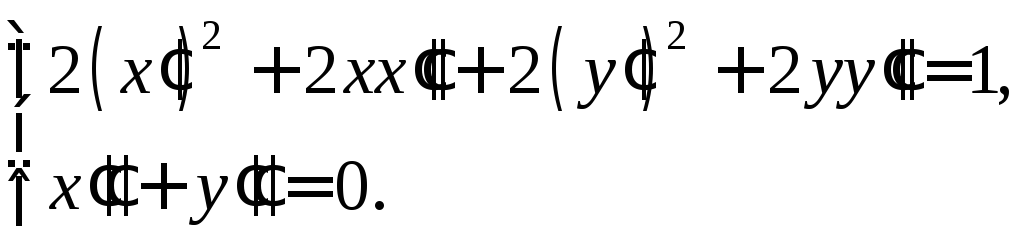
В точке
![]() имеем
имеем
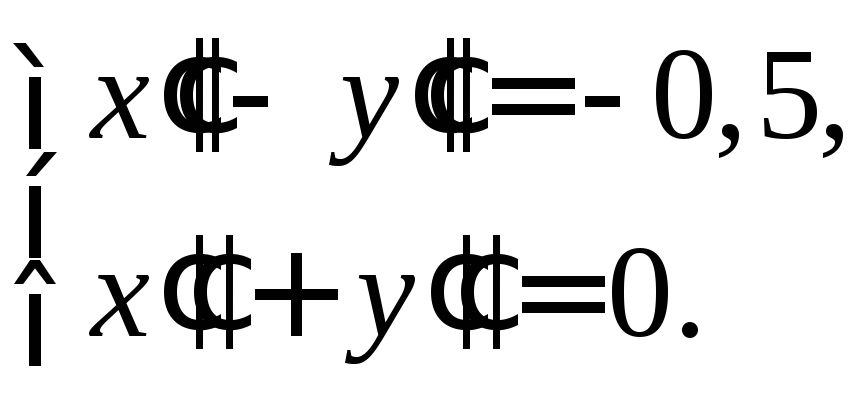
Тогда
![]() .
.
6.1.
Уравнение
![]() определяет
определяет![]() как многозначную функцию от
как многозначную функцию от![]() .
В каких областях эта функция: 1) однозначна,
2) двузначна, 3) трехзначна, 4) четырехзначна?
Определить точки ветвления этой функции
и ее однозначные ветви.
.
В каких областях эта функция: 1) однозначна,
2) двузначна, 3) трехзначна, 4) четырехзначна?
Определить точки ветвления этой функции
и ее однозначные ветви.
Найти
![]() и
и![]() для функций, определяемых следующими
уравнениями:
для функций, определяемых следующими
уравнениями:
|
6.2.
|
6.3.
|
6.4. Доказать, что для кривой второго порядка
![]()
справедливо равенство
 .
.
Для функции
![]() найти частные производные первого и
второго порядков, если:
найти частные производные первого и
второго порядков, если:
|
6.5.
|
6.6.
|
6.7.
Найти
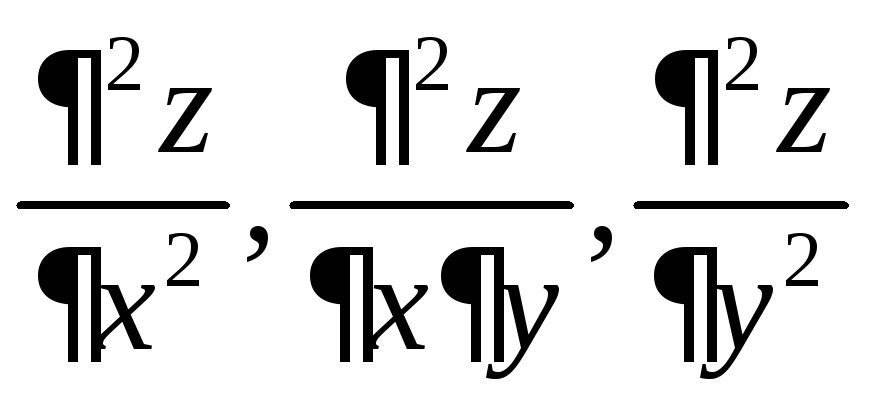 при
при![]() ,
если
,
если
![]() .
.
Найти
![]() и
и![]() ,
если:
,
если:
|
6.8.
|
6.9.
|
6.10.
Найти
![]() ,
если
,
если![]() .
.
6.11.
Найти
![]() ,
если
,
если![]() .
.
6.12.
Найти
![]() и
и![]() ,
если
,
если![]() .
.
6.13.
Найти
![]() и
и![]() ,
если
,
если![]() ,
,![]() .
.
6.14. Система уравнений
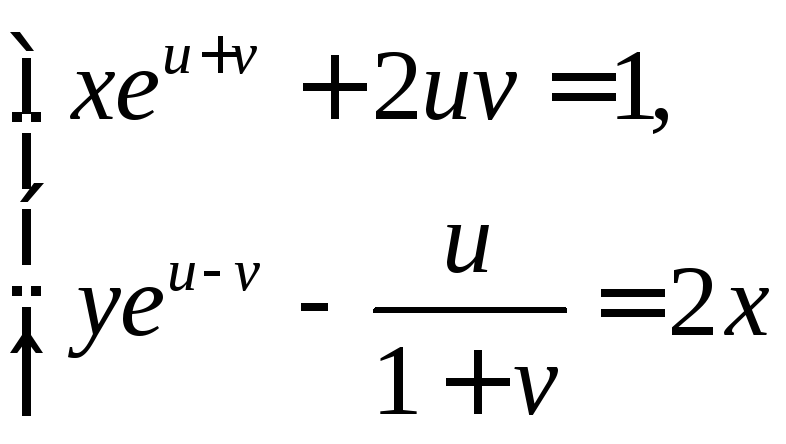
определяет
дифференцируемые функции
![]() и
и![]() такие, что
такие, что![]() и
и![]() .
Найти
.
Найти![]() и
и![]() .
.
6.15.
Функция
![]() задана уравнением
задана уравнением
![]() .
.
Показать, что
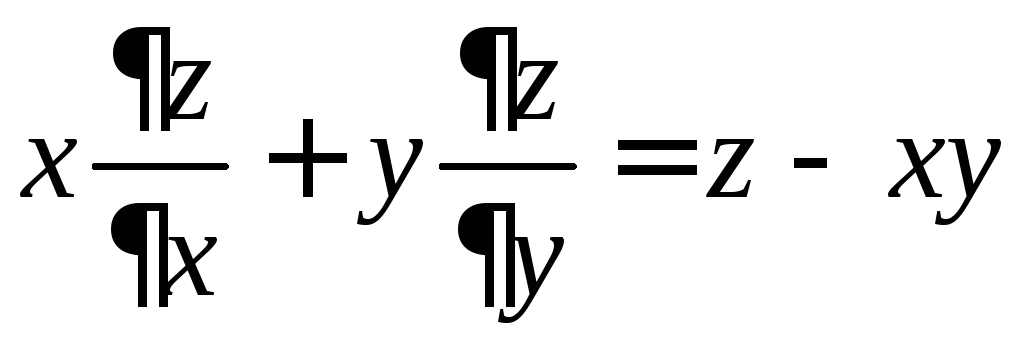 .
.
Ответы: 6.1. 1)
нигде; 2)
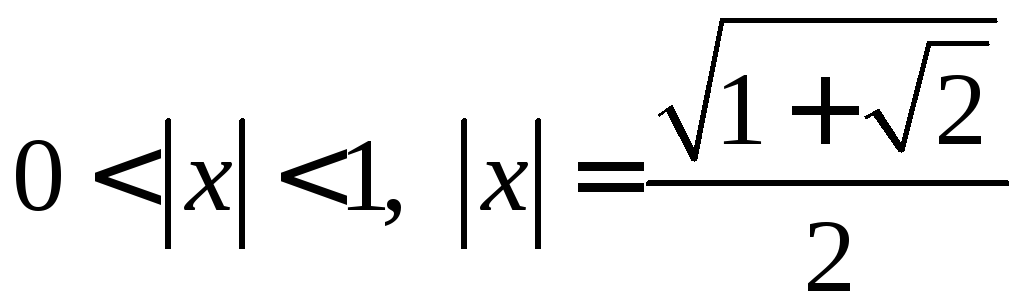 ;
3)
;
3)![]() ;
4)
;
4) 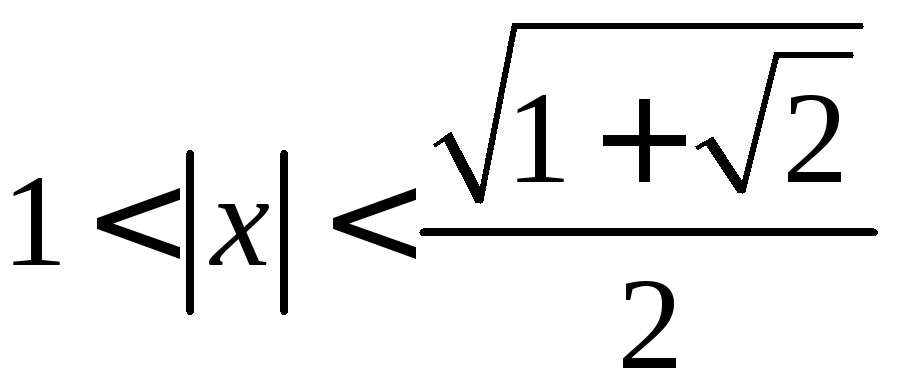 ;
однозначные ветви:
;
однозначные ветви: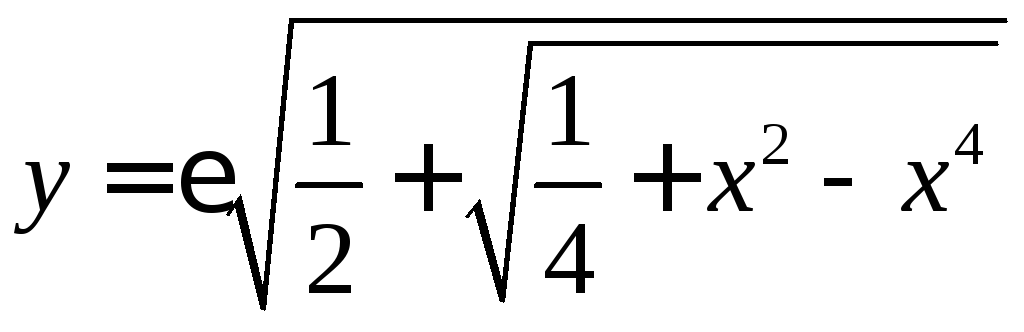 ,
,
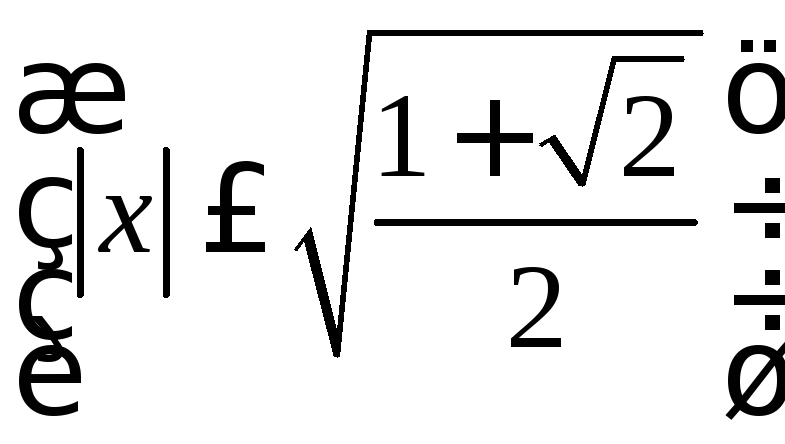 ;
;
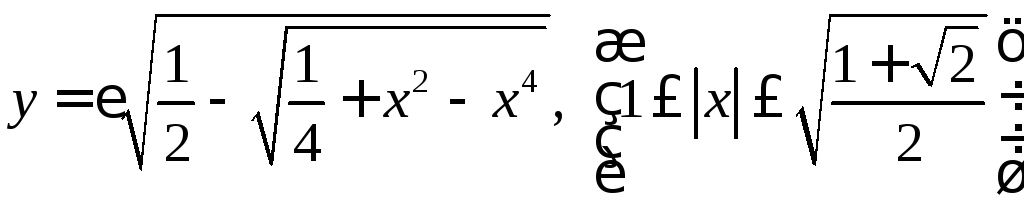 ,
где
,
где![]() .
6.2.
.
6.2. 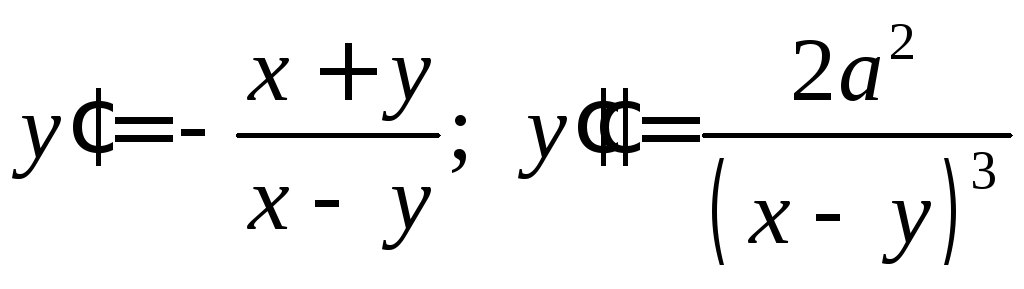 .
6.3.
.
6.3.
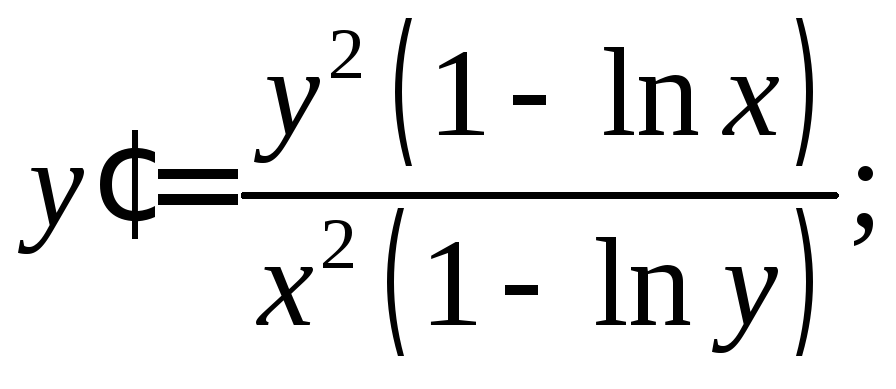
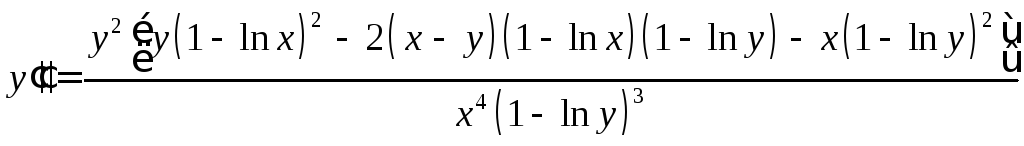 .
.
6.5.
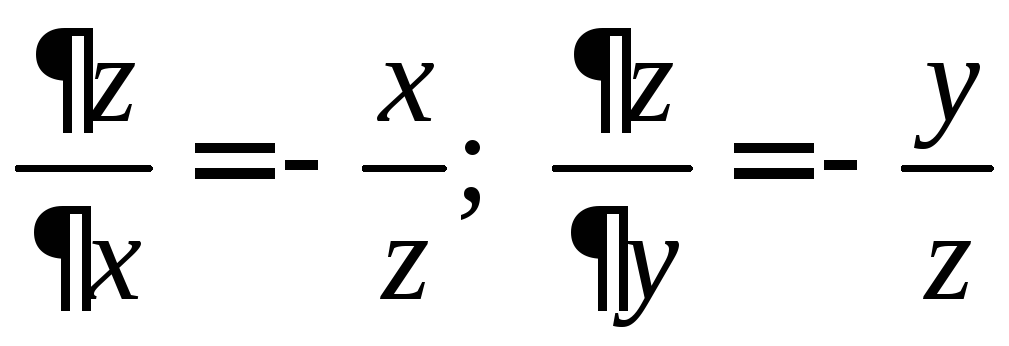 ;
;
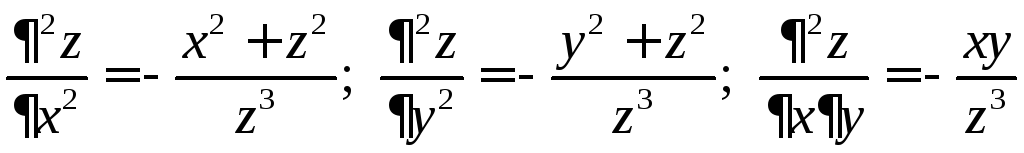 .
6.6.
.
6.6. 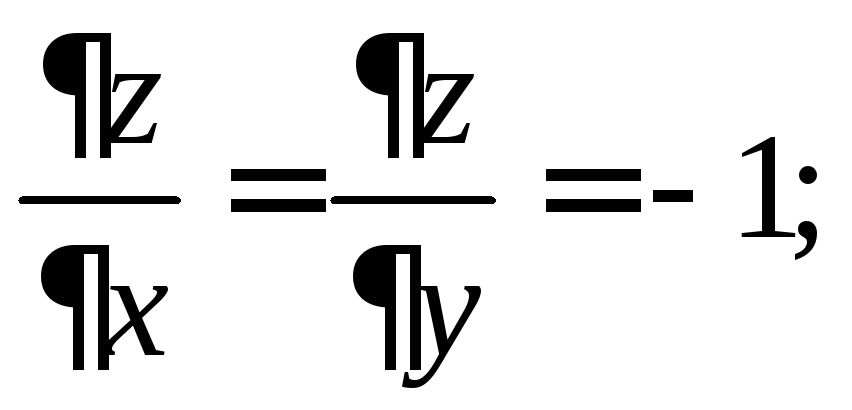
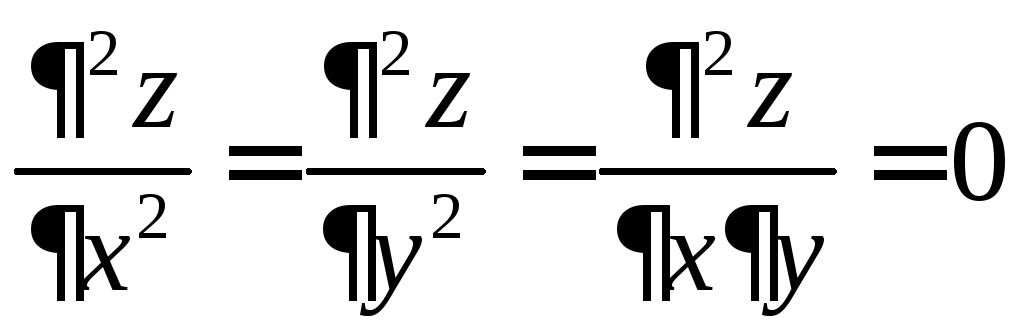 .
.
6.7.
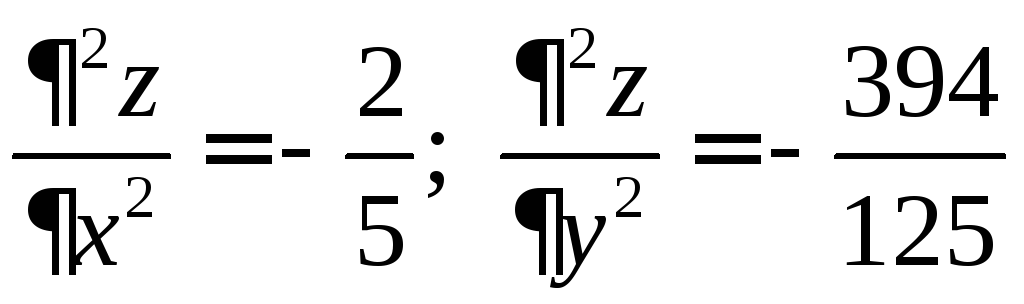 ;
;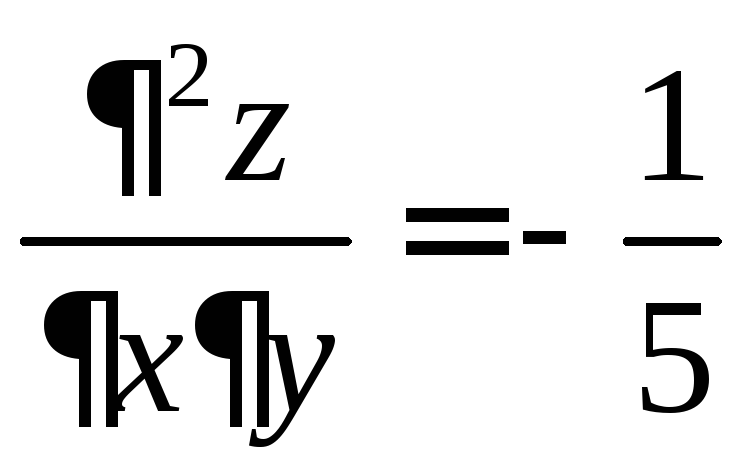 .
.
6.8.
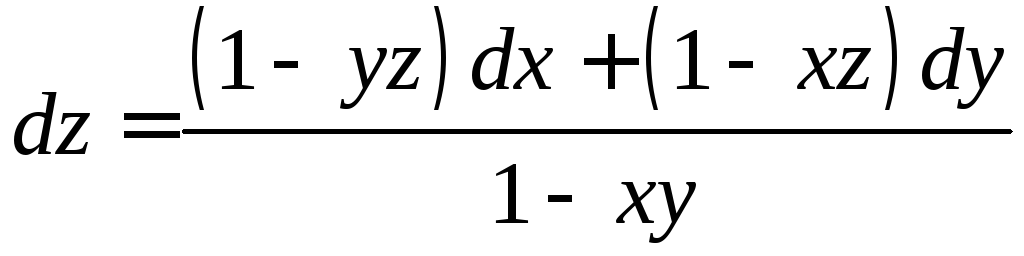 ;
;
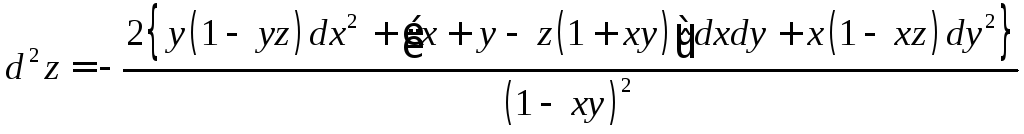 .
.
6.9.
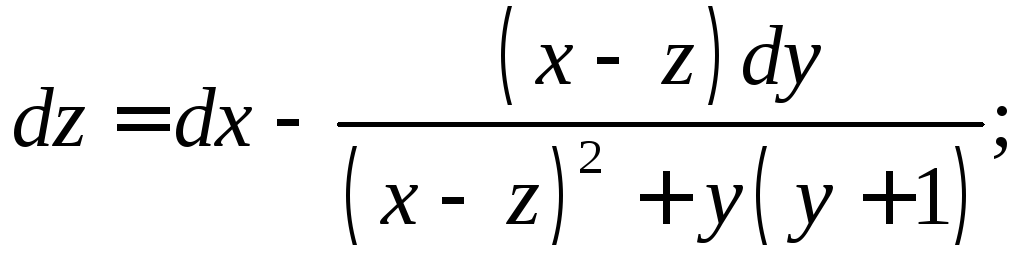
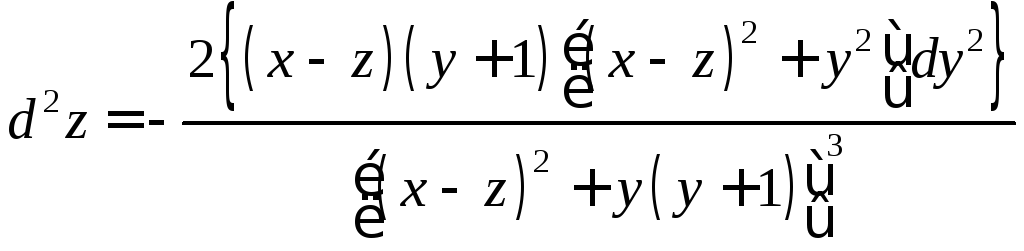 .
.
6.10.
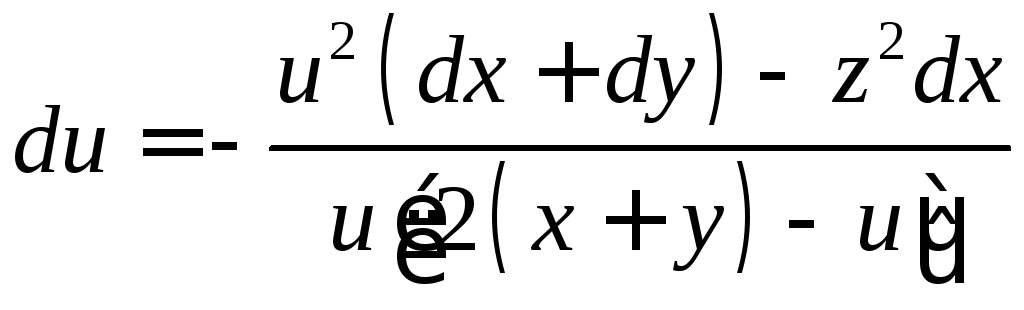 .
.
6.11.
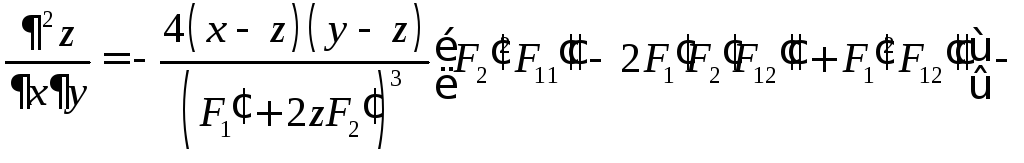
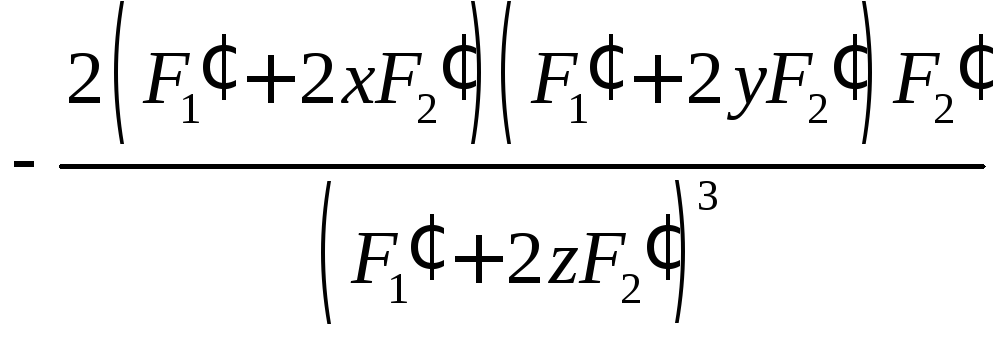 .
6.12.
.
6.12.
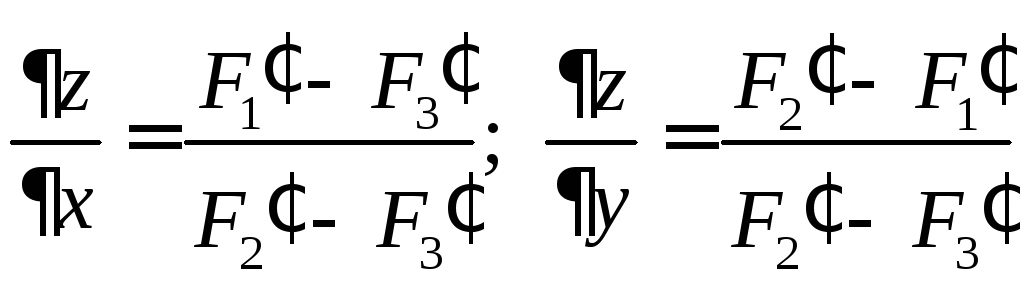 .
.
6.13. 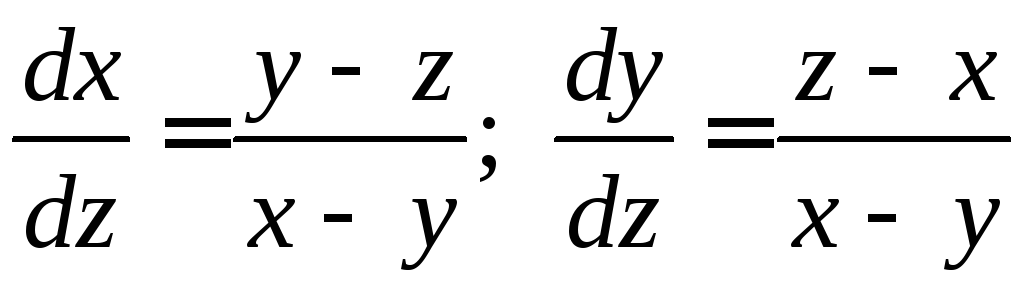 .
6.14.
.
6.14.
![]() .
.
